基于非线性能量吸振器的高耸结构减振分析

陈 勇，徐 羿

(浙江大学 结构工程研究所,杭州 310058)

高耸结构受风、地震等动力荷载作用后,会引起结构动力响应,而通过在结构上加装吸振器可以有效地抑制结构的振动[1]。吸振器的思想最早来源于1909年Frahm[2]的研究。然而传统线性吸振器(例如TMD)的适用频带较窄,只有多个吸振器联合作用才能实现多模态控制。而利用非线性吸振器的宽频吸振特性进行减振,只需有限个吸振器即可达到较好的减振效果,使得其优化参数较易确定,因此受到了研究者的关注。

Roberson等[3]提出了采用非线性吸振器进行振动控制,Vakakis将一种含有硬化立方非线性刚度的新型非线性吸振振子命名为“非线性能量阱”(Nonlinear energy sink,NES),并详细分析了其作为吸振器的潜在价值[4],即不但具有宽频减振的特性,特定情况下还具有单向输送能量并耗散的特征。Gourdon等[5]通过数值计算验证了该现象并指出NES优于传统的线性窄带吸振装置。Georgiades[6]研究了简支梁连接一个或多个NES后的横向振动问题。Georgiades等[7]研究了悬臂梁连接一个单自由度NES振子后的一维轴向振动问题,并采用有限元方法进行数值模拟验证了NES的有效性。McFarland等[8]首先设计制作了实物意义上的NES振子,该振子通过拉紧的弦的几何非线性来实现硬化立方非线性刚度。Kerschen等[9]利用其进行了一个具有两个自由度的主系统的单个NES减振研究；Nucera等[10]将其应用于多层框架结构一维振动的减振试验。这些试验及理论分析中的主结构往往具有较少的自由度。

本文对采用NES吸振器的高耸结构振动抑制特性进行了分析。该系统可简化为一个悬臂梁-NES系统。通过建立相应的偏微分运动方程,并应用伽辽金法及Rauscher方法,获得了非线性模态的解析解,揭示了NES振子吸振的原理。建立了基于有限元的离散非线性动力方程,提出了基于增量Newmark-β法的时程分析求解策略。再通过有限元分析,对该系统的振动特性随NES振子各个参数的变化进行了研究。研究结果揭示了存在最优的振子参数使得悬臂梁的振动得到最大抑制。文中最后给出了这些最优参数的估计方法。

1 运动方程

图1 安装在高耸结构上的NES振子

图2 图2 简化模型

系统的运动方程

(1a)

(1b)

式中:β*是悬臂梁的阻尼系数，δ是狄拉克函数，F*是外部激励。

将式(1)无量纲化后,可得系统无量纲运动方程为

(2a)

(2b)

式中:

(3)

2 非线性模态分析

不失一般性,考虑一根无阻尼梁,并在梁自由端作用一个简谐激励F0cosΩt,可据此获得该非线性系统的非线性模态。在出现非线性模态特征时,可采用伽辽金法将该非线性系统中梁的振动在无NES时梁的前两阶模态坐标系上近似展开:

w(x,t)=r2[u1(t)Φ1+u2(t)Φ2]

(4)

Φi(α)εK{η-[Φ1(α)u1+Φ2(α)u2]}3

(5)

(6)

根据Rauscher[12]的方法,首先考虑NES的自由振动方程

(7)

则该方程的解为

(8)

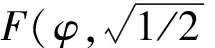
令外部激励项εf0cosΩt=εf0g(φ)。这里g(φ)又近似地展开为傅里叶级数[13],利用三倍角函数,与η有关的幂级数表示如下[14-16]。

(9)

因此,可得到一个伪自治动力系统：

Φi(α)εK{η-[Φ1(α)u1+Φ2(α)u2]}3

(10)

(11)

令

考虑到

把式(11)代入式(10)可得

Φi(1)f0g(φ)+Φi(α)Kη3+O(ε)

(12)

将η=ηmax代入式(12),得到边界条件下的方程

(13)

则系统的解可表示为

(14)

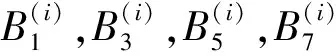
为验证式(14)的结果,采用龙格库塔法进行数值模拟。令系统(5)和(6)的参数为

ε=0.1,f0=0.1,K=2,M=1,

Ω=0.588 502,ηmax=0.5,α=0.783

(15)

且初始条件为

(16)

将数值模拟结果与式(14)的结果比较如图3所示,可见两者较为吻合,说明式(14)可很好地表征系统的非线性模态。通过对模态形状的分析可发现,可发现u1比η小了100倍，即振子的振幅远大于悬臂梁的模态振幅。表明该振子在出现非线性模态时能较好地吸收系统的能量。

图3 非线性模态

3 非线性有限元时程分析

3.1 非线性时程分析

利用有限单元法可建立系统的离散非线性运动方程

(17)

式中:阻尼矩阵C由各阶模态阻尼比获得，M和K分别为质量矩阵和刚度矩阵。为了较好地描述悬臂梁振动特性,质量矩阵采用了一致质量阵。式(17)中的X是位移向量,即:

X=[w1…wNES…wnq]T

(18)

其中:n为主系统的自由度数。F为外荷载向量，FN由NES的回复力引起,为

FN=[0 …FR… 0 -FR]T

(19)

其中：FR=K(q-wNES)3，wNES为梁上连接NES位置的竖向位移。

考虑到采用增量形式的Newmark-β法[11]在求解非线性时程中具有较高的可靠性,因此本文给出了基于该方法的求解策略,用于计算含NES振子的系统的动力响应。

(20)

其中:KR=K(q-wNES)2。则新的系统运动方程

(21)

线性化后的式(21)则可采用增量Newmark-β法计算下一时间步的位移。由于该位移会致使KL的值发生变化,故该位移还不是非线性系统下一时间步的精确解。可利用该位移对应的KL并结合Newton插值法计算新的KL(需注意到KL恒大于零),回代入式(21),再利用增量Newmark-β法进行下一时间步位移的计算。如此反复迭代,直至下一时间步的位移和KL匹配为止,即迭代收敛。收敛准则为: ① 计算KL的当前值与上一次值的差值；② 该差值的绝对值与KL上一次值的比值小于一个较小的数μ(精度)。图4给出了具体计算过程的流程图。

图4 计算过程流程图

3.2 非线性能量阱参数敏感性分析及经验公式

(22)

图5 窄带白噪声集中激励F0

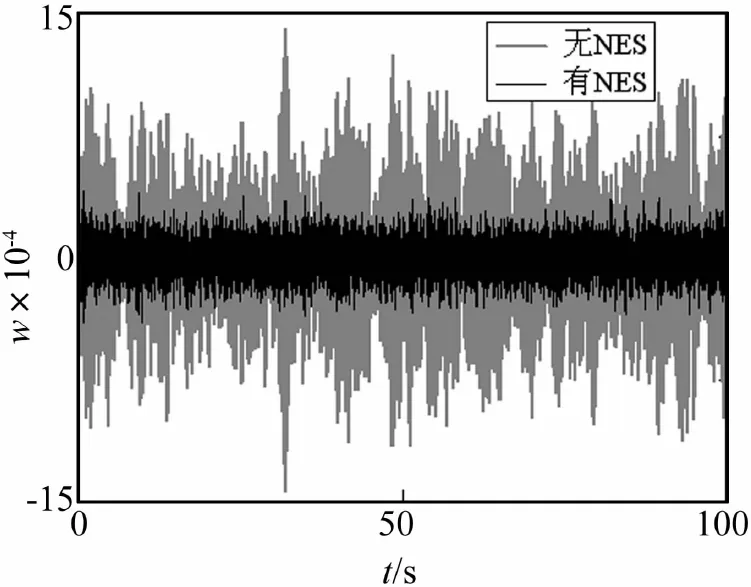
图6 悬臂梁自由端的位移时程

图7 悬臂梁自由端位移的功率谱

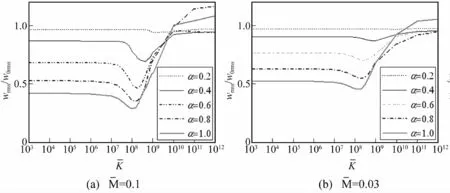
图8 悬臂梁自由端位移的均方根随NES刚度变化

图9 悬臂梁自由端振幅均方根随NES质量变化

图10 悬臂梁自由端振幅均方根随NES阻尼变化

图11 随阻尼变化

图12 随外荷载变化

(23)

(24)

(25)

(26)

式中:log-1(·)指以10为底的对数函数的逆函数。

图13 荷载归一化的6opt随质量变化

图14 数值分析与式(26)结果对比

4 结 论

将NES用于高耸结构的减振研究结果表明：

(1)连接NES后的系统非线性特征突出,非线性模态分析结果显示在出现非线性模态时,模态分析表明梁位移比NES位移小了两个数量级,表明NES可有效吸收结构振动。

(2)给出了可应用于含NES结构的非线性有限元时程分析方法。利用其对在窄带白噪声集中激励作用下的系统减振特性进行了参数分析。结果表明,在选择适当的NES参数值后,NES可降低梁端振幅均方根值80%左右。

(3)给出了与结构振动特征和荷载大小相关的NES参数选择方法,并提出了工程意义上的NES最优刚度的经验公式。

[1]Nagaya K，Kurusu A，Ikai S，et al.Vibration control of a structure by using a tunable absorber and an optimal vibration absorber under auto-tuning control[J].Journal of Sound and Vibration，1999，228(4): 773-792.

[2]Frahm H.Vibrations of bodies[P].USA，989958.1911-04-18.

[3]Roberson R E.Synthesis of a nonlinear dynamic vibration absorber[J].Journal of the Franklin Institute,1952,254(3): 205-220.

[4]Vakakis A F.Inducing passive nonlinear energy sinks in vibrating systems[J].Transactions-American Society of Mechanical Engineers Journal of Vibration and Acoustics,2001，123(3): 324-332.

[5]Gourdon E，Lamarque C H.Energy pumping with various nonlinear structures: Numerical evidences[J].Nonlinear Dynamics,2005，40(3): 281-307.

[6]Georgiades F.Nonlinear localization and targeted energy transfer phenomena in vibrating systems with smooth and non-smooth stiffness nonlinearities[D].Athens，Greece: National Technical University of Athens，2006.

[7]Georgiades F，Vakakis A F，Kerschen G.Broadband passive targeted energy pumping from a linear dispersive rod to a lightweight essentially non-linear end attachment[J].International Journal of Non-Linear Mechanics，2007，42(5): 773-788.

[8]Mcfarland D M，Bergman L A，Vakakis A F.Experimental Study of Non-Linear Energy Pumping Occurring at a Single Fast Frequency[J].International Journal of Non-Linear Mechanics,2005，40(6): 891-899.

[9]Kerschen G，Kowtko J J，Mcfarland D M，et al.Theoretical and experimental study of multimodal targeted energy transfer in a system of coupled oscillators[J].Nonlinear Dynamics，2007，47(1): 285-309.

[10]Nucera F，Lo Iacono F，Mcfarland D M，et al.Application of broadband nonlinear targeted energy transfers for seismic mitigation of a shear frame: experimental results[J].Journal of Sound and Vibration，2008，313(1): 57-76.

[11]Clough R W，Penzien J.Dynamics of structures[M].New York: McGraw-Hill，1993.

[12]Rauscher M.Steady oscillations of systems with non-linear and unsymmetrical elasticity[D].Cambridge，Massachusetts，USA: Massachusetts Institute of Technology，1937.

[13]Avramov K V，Mikhlin Y V.Snap-through truss as an absorber of forced oscillations[J].Journal of Sound and Vibration，2006，290(3): 705-722.

[14]Whittaker E T，Watson G N.A course of modern analysis[M].Cambridge，UK: Cambridge University Press，1996.

[15]Byrd P F，Friedman M D.Handbook of elliptic integrals for engineers and scientists[M].Berlin: Springer-Verlag，1971.

[16]Kiper A.Fourier series coefficients for powers of the jacobian elliptic functions[J].Mathematics of Computation,1984，43(167): 247-259.