基于小波变换的反射波法基桩检测

张敬一, 陈龙珠

(上海交通大学 船建学院安全与防灾工程研究所，上海 200240)

桩基检测技术中低应变反射波法以检测快捷、成本低、效果好获得到广泛应用[1]。但其在应用中存在一定局限性。对从桩顶传至桩底再反射回桩顶的反射波信号，当基桩长径比过大、桩侧土剪切模量较高时，桩底反射波到达桩顶的能量所剩无几；在桩身微小缺陷处阻抗变化太小以致反射波亦较微弱。对在役基桩桩顶有梁、板、承台等平台而采用平台激振方式时，上部结构的存在会引起信号明显的三维效应，波形表现为低频大摆动形态；激振后应力波在平台上下界面及四周边界的反射也会形成干扰信号，使透射到桩身的应力波能量减少，反射波亦较微弱。由此知，顶部裸露自由桩受长径比、桩周土剪切模量、缺陷面积大小影响，若桩底或缺陷处反射太弱而不足以有效识别；而对桩顶非裸露自由桩，干扰成分的存在影响对桩底反射波的识别。因此，低应变反射波法的应用受到一定限制，其检测结果的可靠性也会受影响。

小波变换[2-3]又称“数学显微镜”，为良好的时频域分析方法，且具有多分辨率分析特点，适用于基桩检测中桩底或缺陷等奇异成分的探测。将小波变换用于处理反射波信号，不仅可将干扰信号与桩底或缺陷反射在不同频带内显示，减小干扰成分影响，而且可探测信号中微弱的桩底或缺陷反射波。

针对低应变反射波法在基桩检测中的缺点，本文通过建立三维轴对称有限元模型，分析并讨论桩基检测中桩长径比、桩周土剪切模量、缺陷面积大小、桩顶非裸露等因素影响及局限性；通过对反射波信号进行小波变换，对比分析小波变换对波形的改善，验证小波变换在桩基检测反射波信号分析中的有效性。

1 小波变换与小波基选取

Daubechies小波为有限紧支撑的正交小波，时频域局部化能力较强。其中小波族的光滑性、局部性良好，且连续可微，适合瞬态信号中奇异性位置确定[4]。消失矩N=9时，小波函数及尺度函数的频率特性已很好，时域分辨率满足要求，故选db9小波进行分析。

以桩顶有平台的高桩形式为例，在平台顶激振。对地基土剪切波速150 m/s的完整桩，其平台顶反射波信号小波波形见图1。图中cd0为反射波信号，cd1～ cd8为小波分量。在反射波信号cd0中，由于微弱的桩底反射与低频大波动干扰成分叠加，难以有效判断桩底反射波的到达。而cd0的波谷并非桩底反射波，为由低频大波动引起。小波变换后将二者有效分离，桩底反射波成分体现在cd3小波分量中，而低频大波动成分则呈现在cd6～cd8中。图1中箭头为桩底反射的理论达到时间，与识别的桩底反射到达时间吻合较好。由此可见，db9小波基适用于低应变反射波信号分析。

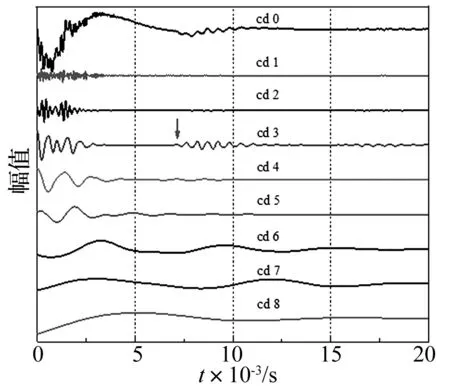
图1 反射波信号及小波变换

2 桩-土体系有限元模型

图2 桩-土系统示意图

用通用有限元软件ABAQUS建立三维轴对称有限元模型，模型计算区域45 m×8 m，在侧边、底边分别采用无限元作为吸收边界，以降低从有限元区域边界产生虚假反射波影响[5]，模型示意图见图2。桩-土体系采用4节点轴对称实体单元。由于在基桩低应变动测中激振能量较小，故忽略桩土间接触，桩、土均采用线弹性本构模型[6]。桩波速取3 800 m/s，为能准确模拟波的传播，最大单元尺寸应小于380tc/ 2.5[7]，将桩与土的有限单元尺寸均取0.03 m。桩直径0.4 m，桩长L，计算参数见表1。P波、S波波速分别记为Vp，Vs，其表达式为：

(1)

(2)

式中：v为泊松比；E为弹性模量；ρ为质量密度；G为剪切模量。

数值模型用中央差分法计算桩顶面质点振动速度时程信号。为减小三维效应影响，反射波信号均由距桩中心0.12 m处检波获得。竖向激振力作用于桩顶面中心，用半正弦集中荷载[8]：

(3)

其中：P0=1 N；激振力持续时间tc=0.001 s。

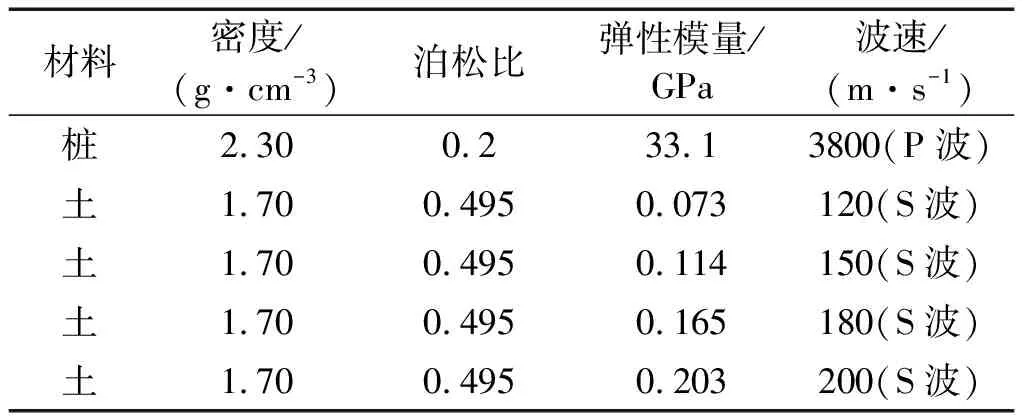
表1 桩-土参数选取

3 顶部裸露自由桩小波变换

低应变反射波法虽适用顶部裸露自由桩检测，而桩长径比与地基土剪切模量为P波能量耗散的主要因素[9]，且缺陷面积大小与反射波在缺陷界面反射能量成正比。当桩长径比太大、桩周土剪切模量太高、或桩身缺陷面积太小、实测信号中存在环境噪声时，桩底或缺陷反射波因到达桩顶时的能量较微弱而不足以有效识别。而小波变换有探测信号中奇异成分能力，故可用于完整桩桩底深度与缺陷桩微小损伤探测。

3.1 完整桩检测

完整桩桩底深度检测主要受长径比及桩周土剪切模量影响。不同组合条件下，反射波信号见图3，箭头处为理论桩底反射时间。桩长径比为25时，有效识别桩底反射波地基土剪切波速不宜超过180 m/s；长径比50、地基土剪切波速120 m/s时可见较弱的桩底反射波。此与文献[10]结论一致。对图3中信号进行小波变换，取其中cd 3波形见图4。当桩长径比为25、50、75时，信号中能识别桩底反射波对应的最大地基土剪切波速为200 m/s、150 m/s、120 m/s。不同桩长径比对应的最大地基土剪切波速分析结果见图5。由图5看出，反射波信号小波变换适用的最大长径比与地基土剪切波速明显提高，在一定程度上可减小桩长径比与地基土剪切波速的限制。两曲线与坐标轴间区域为反射波法及小波变换后各自适用的检测范围，而两曲线间区域即小波变换拓展的检测区域。实测信号中会有环境噪声干扰，而小波变换亦有较好去除环境噪声干扰作用。

图3 不同长径比地基土剪切波速信号

图4 不同桩长径比地基土剪切波速小波波形

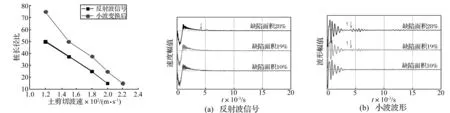
图5 反射波法及小波变换后适用最大土剪切波速与长径比

3.2 缺陷桩检测

沿桩身向下传播的应力波会在缺陷等阻抗变化处反射。当桩身缺陷太小时，由于桩阻抗变化小,缺陷反射微弱较难识别，而其对承载力影响不可忽视。为进一步研究反射波法对缺陷桩微小缺陷的识别，20 m桩长，在8 m处存在缺陷面积分别为28 %、19 %、10 %等不同程度的缩颈，缺陷长度0.5 m，地基土剪切波速150 m/s，反射波信号及cd 3小波波形见图6，图中箭头为缺陷反射的理论时间，与信号中桩底反射波位置较一致。当缺陷面积为28%时，从反射波信号中尚能勉强识别缺陷反射；当缺陷面积减小到19 %或10 %时，已无法识别桩底反射到达。此与缺陷面积达30 %时才能有效识别缺陷[7]的结论基本一致。经信号小波变换后(图6(b))，可对缩颈19 %的缺陷识别、定位，对缩颈10 %的信号虽可判断桩身存在轻微损伤，但定位有一定误差。可见，小波变换有利于识别反射波信号中无法识别的桩身缺陷，最小可识别缺陷面积由28%减小至19%。

4 顶部非裸露自由桩小波变换

低应变反射波法主要用于在建工程桩等桩顶裸露自由情况，对港口码头、桥梁及工业民用建筑的在役桩中, 桩顶常与板、梁、承台等平台结构连接，使基于反射波法的无损检测面临较大困难。受上部结构四周边界反射、上下界面多次反射及各种直达波(P波、SV波、瑞利波)及三维效应影响，反射波信号中会存在较强干扰。在平台顶桩中心位置激振后，透过平台-桩顶界面的 P 波沿桩身向下传播，该部分 P 波为识别桩长与桩身完整性的有效成分。

桩顶有平台时，采用高桩形式并在平台中心激振。在轴对称模型中，桩、平台均为圆形截面，桩半径0.2 m，入土深度10 m，地上部分高度3 m，地基土 S 波速150 m/s。地下部分桩-土计算模型同图 2，地上部分见图 7。记α=a/r、β=b/r分别为平台相对半径与厚度，其中a、b分别为平台半径及厚度，r为桩半径。

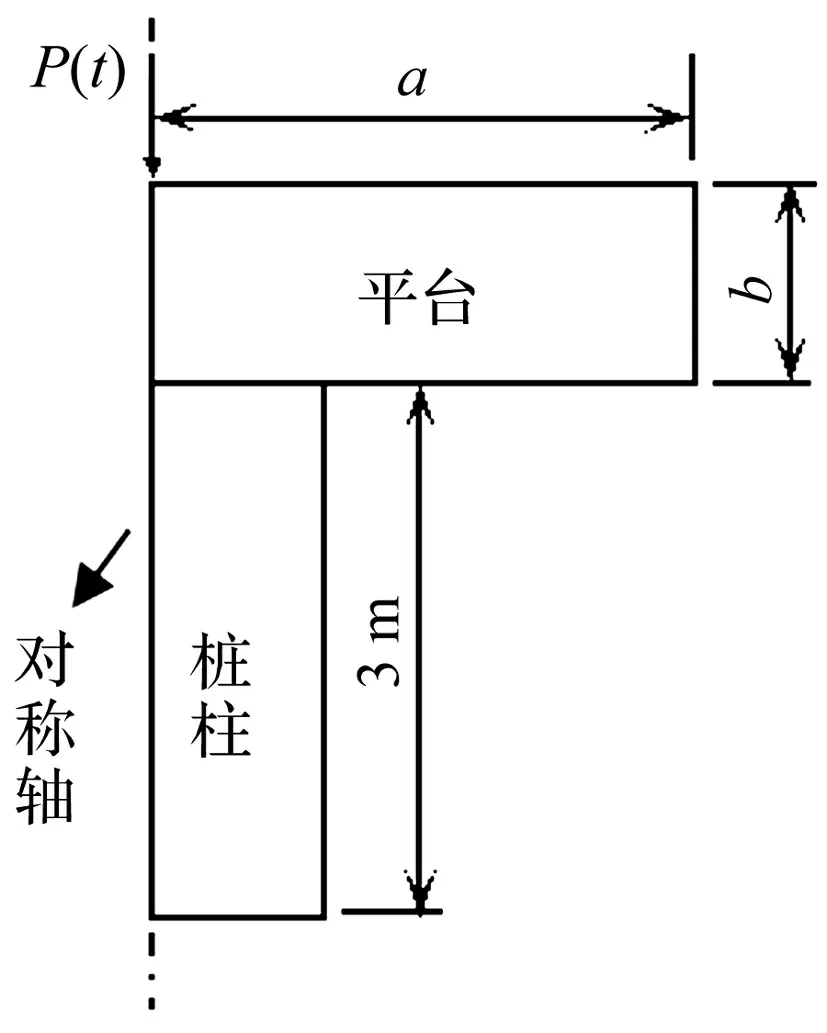
图7 桩-土系统地上部分示意图

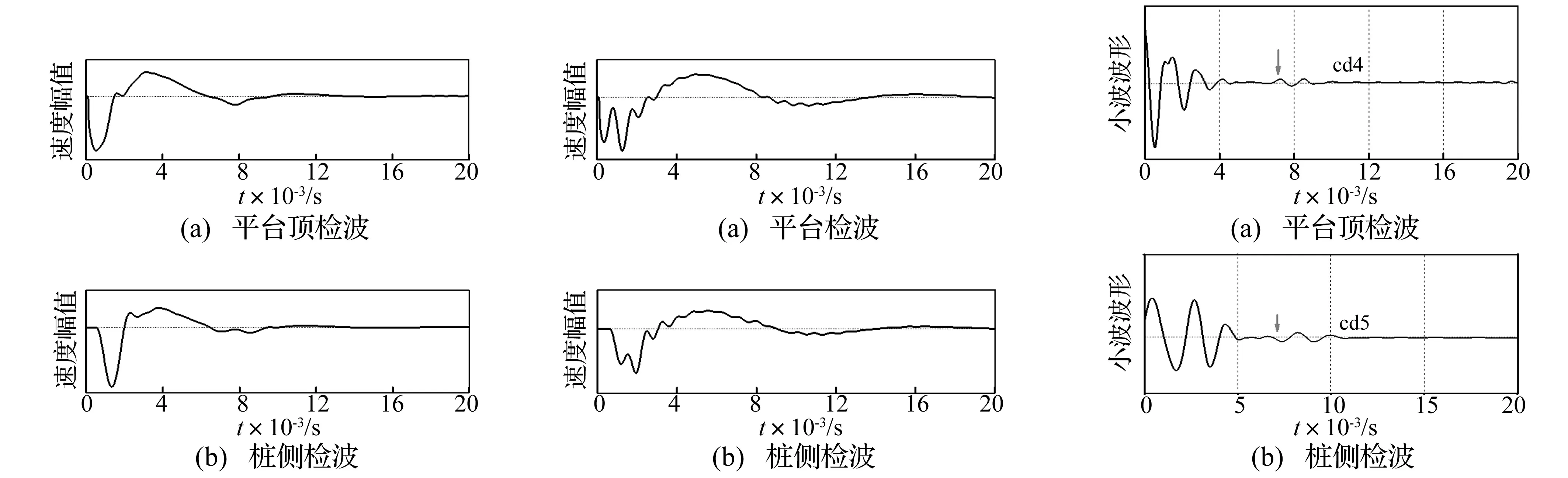
图8 桩顶非自由端时平台顶与桩侧信号(α=2，β=1)

平台半径0.4 m、厚0.2 m(α=2，β=1)时，分别在平台顶与桩侧0.5 m处接收的信号见图 8。平台作为三维体会引起信号三维效应，呈现与浅部缺陷时类似的低频大摆动特征，与桩底反射波叠加后，虽可勉强识别桩底反射，但因存在较大干扰信号，判断桩底深度会对结果产生影响。图9为α=3，β=2时的信号，平台尺寸增加后，桩底反射更微弱，与低频大波动干扰成分叠加后，更难识别桩底反射。

透射到桩身的P波能量关系到能否有效识别桩底反射，而平台厚度、半径与桩径大小为影响透射能量的关键因素[11]。平台较厚且有效面积较大时，透射的P波较少；平台较薄，桩底反射与低频大波动成分叠加后也会影响判断精度甚至误判。而小波变换的时频特性优良，既可去掉高频、低频成分干扰，亦可对微弱桩底反射放大。在cd4或cd5小波分量中可观察到桩底反射，见图10。由图10看出，桩侧检波较平台检波其桩底反射更明显。增大平台尺寸为α=5、β=4时强烈干扰已无法识别微弱的桩底反射。可见通过小波变换识别桩底反射，平台需在有效尺寸内。

改变平台尺寸，即可获得通过小波波形识别桩底反射时平台的有效尺寸(仅考虑平台截面大于桩截面情况，即a>1)，分析结果见图11。由图11中α、β关系曲线的变化趋势可见，通过小波变换有效分析反射波信号，平台相对尺寸α、β值应在相应曲线以内，且桩侧检波较平台顶检波更易识别桩底反射。无论平台顶或桩侧检波，β均随α的增大而减小，最后趋于某一定值，即当平台尺寸远大于桩径时，若在平台顶检波，则平台厚度不宜超过一倍桩半径；若在桩侧检波，平台厚度不宜超过两倍桩半径。

图11 小波变换有效确定桩底深度的平台相对尺寸

5 结 论

通过建立三维轴对称有限元模型，对模拟信号进行小波变换表明，小波变换可作为有效的桩基检测信号处理方法，结论如下：

(1) 小波变换可用于高长径比、地基土剪切模量较大等反射波法不适用的情况。对信号进行小波变换后，其适用的最大桩长径比与土剪切波速关系曲线明显提高。

(2) 小波变换能识别反射波信号中无法识别的缺陷面积达19%的反射。

(3) 桩顶有平台且在其顶部激振时，平台顶与桩侧检波信号中均存在较大干扰，会影响对桩长与完整性判断；平台在有效尺寸范围内时，小波变换可较大程度减小干扰信号影响，识别桩底反射。

参 考 文 献

[1]陈 凡, 徐天平, 陈久照, 等. 基桩质量检测技术[M]. 北京: 中国建筑工业出版社, 2003.

[2]Ni S H,Lo K F,Lehmann L,et al.Time-frequency analyses of pile-integrity testing using wavelet transform[J]. NDT & E International, 2008, 35(4): 600-607.

[3]赵燕容，袁宝远. 基于小波的时序改进法在深基坑监测中的应用[J]. 岩土力学, 2008, 29(12): 3381-3386.

ZHAO Yan-rong, YUAN Bao-yuan. A method based on time series improvement method of wavelet applied to deep foundation pit monitoring [J]. Rock and Soil Mechanics, 2008, 29(12): 3381-3386.

[4]唐颖栋, 冯元群. 基桩动测信号的小波分析[J].振动与冲击, 2010, 29(2): 131-135.

TANG Ying-dong, FENG Yuan-qun. Wavelet analysis of dynamic test signals of a pile[J]. Journal of Vibration and Shock, 2010, 29(2):131-135.

[5]Ni S H, Huang Y H, Zhou X M, et al. Inclination correction of the parallel seismic test for pile length detection[J]. Computers and Geotechnics, 2011, 38(2):127-132.

[6]Liao Shu-tao, Tong Jian-hua, Chen Cheng-hao, et al. Numerical simulation and experimental study of parallel seismic test for piles[J]. International Journal of Solids and Structures, 2006, 43(7-8): 2279-2298.

[7]Huang Y H, Ni S H, Lo K F, et al. Assessment of identifiable defect size in a drilled shaft using sonic echo method: numerical simulation[J]. Computers and Geotechnics, 2010, 37(6): 757-768.

[8]黄大治, 陈龙珠. 旁孔透射波法检测既有建筑物桩基的三维有限元分析[J].岩土力学,2008,29(6):1569-1574.

HUANG Da-zhi, CHEN Long-zhu. 3D finite element analysis of parallel seismic tests for integrity of piles of existing structures[J]. Rock and Soil Mechanics, 2008, 29(6): 1569-1574.

[9]Jung G J, Cho S M, Kim M M. Defects of drilled shaft and effects of surrounding geo-materials predicted by sonic-echo tests[C]// Proceedings of the 17thInternational Off shore and Polar Engineering. Portugal: 2007.

[10]Huang Y H, Ni S H. Experimental study for the evaluation of stress wave approaches on a group pile foundation[J]. NDT & E International, 2012, 47: 134-143.

[11]Gassman S L, Finno R J. Cutoff frequencies for impulse response tests of existing foundations[J]. Journal of Performance of Constructed Facilities, 2000, 14(1): 11-21.