基于动力学模型与参数优化的ISD悬架结构设计及性能分析
2014-09-05陈轶杰王亚军张亚峰
杜 甫, 毛 明, 陈轶杰, 王亚军, 张亚峰
(中国北方车辆研究所,北京 100072)
悬架系统性能对车辆平顺性、操稳性、安全性有直接影响。弹簧与阻尼器并联的悬架结构至今已有百年历史,未改进。直至Smith等[1-2]提出无接地要求的惯性元件-惯容器,才探索出改善悬架性能的新途径。
如何发挥惯容器作用,设计结构简单、性能优越的ISD悬架为该领域研究重点。主要方法为:① 用机电相似性理论,据惯容器与电容对应、弹簧与电感对应、减振器与电阻对应,将I(惯容器),S(弹簧),D(减振器)作为电气元件设计悬架的拓扑结构。该方法理论上可行,但滤波电路结构形式相对固定,仅系统阶数、元件参数不同[3-4],且惯容器及阻尼元件具有不能单独承受静载的特殊要求,直接套用滤波电路综合方法设计的悬架结构在工程上不一定可行。② 将悬架设为“黑箱”,推导满足悬架性能要求的传递函数,用物理元件进行综合。但同一传递函数构建的悬架结构并不唯一,且设计的新结构同样有被“击穿”的可能。对此,陈龙等[5-6]借鉴电学中级联滤波思想,据机械系统实际进行改进,创建两级串联型ISD悬架;对惯容器、弹簧、阻尼任意二元件间串并联结构在单自由度系统中的频响及振动传递动态特性进行对比研究,提出二元件连接的理想匹配关系,并创建性能优越、结构简单的ISD悬架。以上方法构建了性能优越ISD悬架拓扑结构,但不具一般性及通用性。
本文提出设计ISD悬架结构的一般方法。将储能元件、支撑元件、耗能元件按排列组合方式安排在不同位置,组合工程可行悬架结构,通过建立通用动力学模型、通用频率响应显式,将簧上质量加速度均方根值与轮胎动载均方根值作为优化目标,以悬架偏频及动行程为约束条件,建立优化模型。取相同车型参数,对每种悬架结构各元件参数进行优化,对比新型结构与传统悬架的幅频特性,其中12种性能优于传统悬架,选出典型结构进行可行性分析。
1 ISD悬架拓扑结构建立
传统悬架中,弹簧为储能、承载元件,减振器为耗能元件。ISD悬架中,惯容器为新型储能元件,可缓和地面冲击。关于惯容器布置国内外均有广泛研究,文献[6]通过对比仿真已验证惯容器与弹簧在隔振布置上宜采用如图1(a)的串联形式。由于单独惯容器无承静载能力,须设置承载元件,见图1(b),可单独用弹簧K1或K2,也可同时用K1K2共3种情况。仅弹性元件及惯性元件组成的结构受冲击后会产生振动,持续振动易使乘员产生不适及疲劳,故悬架中应具有使振动迅速衰减的阻尼元件,见图1(c),含c1,c2,c3,c1c2,c1c3,c2c3,c1c2c3共7种排列形式。惯容器最通用的悬架结构(图1(c))含21种工程可行悬架拓扑结构。
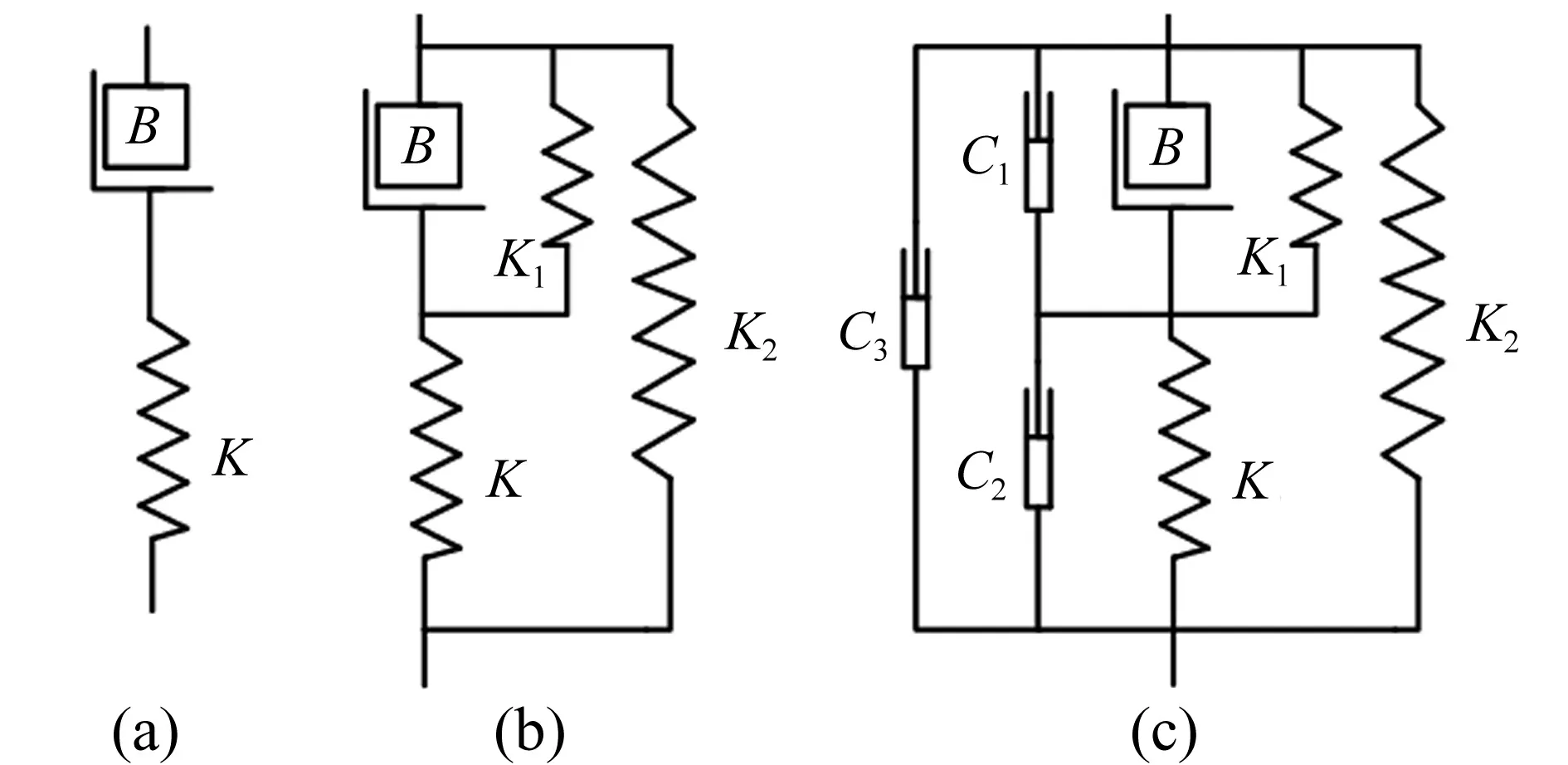
图1 ISD悬架模型构建步骤示意图
2 通用动力学模型
2.1 系统微分方程
以图1(c)结构为悬架,建立1/4车体振动模型,见图2[7],含上述21种ISD悬架拓扑结构的通用模型,据牛顿第二定律建立系统动力学微分方程组:
(1)

图2 ISD悬架1/4车体通用模型
式中:m1为簧下质量;m2为簧上质量;z2,z1分别为簧上、簧下质量垂直位移坐标;z为惯容器B下端与弹簧K上端连接处垂直位移坐标;K,K1,K2为悬架中对应弹簧刚度;c1,c2,c3为悬架中对应阻尼器阻尼系数;B为惯容器惯质系数;Kt为轮胎刚度;q为地面不平度。
2.2 随机路面时域信号生成
路面不平度是随机的,可抽象为满足一定条件的白噪声,经滤波器进行适当变换拟合输出具有指定谱特征的随机路面[8]。即:
(2)
式中:Gq(n0)为路面不平度系数;u为车速;ω(t)为均值等于零的高斯白噪声;n0为参考空间频率;n00为下截止空间频率。
2.3 时域动力学模型
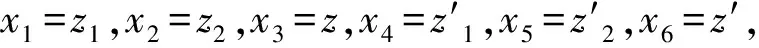
x′=Ax+Bxy=Cx+Du
(3)
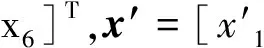
3 悬架参数优化
悬架性能评价指标有簧上质量加速度(ACC)、轮胎动载荷(DTL)及悬架动行程(SWS)等。其中ACC反映乘坐舒适性及车体振动环境,表达式为:
(4)
DTL即相对于静平衡位置时轮胎载荷变化,衡量轮胎抓地能力,反映高速时车辆行驶安全性,表达式为:
(5)
SWS即车轮相对车体垂直跳动动位移,反映车轮撞击限位器概率,表达式为:
SWS=x2-x1
(6)
悬架参数优化中,优化目标一般取ACC、DTL均方根值及SWS最大值。传统悬架系统中,ACC、SWS两目标变量相互矛盾,刚度、阻尼变化时,该两目标变量变化趋势相反。因此传统悬架优化一般仅选两变量进行优化,第三个按工程经验选取。ISD悬架可依靠惯容器以二阶微分形式配置系统传递函数极点,各目标变量间关系尚不明确,故按传统悬架处理方法,将SWS最大值作约束条件,以ACC、DTL均方根值为优化目标进行元件参数优化。
3.1 目标函数
将多目标优化转化为单目标优化方法简单、求解速度快。常见的转化方法包括主要目标法、线性加权法等。主要目标法仅一个优化目标函数,其余目标函数转化为约束条件;而线性加权法则将各目标函数通过加权求和方式转化为单目标函数,可有效权衡各目标函数,其数学模型为:
(7)
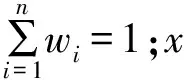
为抵消各目标函数单位、数量级影响,进行无量纲化后乘以反映各目标函数重要程度的加权系数。新型ISD悬架结构需与传统悬架对比,故针对某款成熟悬架进行归一化处理。侧重乘坐舒适性,取加权系数w1=0.6,w2=0.4[9],优化目标函数为:
(8)
式中:ACC*,DTL*(表1)分别为某款成熟悬架的ACC,DTL均方根值。minf(x)=1时,该新型悬架性能与传统被动悬架相近;minf(x)<1时,其性能优于传统被动悬架。以式(8)为目标函数,以悬架偏频及阻尼比为约束条件,对该款成熟悬架进行参数优化,得f(x)=0.989 725≈1,说明该款成熟悬架参数已接近最优解。
3.2 约束条件
为缩小参数的可行域,避免计算结果不符合工程实际,提出约束条件为:
(1) 正实约束:悬架参数仅为正实数时,才具有工程意义,即:
x≥0
(9)
(2) 偏频约束:该车悬架偏频ωn要求为(f1,f2),即:
(10)
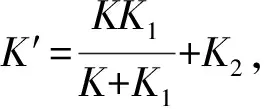
(11)
(3) 悬架动行程约束:悬架动行程最大值SWSmax(表1)不超过传统被动悬架,即:
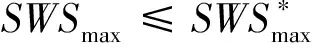
(12)
4 频率响应通用模型
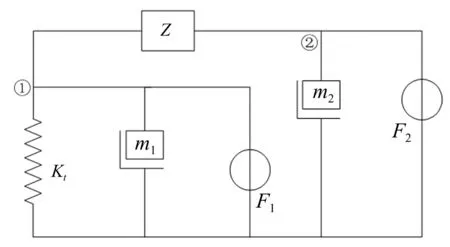
图3 ISD悬架1/4车体机械阻抗模型
机械阻抗指线性定常稳定系统的激励与其引起稳态响应的复数比。设新型ISD悬架结构的机械阻抗为Z,机械阻抗模型见图3[10]。类比电路中基尔霍夫定律,对节点①、②分析得系统力平衡方程为:
(13)
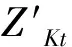
解方程组(13)得:
(14)
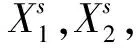
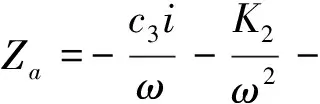
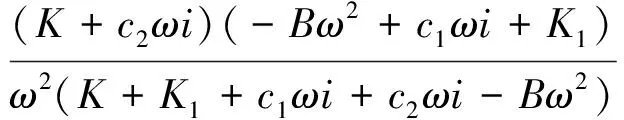
(15)
Zs=K2+c3ωi+
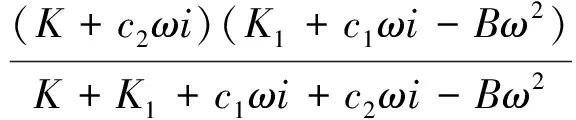
(16)
将式(15)、(16)代入式(14),可求得系统在固定频率范围内的频率响应及各悬架评价指标的频率响应,用于新型拓扑结构的对比分析。
5 典型结构ISD悬架特性仿真分析
某款车型参数见表1,采用上述21种悬架结构进行参数优化与幅频特性对比,获得12种性能优于传统悬架的结构。据悬架性能评价函数f(x)、新型悬架幅频特性及各元件参数,选表2的9种典型结构进行分析,结构见图4中S1~S9,幅频特性见图5~图13。

表1 车型参数
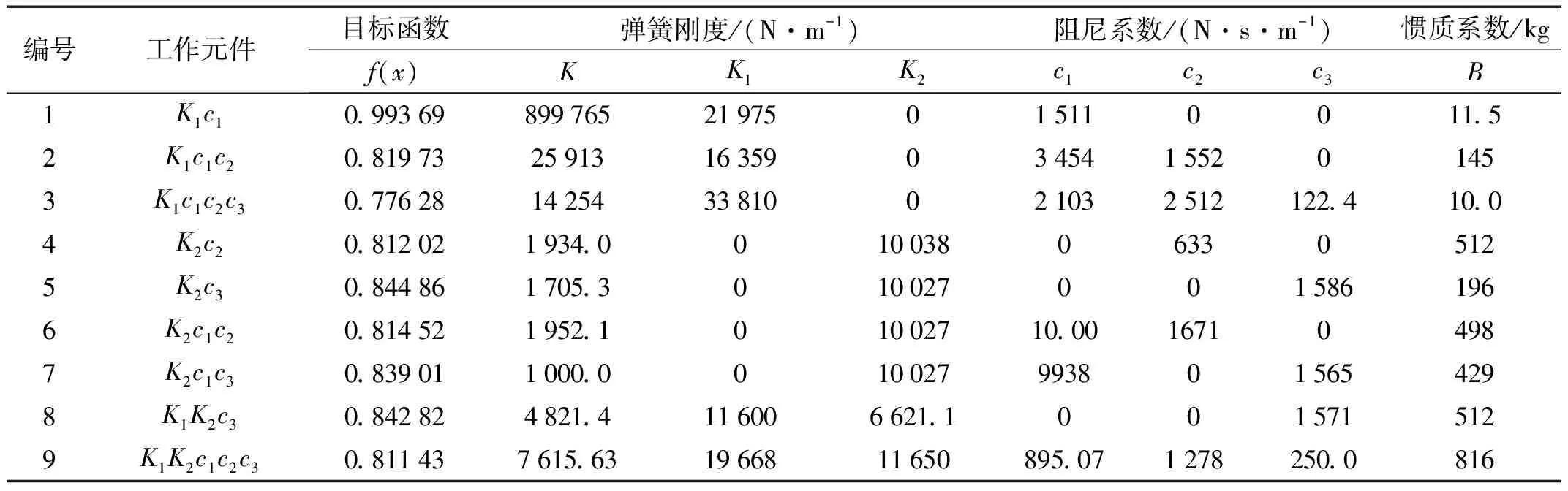
表2 典型结构ISD悬架参数
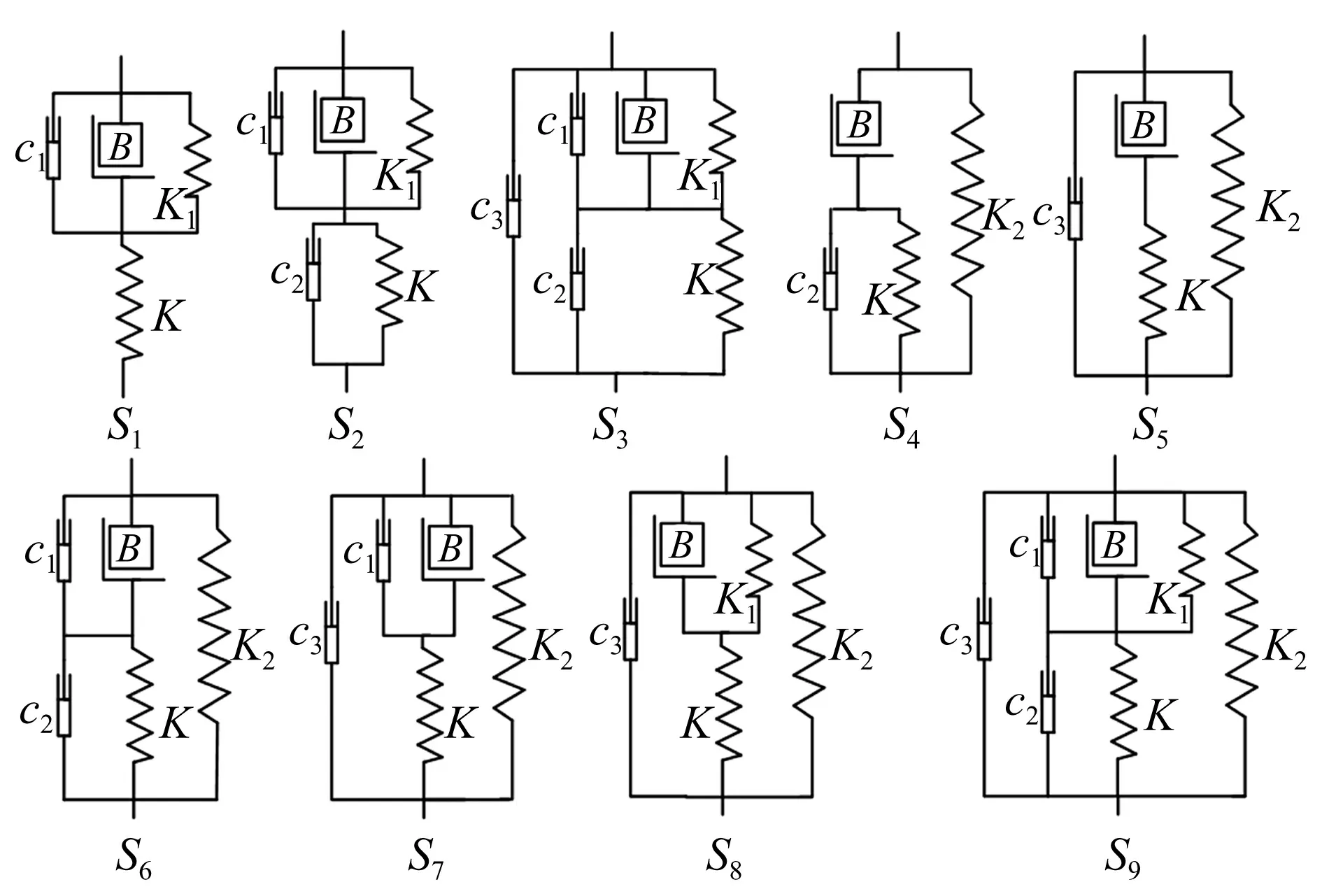
图4 ISD悬架结构
对S1,K远大于K1,B取值很小,相当于K短路,B开路,原结构等价于K1C1并联的传统悬架,f(x)≈1。由于增加一个自由度Z,在60 Hz处有明显共振尖峰,不适用于悬架系统。结构S2为两级串联型ISD悬架[5],由图6看出,该结构在低频段减振效果较好,车体加速度与悬架动行程均降低明显,打破了传统悬架中平顺性与操稳性矛盾,可用于悬架系统。结构S3中f(x)<1,性能优于传统悬架。由图7看出,车体加速度在低频段减振效果明显,高频段幅值略有增加,轮胎动载及悬架动行程的高频幅值变化较小,共振频率稍有前移,悬架整体性能有改善较大,但惯质系数较小,未充分发挥惯容器作用,该结构不适合作为ISD悬架。
结构S4即为基于ISD=元件理想匹配关系设计的新型结构[6],由图8看出,该结构在低频段减振效果较好,高频段幅值无明显增加,且结构简单,在ISD悬架中具有较大工程实现潜力。由图9看出,结构S5在低频段减振效果较好,高频段幅值无明显增加,性能优于传统被动悬架。虽其性能非最优,但结构简单,可视为在传统悬架基础上,并联1个惯容器与弹簧相串联的子结构,只需在传统悬架上稍作改进即可,亦有巨大工程应用价值。结构S6为在S4基础上增加阻尼器c1,由图10看出,该结构减振性能优于传统悬架,f(x)及各元件参数与S4相近,c1取值很小,相当于“开路”,原结构S6等价于S4。
由图11、图12看出,结构S7,S8在低频段的隔振效果优于传统悬架,且均与结构S5类似,适用于传统悬架基础上稍作改进,有较大工程应用价值。结构S9含1个惯容器、3个阻尼器、3个弹簧,在所有排列中最复杂,由图13看出,其性能优于传统悬架。因其结构复杂、可靠性差,不适合工程应用。
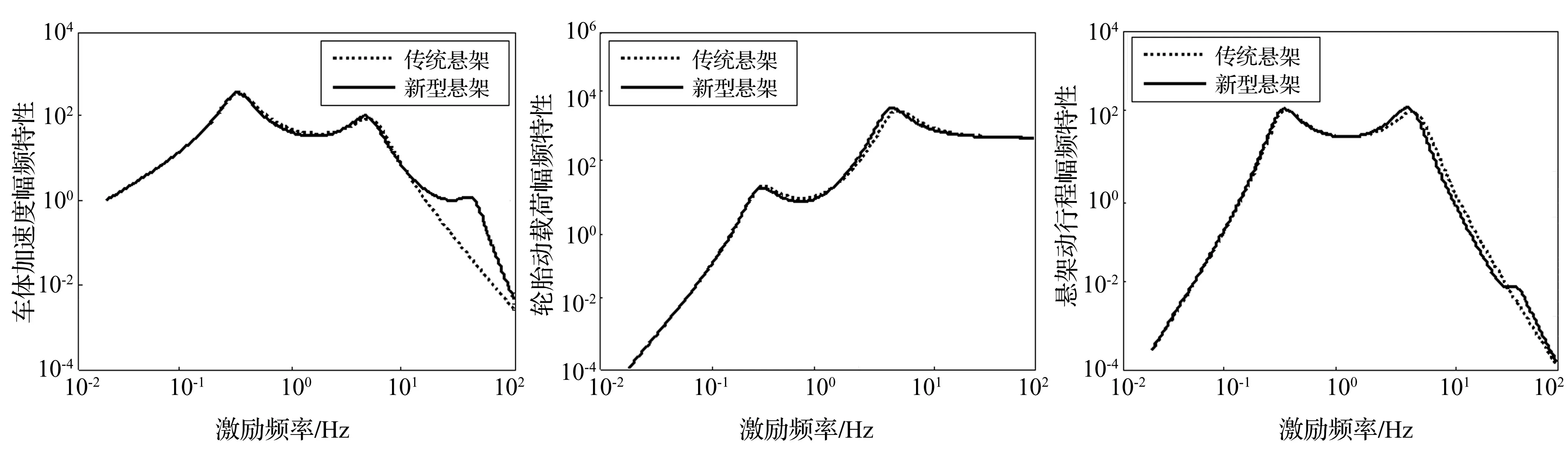
图5 S1性能指标对比图
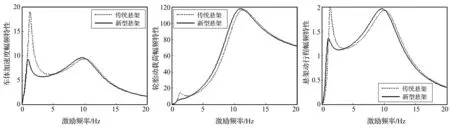
图6 S2性能指标对比图
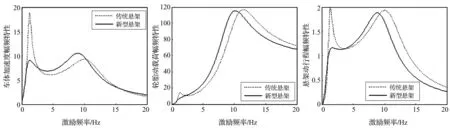
图7 S3性能指标对比图
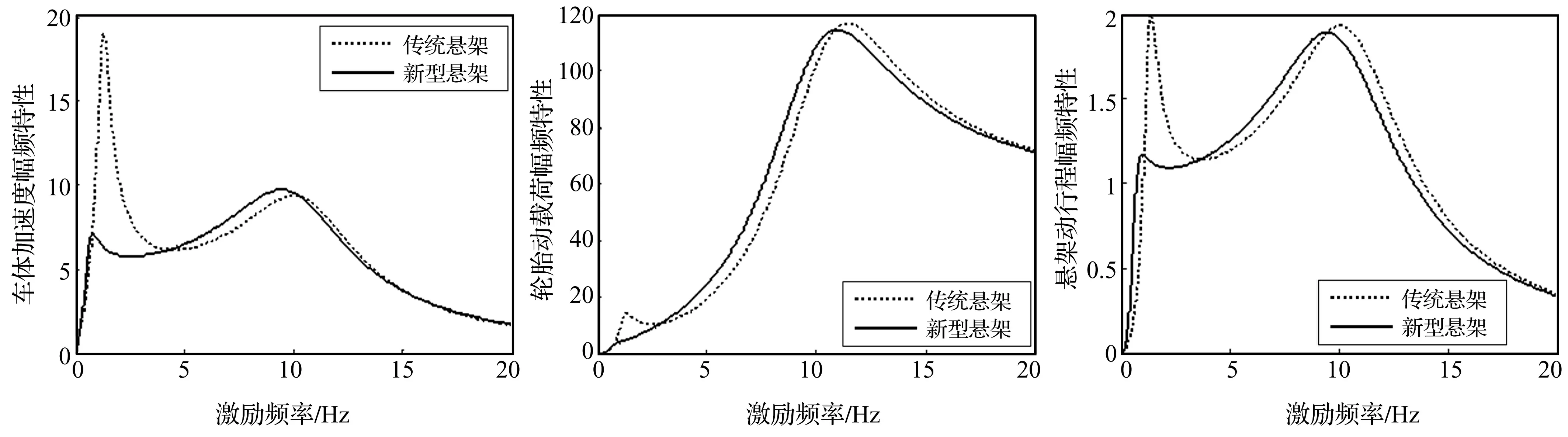
图8 S4性能指标对比图
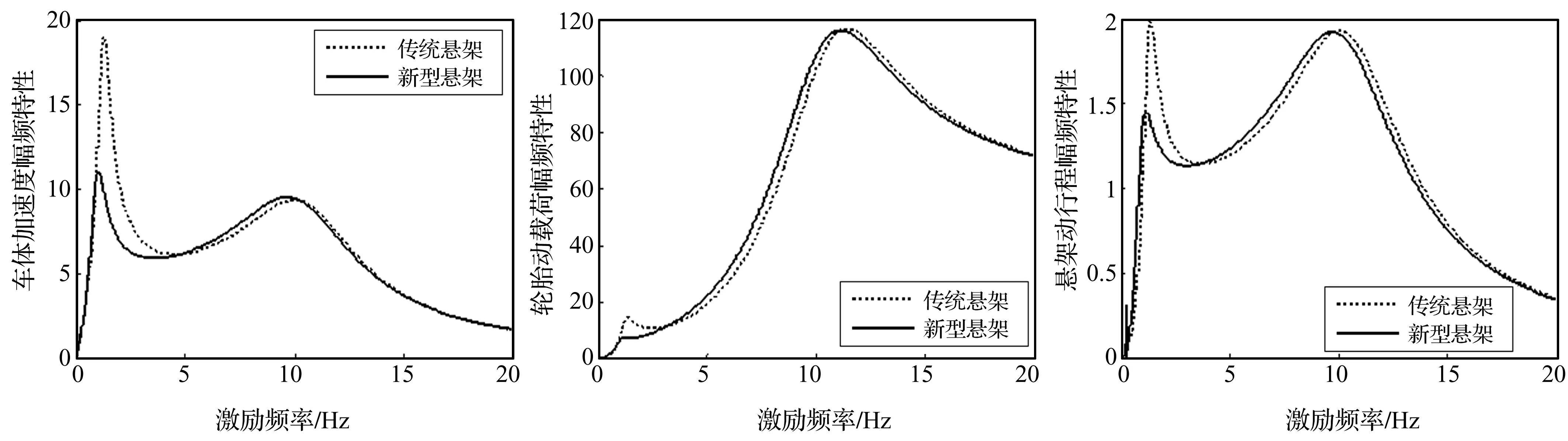
图9 S5性能指标对比图
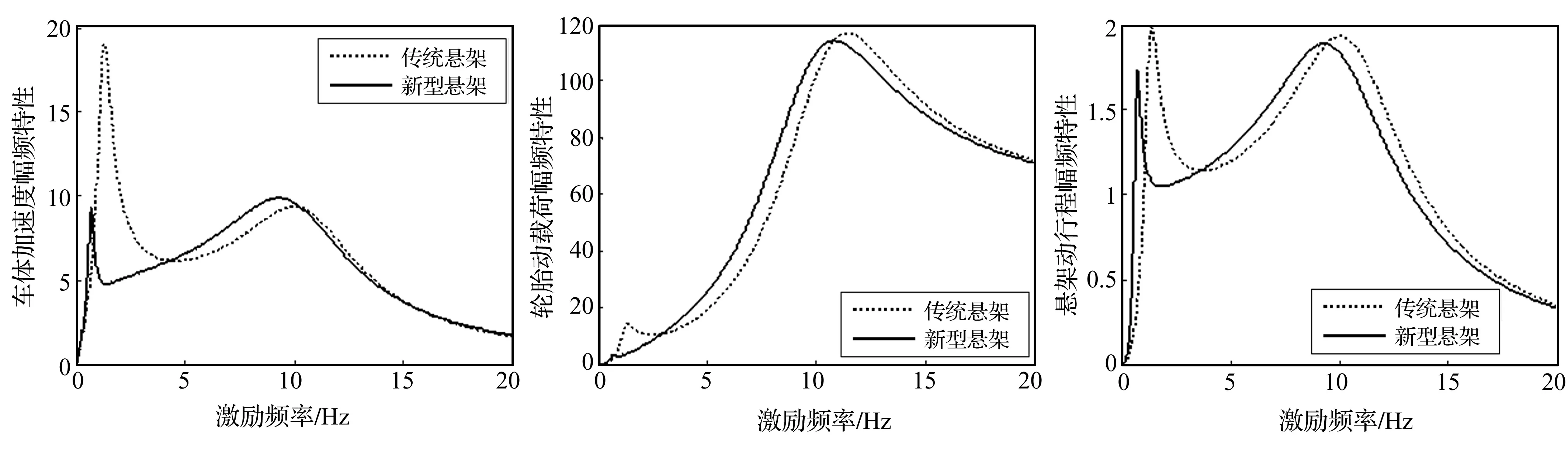
图10 S6性能指标对比图
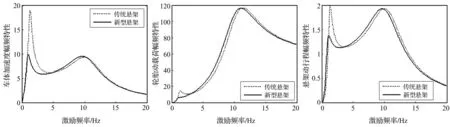
图11 S7性能指标对比图
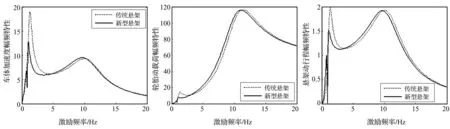
图12 S8性能指标对比图
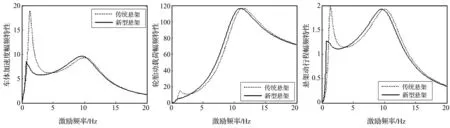
图13 S9性能指标对比图
6 结 论
(1) ISD悬架为新型悬架,通过对通用ISD悬架模型研究,找出性能优于传统弹簧-阻尼悬架的各种结构,对其中9种典型结构分析可知,有5种结构减振性能良好,且结构实现简单,工程应用潜力巨大。表明动力学建模与参数优化方法在ISD悬架设计中具有一般性、通用性。
(2) 由仿真知,ISD悬架在人体敏感的低频段隔振效果较好,高频段效果不明显。
参 考 文 献
[1]Smith M C, Wang F C. Performance benefits in passive vehicle suspensions employing inerters[J]. Vehicle System Dynamics, 2004, 42(4):235-257.
[2]Scheibe F, Smith M C. Analytical solutions for optimal ride comfort and tyre grip for passive vehicle suspensions[J]. Vehicle System Dynamics, 2009, 47(10):1229-1252.
[3]周玉坤. 电路[M].北京:电子工业出版社, 2012.
[4]罗胜钦, 刘 芳, 韩志刚. 网络综合原理[M].上海:同济大学出版社, 2009.
[5]陈 龙, 张孝良, 聂佳梅, 等. 基于半车模型的两级串联型ISD悬架性能分析[J]. 机械工程学报, 2012, 48(6):102-108.
CHEN Long, ZHANG Xiao-liang, NIE Jia-mei, et al. Performance analysis of two-stage series-connected inerter-spring-damper suspension based on half-car model[J]. Journal of Mechanical Engineering, 2012, 48(6):102-108.
[6]陈 龙, 杨晓峰, 汪若尘, 等. 基于而元件ISD结构隔振机理的车辆被动悬架设计与性能研究[J]. 振动与冲击, 2013, 32(6):90-95.
CHEN Long,YANG Xiao-feng,WANG Ruo-chen,et al.Design and performance study of vehicle passive suspension based on two-element inerter-spring-damper structrue vibration isolation mechanism[J].Journal of Vibration and Shock, 2013, 32(6): 90-95.
[7]余志生.汽车理论[M].北京:机械工业出版社, 2011.
[8]陈杰平, 陈无畏, 祝 辉,等. 基于Matlab/Simulink的随机路面建模与不平度仿真[J]. 农业机械学报, 2010, 41(3): 11-15.
CHEN Jie-ping, CHEN Wu-wei, ZHU Hui, et al. Modeling and simulation on stochastic road surface irregularity based on Matlab/Simulink[J]. Transactions of the Chinese Society for Agricultural Machinery, 2010, 41(3): 11-15.
[9]姜 鹏. 汽车悬架系统的仿真分析与参数优化设计[D]. 杭州:浙江大学, 2006.
[10]左鹤声.机械阻抗方法和应用[M].北京:机械工业出版社,1987.
