大型商用飞机撞击核电站屏蔽厂房荷载研究

刘晶波， 郑文凯

(清华大学 土木工程系，北京 100084)

至2011年底我国核电机组已建15台、在建26台，拟建21台[1]。在核电快速发展的同时，核电的安全性亦愈受重视。鉴于核电站的特殊性及核燃料泄漏后果的严重性，须重点考虑核电站安全性，尤其须确保核电站受火灾、地震、海啸、飞机撞击等极端情况的安全[2]。

“9·11”巨大灾难引起公众对大型商用飞机撞击重要构筑物的关注。随核电建设发展及大型商用飞机数量剧增，飞机撞击核电站问题亦引起重视。核电站设计中已开始考虑飞机撞击屏蔽厂房因素[3]。对此可直接用飞机有限元模型撞击核电站屏蔽厂房有限元模型方法进行分析计算，该方法除需建立核电站结构模型外，还需建立复杂的非线性飞机模型、考虑飞机与核电站动接触关系及两者的动力相互作用，计算较繁复。工程设计中希望能得到飞机撞击荷载时程曲线，利用该时程曲线直接加载考虑飞机的撞击作用，方便实用。但目前我国对飞机撞击荷载研究较少[4-5]。

本文利用ANSYS/LS-DYNA建立非线性飞机与核电站屏蔽厂房的有限元模型模拟撞击过程，考虑非线性、大变形、动接触等因素，通过发动机撞击钢筋混凝土板试验验证材料的本构模型及参数，对飞机网格分析确定其尺寸，对飞机以200 m/s速度撞击核电站进行分析，获得飞机撞击作用下核电站变形、破坏形式等规律。对假设的核电站采用线弹性、刚性本构模型，分析、对比核电站采用不同本构模型时撞击荷载时程，结果显示核电站刚度相对飞机较大，可采用撞击刚性体方法[6]确定飞机撞击合力的荷载时程曲线。但该方法无法给出荷载分布形式，仅建议将荷载均匀分布在机身作用面上。分析表明该分布方式结果与实际撞击结果相差较大。结论对确定核电站设计中飞机撞击荷载时程曲线与分布具有实用参考价值。

1 材料本构模型

大型商用飞机与核电站屏蔽厂房发生撞击时作用时间短、峰值大、应变率高，各种材料的力学性能与静载作用相比差距较大，故确定各种材料的本构模型较关键。大型商用飞机主要由铝合金与钢材组成。核电站屏蔽厂房主要材料为钢材及混凝土。本文对铝合金、钢材、混凝土材料的本构模型及参数取值进行分析研究。

1.1 钢材及铝合金材料本构

或飞机或核电站结构中的金属材料碰撞时材料的应变率效应十分明显，故选用考虑屈服、强化及应变率效应的Cowper-Symonds本构模型[7]，该模型为碰撞分析中常用的金属本构，屈服函数为：

(1)

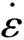
1.2 混凝土材料本构

由于核电站主要受力材料为混凝土，撞击荷载下需研究混凝土非线性本构关系及损伤，并考虑应变率效应。HJC[8]、Brittle_Damage[9]及Concrete_Damage[10]为动力分析的混凝土本构。本文选考虑钢筋作用、应变率效应、损伤效应、应变强化及软化作用的Concrete Damage本构模拟混凝土。该本构专为分析混凝土受爆炸及撞击作用，并定义三独立强度面：

(2)

其中：i分别为y,m,r代表初始屈服面、极限强度面、残余强度面；p=-I1/3为静水压力，可通过状态方程定义p与体积应变之关系；aji(j=0,1,2)为常数，由实验确定。

后继屈服面可利用参数η通过线性内插获得，参数η可反映屈服面强化、软化，且为与累计有效塑性应变相关函数，在0～1间变化。达到初始屈服面、未达极限强度面通过式(3)内插计算后继屈服面，此时η由0变到1；达到极限强度面后开始软化，采用式(4)内插后继屈服面，此时η由1变到0。

Δσ=ηΔσm+(1-η)Δσy

(3)

Δσ=ηΔσm+(1-η)Δσr

(4)

本模型参数较多，需较多实验确定，本文取实验参考值[7,11]。

1.3 材料模型及参数验证

1.3.1 验证试验

文献[12]用简化发动机分别以100 m/s、150 m/s、215 m/s速度对正方形钢筋混凝土板撞击试验。正方形板边长1.5 m，厚12 cm，板中纵筋配筋率0.4%，间距60 mm，直径6 mm，无箍筋。发动机见图1，总重3.5 kg。本文拟利用此试验对模型中混凝土、钢材本构及相关参数进行验证。

图1 试验用发动机模型(单位：mm)

试验测得混凝土圆柱体抗压强度23.5 MPa，密度2300 kg/m3；板中纵筋屈服强度447.2 MPa，弹性模量2.05×105MPa；发动机钢材屈服强度411.9 MPa，弹性模量2.14×105MPa。有限元模型中混凝土材料采用CONCRETE_DAMAGE本构，本构中应变率效应曲线用LS-DYNA经大量实验确定的推荐曲线[7]。钢筋、钢板均采用Cowper-Symonds本构，参数见表1。为模拟混凝土材料失效，用单元失效的EROSION算法，该算法可通过定义应力、应变等多种阀值控制单元失效，计算中需根据计算结果及试验结果对照确定相应阀值，由于混凝土应力变化大且本构曲线存在下降段，故选最大主应变控制单元失效，通过试算取最大失效主应变为0.17。

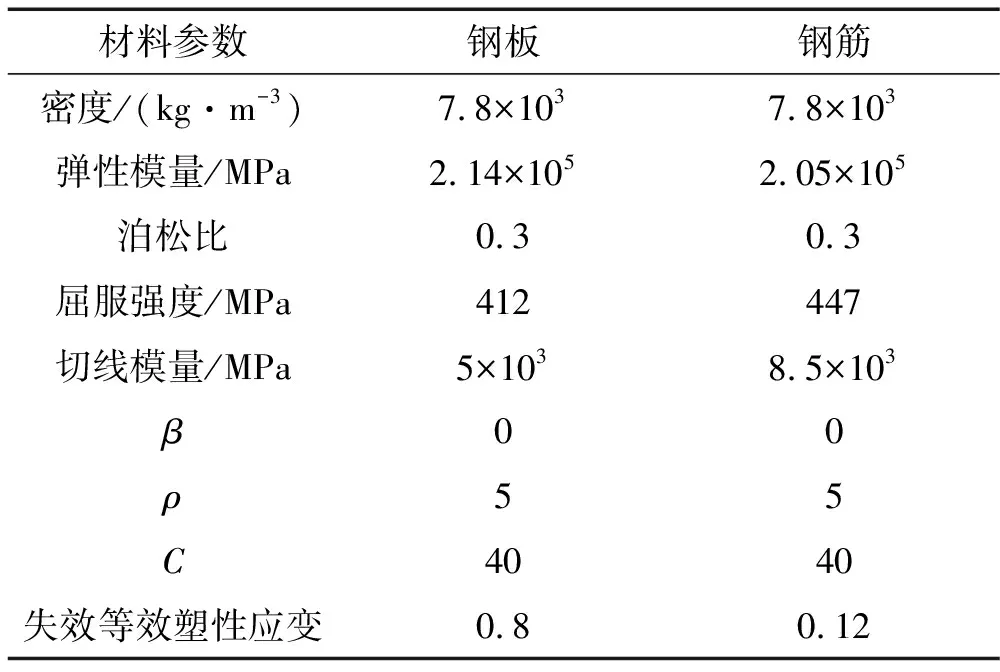
表1 钢板及钢筋材料参数

据试验建立有限元模型见图2。混凝土用单元尺寸30 mm的Solid164实体单元离散；钢筋用Link160杆单元离散，杆单元尺寸30 mm。钢筋、混凝土用共用节点建模。发动机钢板用Shell163壳单元离散，长度方向单元尺寸10 mm。模型单元总数285872个，钢筋混凝土板冲击背面四角点处，在200×200 mm范围内用固支约束。

用罚函数方法处理接触界面以模拟发动机对钢筋混凝土板的撞击作用，该方法根据接触时主、从界面相关节点的穿透情况引入与穿透深度、刚度成正比的界面接触力以保证接触界面不发生穿透。

在建立发动机与钢筋混凝土板有限元模型后，分别定义发动机与钢筋混凝土板中钢筋、混凝土的接触方式。发动机与钢筋接触方式用发动机为主界面的自动点面接触算法；发动机与混凝土接触方式用自动面面接触算法。罚函数方法中罚函数因子据实际接触中穿透情况调节，摩擦系数据实际接触表面情况确定。本文取罚函数因子1.0以防止穿透，摩擦等其它系数用默认值。

1.3.2 试验与数值模拟分析

图3(a)为数值模拟发动机以100 m/s速度撞击时混凝土板正面被撞击成坑，背面未破坏，与图3(b)试验照片形态大小一致。图4为发动机以150 m/s速度撞击时板正面、背面的破坏情况，正面混凝土破坏成坑，背面混凝土破坏脱落纵筋外露。图5为215 m/s撞击时穿透混凝土板，撞击处钢筋断裂，混凝土破坏，数值模拟发动机穿透后的剩余速度约52 m/s，与实验所测55 m/s较接近，破坏孔洞形态与实验一致。

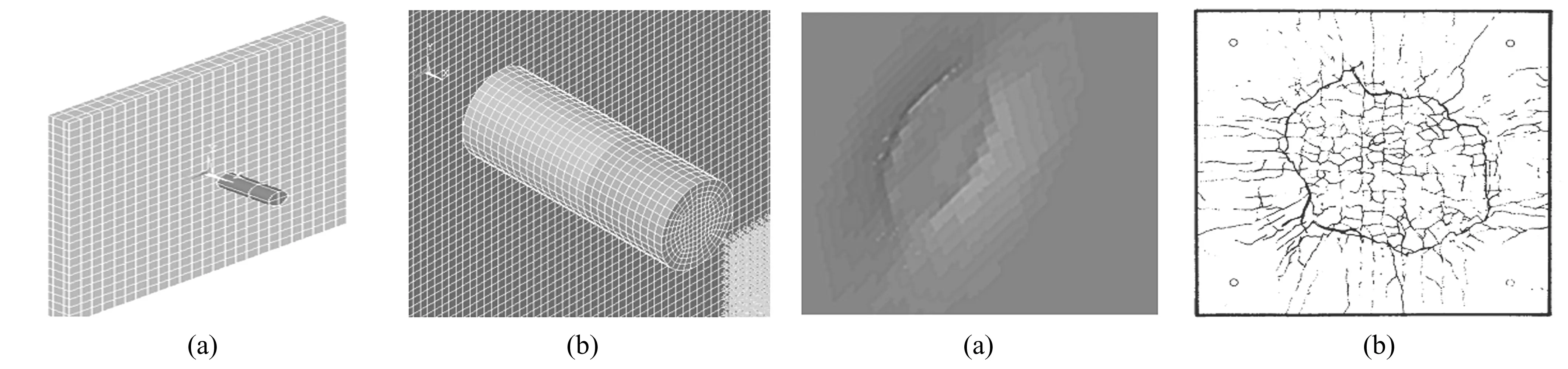
图2 发动机撞击钢筋混凝土板有限元模型

图4 150 m/s撞击时混凝土正面、背面破坏

撞击试验及数值模拟结果对比见表2。由表2看出，钢筋混凝土板的破坏类型、形态与实验一致，表明所用材料模型能较好模拟钢材、混凝土被冲击作用性质，且材料失效判断类型及参数取值合理。

表2 试验与数值模拟结果对比

2 核电站与飞机模型

2.1 核电站模型

以某型号核电站为原型并结合国际常用核电站结构尺寸建立核电站屏蔽厂房模型。筒体结构外半径22 m，高44 m，顶部近似半球形外半径22 m，屏蔽厂房由1 m厚混凝土双面包13 mm厚钢板组成。结构总高66 m，混凝土用Solid164实体单元划分，钢板用Shell163壳单元划分，考虑计算成本，单元边长25 cm，单元总数1018368，其中实体单元数678912。结合核电站屏蔽厂房工程实际，钢板与混凝土间认为连接可靠，用共用节点建模忽略两者间滑移，结构底部为固定边界。混凝土材料本构采用CONCRETE_DAMAGE本构，混凝土单轴抗压强度48 MPa，钢板用Cowper-Symonds本构，其它参数同前。

2.2 飞机模型

选飞机模型关键控制量为总质量、发动机质量及质量分布。常选撞击飞机重量、飞行量应能包络大多数的商用飞机[13]。由于难以获取精确的飞机构造等数据，本文以Boeing 767-200ER大型商用飞机尺寸、重量为参考[14]。飞机重80 t，发动机重约10 t，飞机总长48.5 m，添加地板及横隔板模拟内部结构。飞机全部采用壳单元离散；针对EROSION算法在单元失效时删除单元，飞机网格尺寸对撞击结果影响较大，故进行网格尺寸分析。图6为网格尺寸分别为1 m，0.25 m，0.125 m时飞机撞击刚体的撞击力合力，随网格尺寸减小计算趋于稳定。本文选飞机网格尺寸0.25 m，计算结果稳定且计算成本较小，飞机单元总数9148，飞机外形尺寸及有限元模型见图7。

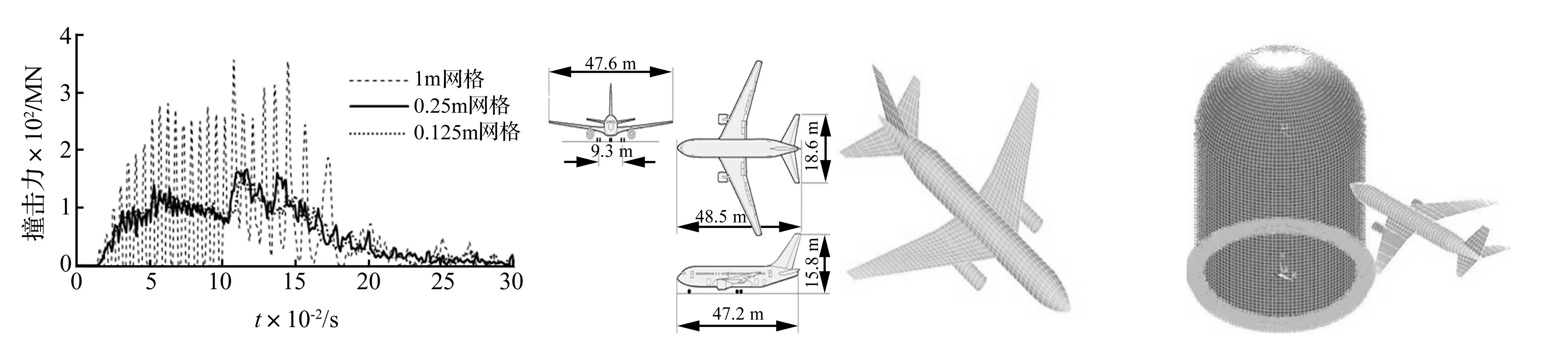
图6 网格尺寸对撞击力影响分析

3 飞机撞击核电站计算模拟

飞机撞击核电站屏蔽厂房分析中涉及到飞机的撞击位置、角度及速度。文献[15]指认为最不利撞击位置在筒体与半球交接处,而垂直撞击为屏蔽厂房整体分析中最不利作用方式，撞击速度取200 m/s。本文计算中飞机以200 m/s速度垂直撞击核电站筒体与半球交接处，见图8。

用上述有限元模型，撞击模型单元总数1027516，撞击中采用部件组定义接触为自动面面接触，其中罚函数作用系数为1.0以保证合理接触，材料模型及参数同上。本文仅考虑飞机撞击作用，未考虑飞机燃油燃烧及爆炸作用。撞击过程见图9，撞击结果显示飞机机身撞击部分已完全破坏，核电站模型撞击部位变形明显，机身及发动机巨大撞击导致被撞击区域混凝土破坏，发动机在飞机撞击中影响较大，其它区域反应较

小。图10为核电站结构距被撞击中心点上方3 m、5 m、7 m、9 m四个点及顶点的位移曲线，随距离撞击中心点越远撞击影响迅速减小，核电站顶点位移最大值仅15 mm。飞机机身未破坏部分速度见图11，飞机撞击力合力见图12，最大撞击力合力约170 MN。

图9 飞机撞击过程

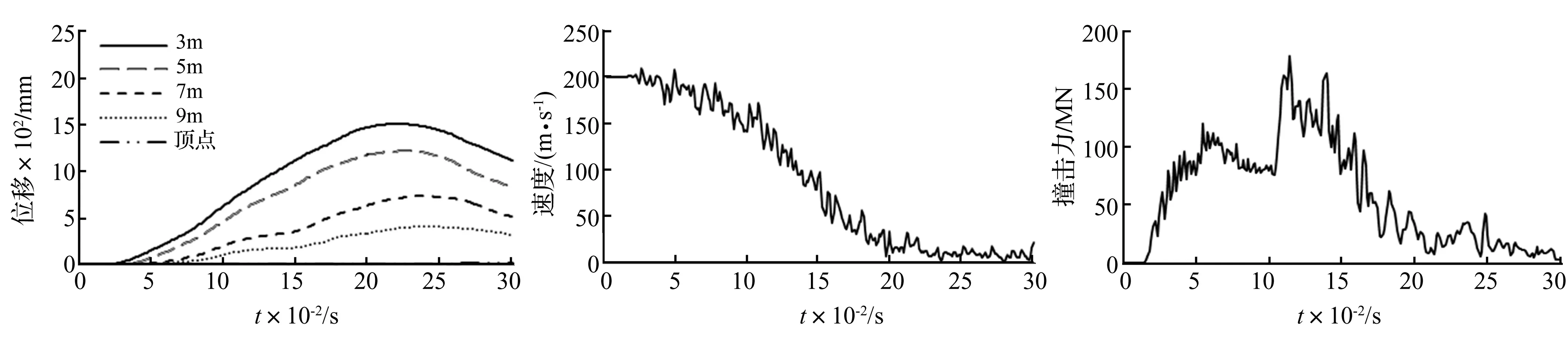
图10 结构位移曲线

4 撞击荷载分析与讨论

影响飞机撞击力的因素较多，如飞机质量大小、质量分布及材料性质、核电站屏蔽厂房外形尺寸及材料性质、飞机速度等。为进一步分析撞击荷载作用，用非线性飞机模型分别撞击刚性、线弹性核电站模型，获得撞击力曲线见图13。由图13看出，三种情况整体作用时间、形状及峰值相近，说明与飞机相比，核电站刚度较大，可设为刚性体或弹性体估算撞击合力。

由于核电站刚度相对飞机大，可采用撞击刚性体方法[6]分析飞机撞击合力的荷载时程曲线。该方法主要假设：飞机垂直撞击刚性体目标，飞机为质量沿长度方向分布的1维结构。据动量定理导出飞机撞击力计算式为：

F(t)=Pc(x)+μ(x)(dx/dx)2

(5)

其中：F(t)为飞机撞击力；x(t)为机头至t时刻压屈作用点距离；Pc(x)为飞机在x处压碎力；μ(x)为在x处单位长度飞机质量。用文献[6]方法求解飞机初速度200 m/s时的撞击荷载时程见图14。由图14看出，利用Riera方法所求撞击合力的荷载时程曲线与弹塑性数值模拟所得撞击合力除第2峰值列处相差较大外总体形状吻合较好，故可用该方法计算撞击合力的荷载时程曲线。但Riera方法无法给出撞击荷载分布形式，仅将荷载平均分布到飞机机身作用面积内，按均匀分布给核电站加载。模拟结果显示采用此加载方式计算时均布荷载边缘混凝土先遭破坏，破坏形态及原因与飞机撞击非线性核电站模拟结果差别较大。图15为均布加载时核电站结构上荷载作用中心点上方3 m、5 m、7 m、9 m四点与顶点位移曲线，与图10相比看出两者差异较大，撞击处位移及整体反应差别较大，说明不能简单将荷载均匀分布在机身作用面积上，需考虑不同部位各自荷载大小及分布。

图13 刚性体及线弹性体撞击力

5 结 论

(1)本文通过发动机撞击钢筋混凝土板试验确定CONCRETE_DAMAGE与Cowper-Symonds本构能较好模拟撞击作用下混凝土与金属材料性质，并确定接触算法及相关参数。通过用不同网格尺寸飞机撞击刚性体分析确定飞机模型合理网格尺寸。

(2)通过对大型商用飞机以200 m/s速度撞击钢板混凝土核电站屏蔽厂房的非线性动力时程分析结果显示，核电站被撞击部位变形明显，机身及发动机撞击发生破坏，其它区域变形较小，最大撞击合力约170 MN。

(3)将核电站用弹塑性模型时撞击合力荷载时程曲线与用刚性、线弹性体核电站模型撞击荷载对比，三种情况下曲线相近说明，与飞机相比，核电站刚度较大，可设核电站为刚性体或弹性体计算飞机撞击力合力，可用Riera方法推导出总撞击力荷载时程曲线。而该方法无法确定荷载分布形式，所用在机身作用面均匀加载方式所得结果与飞机撞击核电站非线性模型结果差别较大，故需对荷载分布形式进一步研究。

参 考 文 献

[1]赵小辉,邹树梁,刘 永.内陆核电发展形势分析[J]. 南华大学学报,2012,13(3):1-7.

ZHAO Xiao-hui,ZOU Shu-liang,LIU Yong. Analysis of inland nuclear power development situation[J]. Journal of University of South China, 2012, 13(3):1-7.

[2]王玉岚.核电站安全壳在外来事件作用下的安全防护性能研究进展[J]. 电网与清洁能源,2009,25(10):74-77.

WANG Yu-lan. Research progress of security performance of nuclear power plant suffering external events[J]. Power System and Clean Energy, 2009, 25(10):74-77.

[3]汤 搏.关于核电厂防大型商用飞机撞击的要求[J].核安全, 2010,3:1-16.

TANG Bo.Requirements for nuclear power plants against large commercial aircraft impact[J].Nuclear safety,2010,3:1-16.

[4]左家红.秦山核电厂安全壳在飞机撞击下的非线性分析[J].核科学与工程,1992,12(1):35-42.

ZUO Jia-hong. Nonlinear analysis of Qinshan nuclear power plant containment under impacting of the aircraft[J]. Nuclear Science and Engineering, 1992,12(1):35-42.

[5]王远功,余爱萍. 飞机撞击核反应堆安全壳荷载-时间曲线的确定[J]. 核科学与工程,1991,11(3):208-215.

WANG Yuan-gong,Yu Ai-ping. The determination of the load of the aircraft hitting the reactor containment[J]. Nuclear Science and Engineering, 1991, 11(3):208-215.

[6]Riera J D. On the stress analysis of structures subjected to aircraft impact forces[J].Nuclear Engineering and Design, 1968, 8(4):415-426.

[7]LS-DYNA Keyword User’s Manual,Version971,2007．

[8]Holmquist T J, Johnson G R. A computational constitutive model for concrete subjected to large strains, high strain rates, and high pressures[R]. Canada, Proceedings of the fourteenthInternational Symposium on ballistic, 1993.

[9]Govindjee S, Kay G J,Simo J C. Anisotropic modelling and numerical simulation of brittle damage in concrete[J]. International Journal for Numerical Methods in Engineering,1995,38(21):3611-3633.

[10]Malvar L J, Crawford J E, Wesevich J W,et al.A plasticity concrete materialmodel for DYNA3D[J].International Journal of Impact Engineering, 1997, 19( 9-10):847-873.

[11]Crawford J E, Magallanes J M, Lan S,et al. User’s manual and documentation for release III of the K&C concrete material model in LS-DYNA, TR-11-36-1[R].Technical Report, Karagozian & Case, Burbank, CA, 2011.

[12]Muto K, Tackihawa H, Sugano T, et al. Experimental studies on local damage of reinforced concretestructures by the impact of deformable missiles, part 1: outline of test program and small-scale tests SmiRT 10[R].Los Angeles, California: American Association For Structural Mechanics in Nuclear Reactors, 1989.

[13]EPRI.Deterring terrorism: aircraft crash impact analyses demonstrate nuclear power plant's structural strength [R]. America: Electric Power Research Institute, 2002.

[14]Boeing Commercial Airplanes[C]. http://www.boeing.com

[15]Prabhakar G, Ranjan R, Paul M K,et al.Analyses of aircraft impact on containment structure[C]. 5thAsia-Pacific Conference on Shock & Impact Loads on Structures. Changsha China, 2003:315-322.