基于POD的大涡模拟入流脉动合成方法研究

郑德乾， 顾 明， 张爱社

(1.河南工业大学 土木建筑学院，郑州 450001； 2.同济大学 土木工程防灾国家重点实验室，上海 200092； 3. 山东建筑大学 土木工程学院，济南 250101)

基于空间平均的大涡模拟(Large Eddy Simulation, LES)方法可同时获得结构表面的平均、脉动风荷载，且计算量适中，为应用前景广阔的数值模拟方法。进行大气边界层内高层建筑绕流问题的大涡模拟分析，应采取合适的入流边界条件生成方法，准确模拟紊流边界层风场，以保证结构风荷载预测精度[1]。

目前的LES入流脉动合成方法可分为两类：辅助域法[2-3]与直接合成法[4-9]。辅助域法为先在不含研究对象的计算域中进行LES计算，保存计算域某位置处脉动风速时程作为大涡模拟的入流边界条件。虽辅助域法生成的入流脉动物理意义清晰，但合成过程较耗时。直接合成法则直接在入流面上直接合成具有指定统计特性及谱特性的脉动风速时程。一般通过在入流面的平均风剖面上叠加由蒙特卡罗法[4-5]或数字滤波法[6]生成的脉动风速时程序列合成LES入流脉动。与辅助域法相比，直接合成法更高效、便捷。本文采用直接合成法获得LES入流脉动。

在LES计算中，为捕捉流场中尽量多的小尺度涡，致网格数目庞大，需采用并行计算技术提高计算效率。与串行计算不同，在流场并行计算中，不同的计算域网格分块由不同计算节点负责，限制了多数LES入流脉动直接合成法在并行计算中的应用。解决办法为在入流面各网格点独立合成脉动风速时程[7-9]，但该类方法脉动风速合成需通过对三维能量谱离散实现，而风工程中脉动风速谱多为频谱形式。故需发展既可通过离散频谱形式风速谱合成脉动风速时程，又适用流体并行计算的LES入流脉动直接合成方法。

本文以Karman谱为目标谱，采用特征正交分解(Proper Orthogonal Decomposition, POD)型谱表示法[10]合成脉动风速时程。针对流体并行计算特点，发展适用于流体并行计算的LES入流脉动合成方法，以提高LES方法进行紊流风场内结构风荷载的预测精度。基于Fluent软件平台，分别通过空计算域紊流边界层风场及宽高比1∶6的单体方形截面高层建筑非定常绕流的LES计算结果与刚性模型测压试验[11]结果比较，验证本文方法的有效性。

1 风洞试验

某高层建筑宽高比1∶6，见图1(a)，B=D=0.1 m，H=0.6 m，其刚性模型同步测压风洞试验在同济大学土木工程防灾国家重点实验室风洞试验室TJ-2大气边界层风洞中进行[11]，模型缩尺比1∶500。据该高层建筑所处地面粗糙度类别，按1/500缩尺比模拟B类风场，试验所测平均风剖面与湍流度剖面见图1(b)、(c)。试验时将模型置于转盘中心，通过转盘模拟不同风向角。限于篇幅，本文主要对图1(a)中0°风向角(来流垂直吹向结构)进行大涡模拟计算。风洞试验中结构表面共布置200测点，此处仅给出用于本文数值模拟与风洞试验比较的模型表面主要测点(图1(a))。详细风洞试验结果见文献[11]。

2 LES入流脉动合成

LES计算中入流面网格数量庞大，本文基于POD型谱表示法[10]合成入流面主要网格点的脉动风速时程，采用有限元形函数进行空间插值得出入流面所有网格点的脉动风速时程。据流体并行计算各节点调用关系及数据存储特点，编程实现流体并行计算时已合成脉动风速时程序列的读入、赋值。并给出LES入流脉动合成方法的基本原理与实施步骤。

图1 风洞试验测点布置及试验风剖面

2.1 POD型谱表示法

POD特征正交分解为分析复杂随机场统计特征的有效工具，该方法通过建立新坐标空间，采用时空分离技术简化随机现象描述。文献[10]将POD法引入桥梁随机风场模拟中发展了POD型谱表示法。该方法物理意义明确，可通过模态截断提高计算效率。

对一维N变量零均值的平稳随机过程，其功率谱密度矩阵可表示为：

(1)

其中：ω为脉动风速圆频率；Sij(ω)(i,j=1,2,3,…,N)，i=j时Sij(ω)为脉动风速自功率谱密度函数；i≠j时Sij(ω)为脉动风速互功率谱密度函数。

为模拟获得具有指定谱密度函数形式的脉动风速时程，需对式(1)谱密度矩阵[S(ω)]进行分解。采用原型谱表示法(如谐波合成法)时，对谱密度矩阵[S(ω)]一般采用Cholesky分解，而POD型谱法则采用POD方法分解[10]，即：

(2)

式中：[φ1(ω)], [φ2(ω)],…, [φN(ω)]与η1(ω),η2(ω),…,ηN(ω)分别为谱密度矩阵[S(ω)]的N阶特征向量、特征值，特征向量按特征值降序排列，满足正交化条件[10]：

(3)

式中：δ为Dirac-δ函数。谱矩阵特征值代表对应振型包含振动能量大小，谱振型则由频域描述随机过程包含能量的空间分布形式，具有特定物理意义。若前NS阶谱振型所含能量足够大，则可引入模态截断技术进行模型缩减[10]：

(4)

采用POD型谱表示法时，某点脉动风速时程表达式[10]为：

(5)

式中：θkl为在[0,2π]间均匀分布的独立随机相位角；Δω为频率步长；ωl= (l-1)Δω为频率采样点序列。

误差分析[10]表明，POD型谱表示法总体相对随机误差与根方差相对随机误差小于原型谱表示法。本文用式(5)的POD型谱表示法合成具有指定频谱特性的脉动风速时程。

2.2 LES入流脉动合成参数选择

2.2.1 平均风剖面

用对数律表达式[12]描述平均风速沿高度变化：

(6)

式中：κ=0.42为冯·卡曼常数；u*为摩擦速度；z0为粗糙长度，由图1(b)试验平均风剖面拟合获得，见表1。图1(b)比较结果显示平均风剖面拟合值与试验值吻合较好。

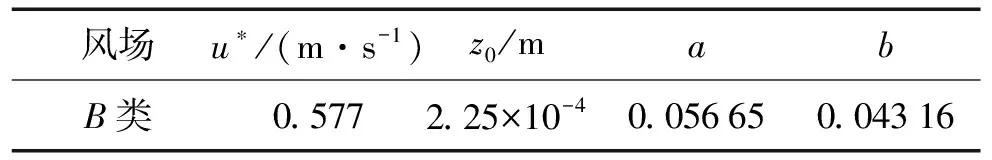
表1 B类1∶500缩尺比风场参数拟合值

2.2.2 湍流度剖面

数值计算时，湍流模型中湍流黏度系数与紊流强度成正比，近地面处湍流强度过大易致湍流黏度系数过高而影响数值计算收敛，因此风洞试验风场的湍流度剖面采用分段函数进行拟合：

(7)

式中：a，b为常数，由图1(c)试验湍流度剖面拟合获得(表1)。湍流度剖面拟合值与试验值比较见图1(c)，由图1看出，二者一致性较好。

2.2.3 纵向湍流积分尺度

本文缺少相应纵向湍流积分尺度随高度变化的试验值，而基于不同湍流积分尺度建议公式值有所不同。纵向湍流积分尺度采用日本AIJ规范[13]建议表达式。为便于同风洞试验结果比较，本文模拟与风洞试验相对缩尺比1∶500风场，修正后纵向湍流积分尺度计算式为：

(8)

式中：λL为模型几何缩尺比，λL=500。

2.2.4 脉动风速谱

Karman谱能反映脉动风速沿高度变化，本文以其为目标风速谱，Karman谱表达式变化形式为：

(9)

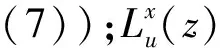
2.2.5 脉动风速相干函数

纵向脉动风速竖向、横向相干函数表达式为[14]：

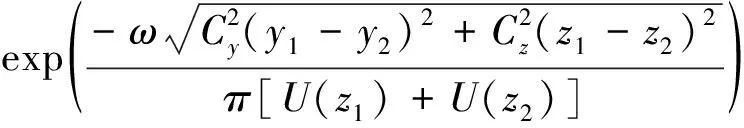
(10)

式中：r为空间两点距离；y1，y2，z1，z2分别为空间两点横、竖坐标；U(z1)，U(z2)分别为高度z1，z2处平均风速；Cy，Cz分别为横、竖向相干指数衰减系数，与平均风速、离地高度、地面粗糙度有关，取Cy=16，Cz=10。

2.3 入流面网格点脉动风速合成步骤

为尽量捕捉到较小涡运动，LES计算中需较密网格布置，使入流面网格点数增大，若同时生成入流面所有网格点脉动风速时程耗时耗力。故采取入流面网格点分组循环[4]，或分若干块并假设各分块内网格点风速完全相关[5]等措施生成入流面脉动风速。前者实施较麻烦，后者会造成所得入流面上速度场不连续。本文采用有限元形函数，空间插值出入流面所有网格点的LES入流脉动，尽量保证速度场的连续性。考虑入流面网格多为规则矩形，故采用矩形等参单元进行形函数计算、插值，实施步骤为：

(1)在LES入流面上生成一定数目的点坐标，且应含入流面边界上4个顶点，并在近地面及模型高度附近区域较密分布，见图2(a)中“●”；

(2)据点空间位置关系，在步骤(1)生成点分别组成的矩形有限单元内，选所含相应的LES入流面网格点(图2(b))，分别计算网格点在所属矩形单元的形函数；

(3)用式(5)POD型谱表示法同时生成步骤(1)点的脉动风速时程，即获得步骤(2)中各矩形单元4顶点的脉动风速时程；

(4)据步骤(2)所得入流面网格点在所属单元的形函数及步骤(3)生成矩形单元4顶点的脉动风速时程，依次插值出最终LES入流面所有网格点的脉动风速时程。

图2 LES入流面网格点脉动风速空间插值示意图

除空间插值问题外，LES计算中较小时间步长亦会带来脉动风速时程时间插值问题。本文通过用POD型谱表示法直接生成与LES计算相同时间步长的脉动风速时间序列避免该问题。

2.4 并行计算中入流面网格点脉动风速时程读入

与串行计算相比，流体采用并行计算技术时，需对计算域网格进行分区，不同网格分区由不同计算节点负责，并通过不同区间的重叠网格实现计算节点间数据传输，见图3(a)。并行计算存在主进程及若干计算节点等多个进程，见图3(b)，其中主进程不含任何网格信息，主要负责外部数据存储文件的开、关及进行命令解释与传递；0#计算节点负责命令分发及数据收集[15]。因此，LES并行计算时，需针对并行计算特点采用相应措施确保合成的脉动风速时程准确读入与赋值。本文先由主进程读取外部存储的脉动风速时程数据文件，传递给0#计算节点；0#计算节点将脉动风速时程数据分发给所有计算节点；各计算节点将各自脉动风速数据分别赋值给负责的入流面分区网格点。通过合成的脉动风速时程数据分时刻存储及LES计算中分时刻读入网格点风速值方法提高LES计算效率；通过将LES非定常迭代时间步引入风速数据存储矩阵办法解决LES计算因故中断退出后继续计算时入流面网格点风速值的正确读入问题。以上处理方法，本文用Fluent UDF编程实现。

图3 Fluent并行计算网格分区及命令传递示意图[15]

3 单体方形截面高层建筑大涡模拟

基于Fluent软件平台，采用与风洞试验[11]相同比例缩尺比，进行B类1:500缩尺风场方形截面高层建筑的LES非定常绕流计算。计算域94D×28D× 36D，见图4(a)。采用非均匀结构化网格对计算域进行离散，近壁面处网格加密，见图4(b)、(c)，最小网格尺度1/2000D，对应壁面y+值小于5.0。采用网格总数分别为151万(G1)、90万(G2)两种划分方法。采用速度入口边界条件，为考察本文方法的有效性及精度，LES入流脉动合成分别采用本文方法及Fluent内置改进合成法[9]。计算域其它位置边界条件设置见图4(a)。

表2为本文LES计算工况，压力速度耦合均采用SIMPLEC算法，空间离散采用具有二阶精度的bounded central differencing格式；时间离散采用二阶全隐格式，时间步长0.0005 s；亚格子模型采用Dynamic Smagorinsky-Lilly模型[16]。

表2 单体方形截面高层建筑LES计算工况

图4 LES计算域、边界条件设置及离散网格示意图

4 结果与讨论

图5为本文考虑工况下，数值模拟所得距离模型前方5D处的模拟风剖面、速度监测点脉动风速谱，与试验[11]风剖面及Karman谱的比较。由图5看出，①所有工况下，数值模拟所得平均风剖面与风洞试验结果基本一致；②数值模拟所得紊流度剖面在远离地面处与试验结果吻合相对较好，而在近地面处均有所衰减，相同网格密度下与结果[9](G1_LES1工况)相比，采用本文方法合成LES入流脉动(G1_LES2工况)，数值模拟所得紊流度剖面近地面衰减有所改善；③数值模拟所得脉动风速谱在低频处均稍高于Karman谱而高频处产生衰减，可能因LES计算网格分辨率不足以捕捉到更小尺度的涡(高频涡)所致。采用较密网格布置及本文方法合成LES入流脉动(G1_LES2工况)时，脉动风速谱在高频处的衰减有所减弱，与Karman谱一致性更好。本文LES数值模拟计算所得脉动风速谱基本能捕捉到无量纲频率在0.2～1.0范围内工程中所需高频脉动风速谱段即惯性子区段。

图5 LES模拟风场与试验结果的比较

图6为结构表面2/3H高度处测点平均和根方差风压系数的LES计算结果与风洞试验[11]结果比较，图中CP,mean，CP,rms分别为测点平均与根方差风压系数，此处及下文中结构表面风压系数均用模型高度处来流风速无量纲化。由图6看出，①所有工况下，LES计算所得平均风压系数均与风洞试验结果基本吻合，但在结构背风面LES计算结果均较高估计风吸力，此因结构背风面处于流动分离后的尾流区，流动相对复杂，气流分离会使风吸力较大；②根方差风压系数虽与风洞试验结果有偏差，但趋势基本一致，相同网格密度下，与结果[9](G1_LES1工况)相比，用本文方法合成LES入流脉动(G1_LES2工况)结果稍高地估计结构表面风压脉动；采用较稀疏网格布置(G2_LES2工况)过高估计侧面风压脉动值，此因较稀疏网格布置不足以准确捕捉结构侧面的流动分离现象。

图6 LES模拟所得高层建筑表面2/3H高度处风压系数统计值与试验结果比较

图7 LES模拟所得高层建筑表面2/3H高度处风压系数自谱与试验结果比较

图8 LES模拟所得高层建筑表面2/3H高度处风压系数水平相干性与试验结果比较

图7、图8分别为数值模拟所得结构表面2/3H高度测点风压系数自谱和水平相干性与风洞试验[11]结果比较。由图7看出，①在结构迎风面，LES计算所得风压系数自谱在高频处衰减较快，此因结构迎风面风压直接受来流紊流影响，模拟脉动风速谱均在高频处衰减所致；②在结构侧、背风面，LES计算所得风压系数自谱与风洞试验结果差别较小，结构侧面LES计算及风洞试验所得横风向旋涡脱落无量纲频率均为0.1，LES计算结果在高频处所含频率成分较少，此因网格过滤效应作用所致。由图8看出，LES计算所得结构测点风压系数的水平相干性随频率变化较平缓光滑，在低频处与风洞试验结果吻合较好，而在高频处与风洞试验结果均值线较接近，LES结果基本反映出测点风压系数水平相干性随频率变化规律。

5 结 论

针对流体并行计算特点，基于POD型谱表示法，发展适于流体并行计算的LES入流脉动合成方法。基于Fluent软件平台，进行宽高比1∶6的单体方形截面高层建筑非定常绕流LES计算，通过数值模拟所得风场特性、风压系数统计值及谱特性，与风洞试验及文献数值模拟结果比较，验证本文方法的有效性，结论如下：

(1)对紊流风场，本文方法可较好模拟平均风剖面及紊流度剖面，一定程度上能抑制近地面处紊流度及模拟脉动风速谱高频处的衰减现象。

(2)对结构表面风压预测，采用较密网格布置及本文方法合成LES入流脉动，不仅能较好进行结构表面风压分布预测，且能较准确给出风压系数自谱与水平相干性结果。

参 考 文 献

[1]Tamura T. Towards practical use of LES in wind engineering [J].Journal of Wind Engineering and Industrial Aerodynamics, 2008, 96(10-11): 1451-1471.

[2]Lund T S, Wu X, Squires K D. Generation of turbulent inflow data for spatially-developing boundary layer simulations[J].Journal of Computational Physics,1998, 140(2): 233-258.

[3]朱伟亮, 杨庆山. 湍流边界层中低矮建筑绕流大涡模拟[J]. 建筑结构学报, 2010, 31(10): 41-47.

ZHU Wei-liang, YANG Qing-shan. Large eddy simulation of flow around a low-rise building immersed in turbulent boundary layer[J]. Journal of Building Structures,2010, 31(10): 41-47.

[4]Kondo K, Murakami S, Mochida A. Generation of velocity fluctuations for inflow boundary condition of LES[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1997, 67-68: 51-64.

[5]李清雅, 叶继红. 三维空间曲面结构风荷载的数值模拟[J]. 振动与冲击, 2009, 28(4): 121-126.

LI Qing-ya, YE Ji-hong. Numerical simulation of wind pressure on spatial structures[J]. Journal of Vabraion and Shock, 2009, 28(4): 121-126.

[6]Klein M, Sadiki A, Janicka J. A digital filter based generation of inflow data for spatially developing direct numerical or large eddy simulations[J].Journal of Computational Physics, 2003, 186(2): 652-665.

[7]Smirnov A, Shi S, Celik I. Random flow generation technique for large eddy simulations and particle-dynamics modeling [J]. Journal of Fluids Engineering, 2001, 123(2): 359-371.

[8]Huang S H, Li Q S, Wu J R. A general inflow turbulence generator for large eddy simulation [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2010, 98(10-11): 600-617.

[9]ZHENG De-qian, ZHANG Ai-she, GU Ming. Improvement of inflow boundary condition in Large Eddy Simulation of flow around a tall building [J]. Engineering Applications of Computational Fluid Mechanics, 2012, 6(4): 633-647.

[10]胡 亮. 基于特征正交分解的桥梁风场随机模拟[D]. 武汉：华中科技大学, 2007.

[11]唐 意.高层建筑弯扭耦合风致振动及静力等效风荷载研究 [D].上海：同济大学, 2006.

[12]Richards P J, Hoxey R P Appropriate boundary conditions for computational wind engineering models using the k-ε turbulence model[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1993, 46-47: 145-153.

[13]Architectural Institute of Japan (AIJ), Recommendations for loads on buildings [S]. Japan, 2004.

[14]Davenport A G. The dependence of wind load upon meteorological parameters[C]. Proceedings of the international research seminar on wind effects on building and structures, University of Toronto Press, Toronto, 1968: 19-82.

[15]Fluent 6 documentation [M]. Fluent Inc, 2005.

[16]Lilly D K. A proposed modification of the Germano subgrid-scale closure model [J]. Physics of Fluids,1992, 4: 633-635.