热环境中功能梯度圆柱壳的内共振非线性模态

杜长城， 李映辉， 金学松

(1. 西南交通大学 力学与工程学院，成都 610031；2. 西南交通大学 牵引动力国家重点实验室，成都 610031)

功能梯度材料(FGMs)因其优良特性，在航空航天等诸多工程领域应用前景非常广阔，受到高度关注[1]。近年来，国内外对FGM薄壁结构振动及FGM结构非线性振动特性研究获得较多成果[2-8]。Alijani等[9]采用多尺度法分析具有矩形底面的双向曲线型FGM浅壳非线性主共振及次谐共振响应，获得分岔图及Poincaré映射，并给出系统的混沌域、揭示系统的复杂非线性动力学特性。张志强等[10]分析热环境中FGM圆板非线性振动时可能出现的周期、拟周期及混沌响应。杜长城[11]系统研究无限长FGM圆柱壳在非线性振动中的模态相互作用及主共振特性，分析材料性质、温度等对系统特性影响，讨论系统复杂分岔行为。

在研究非线性振动系统时提出的非线性模态(Nonlinear Normal Modes, NNM)概念，众多研究已表明其在讨论非线性系统定性性质中的必要性[12-14]。本文在文献[11]基础上，引入非线性模态概念，研究具有1∶2内共振的无限长FGM圆柱壳在热环境中非线性自由振动，讨论材料梯度指数与温度等因素对系统非线性模态频响特性影响。

1 基本方程

考虑中曲面半径R、厚度h的无限长FGM薄壁圆柱壳，在中曲面建立参考柱坐标系(x,θ,z)，其中x为柱壳轴向，θ为柱壳周向，z为柱壳径向(向外为正)；并设w为柱壳横向位移(z向位移)。设组成此功能梯度圆柱壳的组分材料分别为金属、陶瓷，且柱壳内表面为陶瓷外表面为金属。计入材料特性的温度相关性，设组分材料性能参数Pj(P表示E、ν、ρ等，j表示金属或陶瓷)随温度变化关系式为[2]：

(1)

其中：T=T0+ ΔT为温度，T0= 300 K为参考温度，ΔT为温度变化，本文中考虑均匀的稳态温变过程。材料参数温度特性见表1。采用幂律分布规律描述FGM等效材料参数[2,11]：

(2)

式中：Pm，Pc分别为金属、陶瓷材料参数；N∈ [0,∞)为梯度指数，反映金属体积分数沿厚度变化规律。

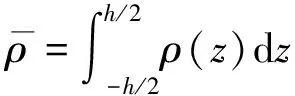
(3)

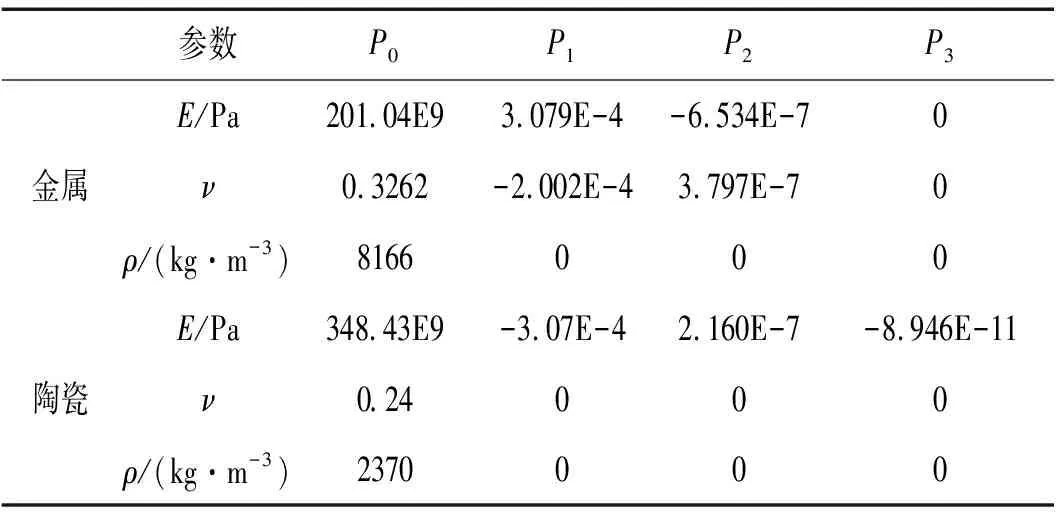
表1 金属与陶瓷温度相关参数(P-1 = 0)

选择两典型模态，设无限长FGM柱壳位移为：

w(x,θ,t)=

(4)

式中：等号右边第一项为非轴对称模态(n≠ 0),第二项为轴对称模态；L为模态轴向波长。研究表明此两模态的相互作用在柱壳稳定性中非常重要[15]。因无外部约束，温度改变时无限长柱壳始终处于自由应力状态，温度主要改变材料特性进而影响柱壳响应。故文献[11]的动能、势能表达式仍成立。无限长FGM柱壳动能为[11]：

(5)

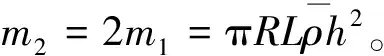
系统势能为[11]：

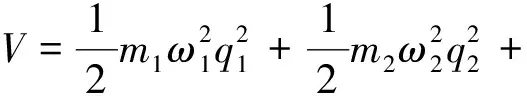
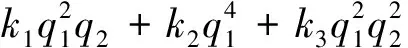
(6)

定义s=πR/L为轴向波长参数，据文献[11]有：

(7)

(8)

式中：s1为纯几何判据；s2不仅与柱壳几何参数相关，亦依赖于FGM柱壳材料性质。因此梯度指数N与温度会改变无限长FGM圆柱壳的理想内共振条件s2。

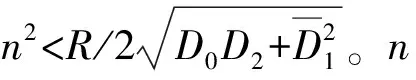
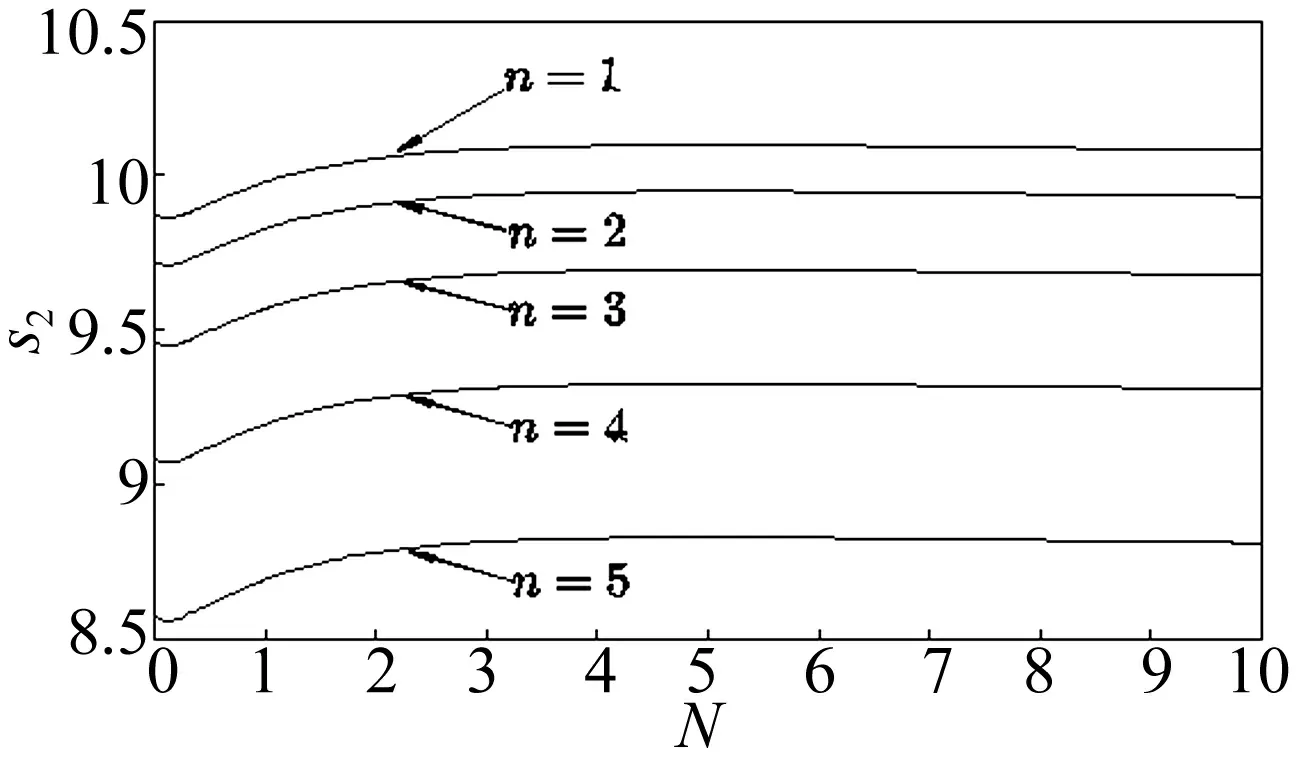
图1 周向波数n不同时内共振参数s2随梯度指数N变化

(9)

据Lagrange方程，得系统双模态控制方程为：

(10)

式中：ξ=k1/m2。

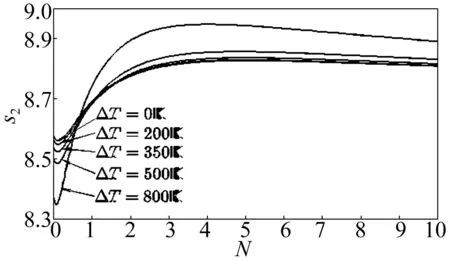
图2 ΔT不同时内共振参数s2随梯度指数N变化(n = 5)

2 多尺度分析

多尺度法为计算系统非线性模态的有效工具[13]，故采用多尺度法分析非线性模态方程式(10)。引入无量纲记号ε表征系统小参量，使q1→εq1，q2→εq2(ε仅为标记，实际计算中取ε≡ 1)，则式(10)变为：

(11)

其解可近似设为级数形式：

(12)

其中：T0=t,T1=εt。将式(12)代入式(11)化简并令ε同次幂系数为零得：

(13)

(14)

(15)

式中：A1，A2为复值函数；cc为各项共轭复数。

引入调谐参数σ，使ω2= 2ω1+εσ。将式(15)代入式(14)并消去永年项得：

(16)

为以极坐标形式表示调谐方程，设：

(17)

将式(17)代入式(16)并分离实、虚部，得模态坐标非线性调谐方程为：

(18)

式中：φ=β2-2β1+σT1。

式(18)存在两类不动点，分别对应于a1= 0及a1≠ 0。a1= 0不动点为：

(19)

a1≠ 0的两不动点分别为：

(20)

对不动点式(19)可求得其对应的三个特征值：

λ3=-2λ2

(21)

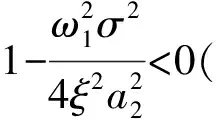
(22)

(23)

3 算例与结果讨论

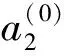
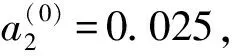
时尽管系统响应有差别，但均具有相似的定性性质，因此以下讨论中以n= 5时为例分析梯度指数与温度等因素对系统响应影响。

图3 不同周向波数n时a1频响曲线

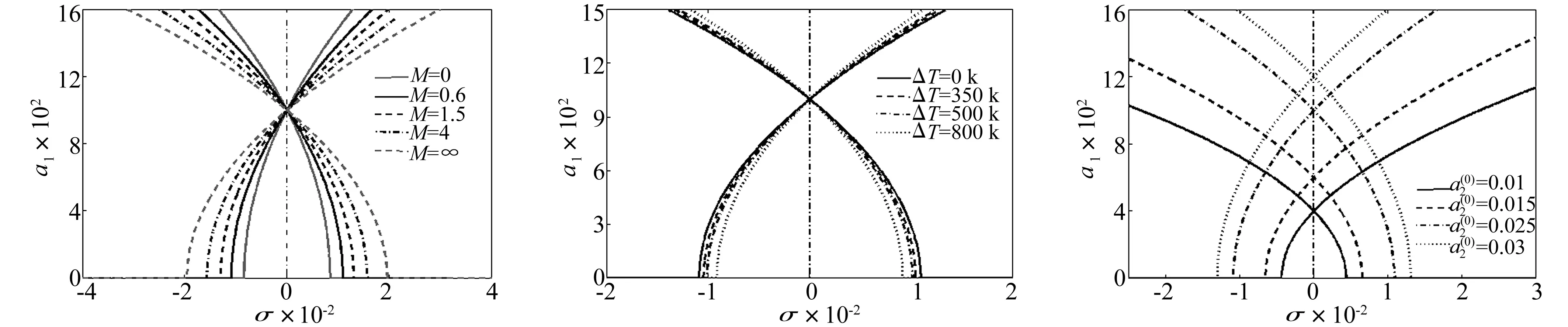
图4 不同梯度指数时a1频响曲线(ΔT = 0 k， a(0)2=0.025)

4 结 论

本文据文献[11]模型，采用多尺度法分析热环境中无限长FGM薄壁圆柱壳在发生内共振时的非线性模态运动，详细讨论梯度指数、温度变化及振动能量大小等因素对系统非线性模态频响特性影响。在FGM等效材料参数采用本文幂律分布规律描述的前提下，研究表明：

(1) 随调谐参数的变化，系统非线性模态会发生分岔；

(2) 调谐参数为零时，非轴对称模态振幅由轴对称模态的振动初值决定，与材料梯度指数及系统温度无关；

(3) 随梯度指数的增加调谐参数分岔值|σ|增大；随系统温度的增加分岔值|σcr|减小；

(4) 对特定的调谐参数值，轴对称模态单模态运动在低能状态为稳定运动，而在高能振动状态时变为不稳定运动。

参 考 文 献

[1]Birman V, Byrd L W. Modeling and analysis of functionally graded materials and structures[J]. Applied Mechanics Reviews, 2007, 60(5): 195-216.

[2]Loy C T, Lam K Y, Reddy J N. Vibration of functionally graded cylindrical shells[J]. International Journal of Mechanical Sciences, 1999, 41: 309-324.

[3]Yang J, Shen H S. Free vibration and parametric resonance of shear deformable functionally graded cylindrical panels[J]. Journal of Sound and Vibration, 2003, 261(5): 871-893.

[4]Malekzadeh P, Shahpari S A, Ziaee H R. Three-dimensional free vibration of thick functionally graded annular plates in thermal environment[J]. Journal of Sound and Vibration, 2010, 329(4): 425-442.

[5]黄小林, 沈惠申. 热环境下功能梯度材料板的自由振动和动力响应[J]. 工程力学, 2005, 22(3): 224-227, 81.

HUANG Xiao-lin, SHEN Hui-shen. Free vibration and dynamic response of functionally graded plates in thermal environments[J].Engineering Mechanics,2005,22(3):224-227.

[6]李世荣, 范亮亮. 热环境中功能梯度材料圆板的自由振动[J]. 振动工程学报, 2007, 20(4): 353-360.

LI Shi-rong, FAN Liang-liang. Free vibration of functionally graded circular plates in thermal environment[J]. Journal of Vibration Engineering, 2007, 20(4): 353-360.

[7]李清禄, 李世荣. 功能梯度材料梁在后屈曲构形附近的自由振动[J]. 振动与冲击, 2011, 30(9): 76-78.

LI Qing-lu, LI Shi-rong. Free vibration of FGM Euler beam with post-buckling configuration subjected to axial force[J]. Journal of Vibration and Shock, 2011, 30(9): 76-78.

[8]杜长城, 李映辉. 功能梯度矩形板的非线性自由振动[J]. 力学季刊, 2010, 31(2): 250-255.

DU Chang-cheng, LI Ying-hui. Nonlinear free vibration of functionally graded rectangular plates[J]. Chinese Quarterly of Mechanics, 2010, 31(2): 250-255.

[9]Alijani F, Amabili M, Karagiozis K, et al. Nonlinear vibrations of functionally graded doubly curved shallow shells[J]. Journal of Sound and Vibration, 2011, 330(7): 1432-1454.

[10]张志强, 胡宇达. 热环境中功能梯度圆板的非线性动力响应分析[J]. 复合材料学报, 2011, 28(6): 237-244.

ZHANG Zhi-qiang, HU Yu-da. Nonlinear dynamic response of circular functionally graded plate in thermal environment[J]. Acta Materiae Compositae Sinica, 2011, 28(6): 237-244.

[11]杜长城. 功能梯度薄壁圆柱壳的非线性模态相互作用与共振行为研究[D]. 成都: 西南交通大学, 2011.

[12]Vakakis A F. Analysis and identification of linear and nonlinear normal modes in vibrating systems[D]. California: California Institute of Technology, 1991.

[13]陈予恕, 吴志强. 非线性模态理论的研究进展[J]. 力学进展, 1997, 27(3): 2-13.

CHEN Yu-shu, WU Zhi-qiang. Advances in study on theories of nonlinear normal modes[J]. Advances in Mechanics, 1997, 27(3): 2-13.

[14]Avramov K V, Mikhlin Y V, Kurilov E. Asymptotic analysis of nonlinear dynamics of simply supported cylindrical shells[J]. Nonlinear Dynamics, 2007, 47: 331-352.

[15]Hunt G W, Williams K A J, Cowell R G. Hidden symmetry concepts in the elastic buckling of axially-loaded cylinders[J]. International Journal of Solids and Structures, 1986, 22(12): 1501-1515.