基于人工鱼群算法的轴承故障随机共振自适应检测方法
2014-09-05朱维娜
朱维娜, 林 敏
(中国计量学院 计量测试工程学院, 杭州 310018)
机械设备中滚动轴承应用广、易损坏。据统计,在用滚动轴承的旋转机械中,约有30%的机械故障由轴承引起。若不及时诊断轴承早期故障,将使机器设备产生严重故障,造成巨大经济损失。早期故障特征本身较微弱,实现早期故障微弱特征提取极具挑战性。现有提取方法多由消除噪声角度出发检测故障特征,如基于小波[1]、经验模式分解[2]、主分量分析[3]、局部均值分解[4]等降噪方法。然而对噪声重度污染的微弱特征信号,在降低噪声的同时也削弱了微弱特征信号,造成“两败俱伤”。随机共振[5]为利用噪声增强微弱特征信号的新理论。与传统方法相比其反其道而行之,在削弱噪声的同时强化微弱特征,能实现微弱特征的有效检测。对工程中待测信号及噪声未知情况,Mitaim等[6-7]提出自适应随机共振方法,能通过自动调节系统本身或其它相关参数实现对有用信号的检测。然而已有以系统单个参数为优化对象的自适应随机共振方法[8-9]忽略了随机共振系统中各参数间交互作用,实为局部寻优方法。采用遗传算法的自适应随机共振方法[8-9]能实现参数并行选择,全局寻优,然需涉及繁琐的编码过程,计算量较大,且种群数增多时算法收敛速度明显减缓。
随人工智能的发展,群智能算法作为其重要分支已在诸多领域得以应用[11-14],其用自适应概率搜索技术,由多点出发,具有进化性等优点,使其更容找到全局最优解。该优化算法主要包括粒子群算法、蚁群算法、人工鱼群算法。采用粒子群算法的自适应单稳系统随机共振成功实现冲击信号检测[15];采用蚁群算法的自适应随机共振在机械故障信号检测领域得以初步应用[16];利用群智能算法的自适应随机共振发展前景广阔。
本文据人工鱼群算法对初值、参数设定容许范围大及能克服局部极值、获取全局极值的能力,选双稳系统输出信噪比作为适应度函数,对产生随机共振的双稳系统参数进行同步优化,准确快速找到最优参数,使随机共振效应最强烈,实现微弱特征检测及早期故障诊断。
1 基本理论
1.1 随机共振
实现随机共振基本三要素为:微弱输入信号、噪声、非线性系统。随机共振模型由非线性朗之万方程描述:
式中:s(t)=Acos(ωt)为某微弱周期信号(幅值A≪1),Γ(t)为零均值高斯白噪声,满足条件E[Γ(t)Γ(t+τ)]=2Dδ(t-τ);D为噪声强度。
传统的随机共振模型为双稳随机共振,势函数为:
在随机共振系统中,影响跃迁的主要因素为势垒高度ΔU,而系统参数a,b共同决定ΔU的大小。a,b对能否产生随机共振起决定性作用。当ΔU太小时随机共振效果不明显;太大时无法产生随机共振。因此,对不同输入信号必存在一对最优参数a,b可产生合适的ΔU,使随机共振效果最明显。
1.2 人工鱼群算法
人工鱼群算法(Artificial Fish Swarm Algorithm,AFSA)由李晓磊[17]提出。利用鱼觅食、聚群、追尾行为,从构造单条鱼简单底层行为起,通过鱼群中个体局部寻优行为,在群体中突现全局最优值。
1.2.1 人工鱼模型定义

1.2.2 觅食、聚群、追尾行为
觅食行为:设人工鱼当前状态为Xi,在其可见域内随机选择一状态Xj,该状态食物浓度大于当前状态时,则向该方向前进一步;反之则重新随机选状态Xj,判断是否满足前进条件;反复几次后,若环境仍不满足前进条件,则随机移动一步。
聚群行为:人工鱼当前状态为Xi,探索当前邻域内(即di,j≤Visual)内伙伴数目为nf及中心位置Yc,若Yc/nf>δYi且Yi 追尾行为:人工鱼当前状态为Xi,探索可见域内所有伙伴中适应度值最大伙伴Xj,若Yj/nf>δYi且Yi 1.2.3 行为评价 据需解决问题的性质,对人工鱼当前所处环境进行评价,选择一种行为。缺省行为为觅食行为。 1.2.4 公告板更新 算法中设立一公告板,每条人工鱼在行动一次后,将自身当前状态食物浓度与公告板比较,优于公告板则用自身状态取代公告板状态,使公告板记录历史最优状态。 1.2.5 终止条件判定 算法终止条件可据问题性质或要求而定。如通常为判断连续多次所得值均方差小于允许误差,或判断聚集于某区域的人工鱼数目达到某比率或限制最大迭代次数等方法。满足终止条件,输出公告板最优记录;否则,继续迭代。 随机共振效应可通过输出信噪比大小衡量。输出信噪比SNRout=10log(S(ω0)/N(ω0))达最大值max(SNR)时,系统处于最佳随机共振状态。其中,S(ω0)为信号功率谱;N(ω0)为噪声在信号频率附近的平均功率谱。基于人工鱼群算法的随机共振信号检测方法以输出信噪比作为随机共振效应评价函数,利用人工鱼群算法的并行机制,对随机共振系统参数进行同步优化,搜寻使信噪比达最大值时的系统参数a,b最优值,使随机共振达最佳效果,自适应实现微弱信号检测。具体步骤如下: (1) 设定人工鱼群算法参数。鱼群规模N,最大迭代次数m,人工鱼感知范围Visual,最大移动步长Step,拥挤度因子δ等。 (2) 初始化鱼群。分别确定系统参数a,b的寻优范围,在该范围内随机生成第k=0代人工鱼群体,规模N作为初始鱼群。 (3) 计算初始鱼群中人工鱼个体当前位置的食物浓度值Y=FC(x)(其中食物浓度大小即对应适应度函数信噪比高低),比较大小,取最大值者进入公告板,将此鱼赋值给公告板。 (4) 每条人工鱼模拟追尾行为、聚群行为。选择Y值较大的行为执行。缺省行为为觅食行为。 (5) 每条人工鱼行动一次后,检验自身食物浓度Y值与公告板Y值。若优于公告板,则以自身取代,使公告板始终保持较大值。 (6) 若满足结束条件(达最大迭代次数m),转(7);否则转入(4)。 (7) 输出公告板最优记录,即信噪比达最大值时a,b最优值。将优化所得系统参数a,b代入随机共振系统形成自适应优化系统,使其实现微弱信号检测。 图1 采用人工鱼群算法的系统参数优化流程 通过数值仿真分析基于人工鱼群算法自适应随机共振的有效性,设周期信号s(t)=Asin(2πf0t),其中幅值A=0.3,频率f0=0.01 Hz。在信号中加入零均值的高斯白噪声,噪声强度D=0.31,数据长度L=8 000,采样频率fs=5 Hz。图2为输入输出信号时域波形及功率谱图。 采用传统的自适应随机共振方法分析仿真信号,即固定一个参数,调节另一个参数以增强随机共振效果。固定系统参数a,在[0.1 10]范围内调节参数b,得b=3.201时输出信噪比最大,为SNR=43.248 5。利用人工鱼群算法并行优化随机共振两系统参数a、b,在系统能产生随机共振前提下,初始化a、b范围为[0.000 01 2]、[0.1 10],人工鱼移动步长0.1,感知距离Visual为2.5,拥挤度因子δ为0.618,迭代500次寻找随机共振系统最佳参数组合。优化结果为a=0.952 0,b=2.017 4。将系统参数设为最优参数产生随机共振,得输出信噪比SNR=48.534 5;而利用单个参数为优化对象的自适应随机共振所得输出信噪比SNR=43.248 5。由此,基于人工鱼群算法的自适应随机共振所得信噪比较传统方法增大12%。由图2~图4知,传统的自适应随机共振系统的输出在时域上呈现周期性,频域上特征频率处出现较输入信号明显的谱峰值现象。但基于人工鱼群算法的自适应随机共振系统输出在频域上较传统方法特征频率更突出,有利于噪声重度污染的微弱特征信号检测。 图2 系统输入时域波形及功率谱 图5为型号N/NU 205EM的轴承滚动体故障。该轴承参数为:滚动体直径Bυ=7.5 mm,滚道节径PD=65 mm,内径Ra=25 mm,外径Rb=52 mm,滚动体个数N=12,接触角β=0°。实验中采集轴承加速度信号,采样频率80 kHz,采样长度1 048 640点,转速1 500 r/min。据相关公式,得该轴承滚动体故障特征频率为125.18 Hz。图6为轴承故障信号时域波形及功率谱图,由图6知,时域信号中背景噪声强烈,轴承故障的特征成分被完全淹没,信噪比极低,在轴承故障特征频率处不能检测到明显谱峰。 随机共振理论要求输入信号满足小参数条件,因此对不满足小参数条件的工程实测信号进行参数优化之前需预处理。可通过二次采样[18]实现,再用随机共振方法提取微弱特征。对实测故障信号预处理,使其满足产生随机共振的小参数条件,设定频率压缩比为R=5 000,二次采样频率变为fst=80 000/5 000=16 Hz,即数值仿真计算步长h=1/fsr=1/16 s。设系统参数a,b范围为[0.000 01 20]、[0.1 20],人工鱼移动步长为0.1,感知距离Visual为2.5,拥挤度因子δ为0.618,迭代600次寻找随机共振系统最佳参数组合。优化结果为a=10.633 5,b=18.925 2。将系统参数设为最佳参数产生随机共振,获得输出信噪比SNR=31.448 3,且在频率fr0=0.025 02处存在较突出频率分量,据频率压缩比还原,轴承故障基本频率为f0=fr0R=0.025 02×5 000=125.10 Hz。由轴承滚动体引起的故障频率理论值为125.18 Hz。由图7可知,滚动体故障特征频率处功率谱值较周围成分高出很多,在整个功率谱中较突出,而在原始信号功率谱图中完全不能检测到故障特征频率对应的谱峰值。 图5 轴承滚动体故障 图7 人工鱼群算法自适应随机共振系统输出时域波形及功率谱图 采用传统自适应随机共振方法对同样信号进行分析知,固定参数a=1,在参数初始化范围内遍历搜索参数b,使输出信噪比最大时b的优化结果为b=1.502 0,输出信号时域图及功率谱图见图8。与图7、图6对比可知,采用传统自适应随机共振方法几乎未检测到滚动体故障特征频率。但人工鱼群算法自适应随机共振谱峰值明显且增加24%。原因在于传统自适应随机共振以单个系统参数为优化对象,忽略了参数间交互作用,优化所得随机共振参数仅为局部最优解;而采用人工鱼群算法的自适应随机共振则充分利用人工鱼群算法全局搜索、并行处理能力,对随机共振系统参数a,b进行同步优化,考虑参数间交互作用,优化所得随机共振参数则为使信噪比达最大值的全局最优解,随机共振效应最强烈,实现了强噪声背景下轴承滚动体故障信号检测。因此,基于人工鱼群算法的轴承故障随机共振自适应检测方法最有效。 利用人工鱼群算法搜索过程的灵活性及对搜索空间的自适应能力,以信噪比为适应度函数,对随机共振系统结构参数进行同步优化,实现了对原始信号中微弱周期成分的最优提取。该方法能克服已有自适应随机共振单个参数优化选择及采用遗传算法编码复杂、种群增多时收敛速度减缓的自适应随机共振缺点,能快速、有效实现系统参数的并行选择及优化。数值仿真与轴承故障诊断实例验证了基于人工鱼群算法的自适应随机共振方法在故障诊断中的有效性。 参 考 文 献 [1]孙 伟,熊邦书,黄建萍,等. 小波包降噪与LMD相结合的滚动轴承故障诊断方法[J]. 振动与冲击, 2012, 31(18): 153-156. SUN Wei, XIONG Bang-shu, HUANG Jian-ping, et al. Fault diagnosis of a rolling bearing using Wavelet packet de-noising and LMD[J]. Journal of Vibration and Shock, 2012, 31(18): 153-156. [2]蔡艳平, 李艾华, 石林锁, 等. 基于EMD与谱峭度的滚动轴承故障检测改进包络谱分析[J]. 振动与冲击, 2011, 30(2): 167-172. CAI Yan-ping, LI Ai-hua, SHI Lin-suo, et al. Roller bearing fault detection using improved envelope spectrum analysis based on EMD and spectrum kurtosis[J]. Journal of Vibration and Shock, 2011, 30(2): 167-172. [3]成 玮, 张周锁, 何正嘉, 等. 基于独立分量分析的潜艇振源贡献量定量计算方法[J]. 机械工程学报,2010,46(7): 82-87. CHENG Wei, ZHANG Zhou-suo, HE Zheng-jia, et al. Quantitative calculation of vibration source contributions of submarines based on independent component analysis[J]. Journal of Mechanical Engineering, 2010, 46(7): 82-87. [4]陈亚农, 郜普刚, 何 田, 等. 局部均值分解在滚动轴承故障综合诊断中的应用[J]. 振动与冲击, 2012, 31(3): 73-78. CHEN Ya-nong, GAO Pu-gang, HE Tian,et al. Roller bearing comprehensive fault diagnosis based on LMD[J]. Journal of Vibration and Shock, 2012, 31(3): 73-78. [5]Benzi R, Sutera A, Vulpinai A. The mechanism of stochastic resonance[J]. Journal of Physics A: Mathematical and General, 1981, 14(11): 453-457. [6]Mitaim S, Kosko B. Adaptive stochastic resonance[J]. Proceedings of the IEEE, 1998, 86(11): 2152-2183. [7]LI Jian-long, XU Bo-hou. Effects of signal spectrum varying on signal processing by parameter-induced stochastic resonance[J]. Physica A: Statistical Mechanics and its Applications, 2006, 361(1): 11-23. [8]LI Qiang, WANG Tai-yong, LENG Yong-gang, et al. Engineering signal processing based on adaptive step-changed stochastic resonance[J]. Mechanical Systems and Signal Processing, 2007, 21(5): 2267-2279. [9]谭继勇, 陈雪峰, 雷亚国, 等. 自适应移频变尺度随机共振在故障诊断中的应用[J]. 西安交通大学学报, 2009, 43(7): 69-73. TAN Ji-yong, CHEN Xue-feng, LEI Ya-guo, et al. Adaptive frequency-shifted and re-scaling stochastic resonance with applications to fault diagnosis [J]. Journal of Xian Jiaotong University,2009, 43(7): 69-73. [10]王 晶, 张 庆, 梁 霖, 等. 采用遗传算法的自适应随机共振系统弱信号检测方法研究[J]. 西安交通大学学报, 2010, 44(3): 32-36. WANG Jing, ZHANG Qing, LIANG Lin, et al. Adaptive stochastic resonance based on genetic algorithm with applications in weak signal detection[J]. Journal of Xian Jiaotong University,2010, 44(3): 32-36. [11]Teodorovic D. Swarm intelligence systems for transportation engineering: principles and applications [J]. Transportation Research Part C, 2008, 16(6): 651-667. [12]Bernardino E M, Bernarno A M, Sanches-Perez J M, et al. Swarm optimisation algorithms applied to large balanced communication networks[J]. Journal of Network and Computer Applications, 2013, 36(1): 504-522. [13]SHEN Wei, GUO Xiao-peng, WU Chao,et al. Forecasting stock indices using radial function neural networks optimized by artificial fish swarm algorithm[J]. Knowledge-Based Systems, 2011, 24(3): 378-385. [14]陈安华, 周 博, 张会福, 等. 基于改进人工鱼群算法的机械故障聚类诊断方法[J]. 振动与冲击, 2012, 31(17): 145-148, 158. CHEN An-hua, ZHOU Bo, ZHANG Hui-fu, et al. A clustering method for mechanical fault diagnosis based on improved fish-swarm algorithm[J]. Journal of Vibration and Shock, 2012, 31(17):145-148,158. [15]李继萌, 陈雪峰, 何正嘉. 采用粒子群算法的冲击信号自适应单稳态随机共振检测方法[J]. 机械工程学报, 2011, 47(21): 58-63. LI Ji-meng, CHEN Xue-feng, HE Zheng-jia. Adaptive monostable stochastic resonance based on PSO with application in impact signal detection[J]. Journal of Mechanical Engineering, 2011, 47(21): 58-63. [16]雷亚国, 韩 冬, 林 京, 等. 自适应随机共振新方法及其在故障诊断中的应用[J]. 机械工程学报, 2012, 48(7): 62-67. LEI Ya-guo, HAN Dong, LIN Jing, et al. New adaptive stochastic resonance method and its application to fault diagnosis[J]. Journal of Mechanical Engineering, 2012, 48(7): 62-67. [17]李晓磊, 邵之江, 钱积新. 一种基于动物自治体的寻优模式: 鱼群算法[J]. 系统工程理论实践, 2002, 22(11): 32-38. LI Xiao-lei, SHAO Zhi-jiang, QIAN JI-xin. An optimizing method based on autonomous animals: fish-swarm algorithm [J]. Systems Engineering-Theory & Practice, 2002, 22(11): 32-38. [18]冷永刚, 王太勇. 二次采样用于随机共振从强噪声中提取弱信号的数值研究[J]. 物理学报, 2003, 52(10): 2432-2437. LENG Yong-gang, WANG Tai-yong. Numerical research of twice sampling stochastic resonance for the detection of a weak signal submerged in a heavy noise[J]. Journal of Physics, 2003, 52(10): 2432-2437.2 人工鱼群算法的自适应随机共振

3 数值仿真结果与分析
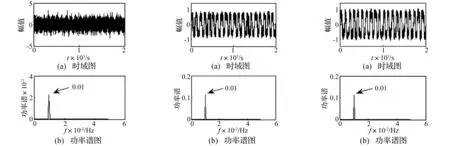
4 工程应用


5 结 论
