基于Tikhonov正则化及奇异值分解的载荷识别方法
2014-09-05房怀庆于钦林朱伟伟
郭 荣, 房怀庆, 裘 剡, 于钦林, 朱伟伟
(1.同济大学 中德学院,上海 201804; 2.同济大学 汽车学院,上海 201804; 3.同济大学 汽车新能源汽车工程中心,上海 201804)
传递路径分析方法[1-3](Transfer Path Analysis, TPA)为机械系统振动噪声常用诊断手段,广泛用于汽车、航空航天、潜艇等领域。TPA主要通过估计噪声源及各传递路径的贡献率,找出对响应影响较大的声源及传递路径,其中载荷识别精度对各传递路径贡献量影响显著。
载荷识别为结构动力学难点之一,而频响函数求逆法在工程实际中使用较广。Schevenels等[4-6]利用结构动力学关系构建载荷识别动力学方程,并提出通过频响函数求逆法进行载荷识别,用奇异值分解法(Singular Value Decomposition,SVD)改善声源识别中频响函数求逆的病态问题。Choi等[7-8]运用Tikhonov正则化方法,提高载荷识别结果稳定性,并分析对比不同正则化参数选择方法对载荷识别精度影响。目前研究采用SVD法、Tikhonov正则化法虽可提高载荷识别精度,并未比较两方法间的优缺点及系统病态性不同时两种方法的适用性。对此,本文提出基于Tikhonov正则化与奇异值分解的载荷识别方法,考虑系统病态性对载荷识别影响,用频响函数法矩阵条件数评价系统的病态性,通过平板模型仿真分析,在频域运用奇异值分解法与基于普通交叉验证法(Ordinary Cross Validation,OCV)、广义交叉验证法(Generalized Cross Validation,GCV)、L曲线法(L-curve)三种不同正则化参数选择方法的Tikhonov正则化法进行载荷识别,分析总结系统病态性不同时,不同方法载荷识别精度及适用性。通过简支梁台架载荷识别实验,验证该方法的可行性。
1 结构载荷识别方法
TPA方法假设机械系统某目标响应位置的结构噪声可由各传递路径产生的贡献分量相加[1]:
(1)
式中:p为目标响应点处总声压;Hij为传递路径i在j方向频率响应函数(Frequency Response Function,FRF);Fj为系统中第j位置施加的激励。由式(1)知,若求出目标点总声压,则须先获得各条路径的频响函数及工作载荷,其中结构载荷识别精度对各路径声压贡献量影响较大。
工程中常采用频响函数求逆法识别工作载荷。设待识别工作载荷数目为s,实测响应点位置数为n,响应点数n与工作载荷数目s通常不相等,故频率响应函数的逆为广义逆[9]:
(2)
其中:a为响应点响应;H+为频响函数H的广义逆。
由式(2),频响函数求逆法应用的关键在于解决其可能存在的病态逆问题。若系统病态性严重,即使较小测量误差也会被放大。该病态问题可用方法以改善,其中奇异值分解法因计算简便应用最广[4-6];而Tikhonov正则化法求解稳定性良好,亦获得应用[7-8]。
2 奇异值分解法

(3)
将式(3)代入式(2)可得奇异值分解法对载荷识别的表达式[5]:
F=VS-1UHa
(4)
3 正则化方法
3.1 Tikhonov正则化理论
测量方法所限,所测响应a及频率响应函数H均存在误差。为控制及度量误差,设整系统绝对误差为:
e=a-HF
(5)
为使误差e尽量小,Tikhonov引入罚函数[10]:
J=(eHe)+λ(FHF)
(6)
当J对F的一阶导为零时,误差e存在最小值,则可得F:
F=(HHH+λI)-1HHa
(7)
其中:I为单位阵;λ为正则化参数。λ等于零时,上述解即为最小二乘解;λ趋向无穷大时,解为零向量。如何选择正则化参数λ是正则化算法的关键。正则化参数λ选择方法主要有普通交叉验证法、广义交叉验证法及L曲线法。
3.2 正则化参数选择方法
3.2.1 OCV法
在OCV方法中,通过式(7)求得激振力F,并代入式a=HF中求得响应,比较所求响应与实际响应间差别,OCV可定义为[8]:
(8)

3.2.2 GCV法
定义对角化循环酉矩阵W:
(9)
用循环酉矩阵W与某矩阵相乘,即对该矩阵进行离散傅里叶变换,可用此解决FRF对角化问题。由绝对误差:
e=a-HF=a-USVHF
(10)
式(10)两边同乘WUH,得:
et=at-HtF
(11)
其中:et=WUHe;at=WUHa;Ht=WSUH。对式(11)用OCV法理论可得GCV法表达式为[6,11]:
(12)
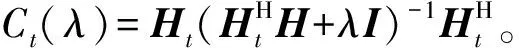
3.2.3L曲线法
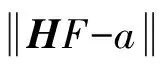
(13)
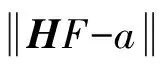
4 平板模型仿真分析
4.1 仿真模型建立
研究在系统病态性情况不同时,采用基于OCV法、GCV法、L曲线法不同正则化参数选择的Tikhonov方法及SVD法的载荷识别精度及此方法具体的适用性,利用Patran、Nastran进行仿真分析。仿真中,用600×500×1.5 mm钢板,弹性模量E=2.07×1011N/m2,泊松比μ=0.3,结构阻尼0.06。在板上随机选择激励及响应点位置,尽量避免边界位置[4]。由于钢板厚度相对长宽非常小,故可将问题弱化为平面问题[13],采用壳单元,单元厚度1.5 mm。简支矩形板约束为:[Ux,Uy,Uz]=[0,0,0], [Rx,Ry,Rz]=[0,0,1](“0”为约束该自由度;“1”为不约束该自由度,在Patran中设置为空格),网格大小控制为0.01 m,共有节点3 111个、单元3 000个。对有预约束的平板模型进行模态分析,获得平板前10阶固有频率,见表1。通过4次在不同位置施加单位激励进行频响分析,可确定激励点及响应点间频响函数。第5次在不同位置同时施加一定大小激励,进行频响分析,获得响应点加速度响应用于识别所加激励。仿真中施加激振力及响应点位置见表2。考虑结构载荷频率范围,频响分析范围设为10~250 Hz。
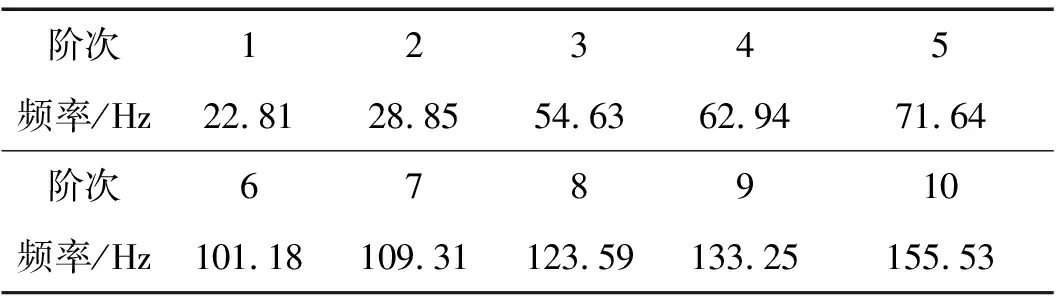
表1 平板前10阶固有频率
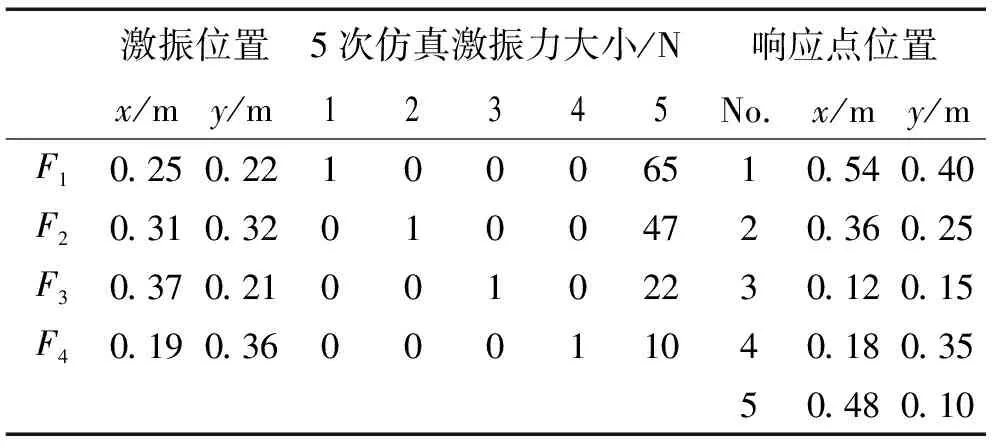
表2 激励幅值、坐标及响应位置坐标
4.2 噪声模型
响应点加速度测量及激振力施加会存在噪声干扰,因此需在仿真数据中引入不同信噪比(SNR)噪声。噪声用可加性高斯白噪声,其模型为:
N(ω)=Nndej2πNud
(14)
其中:Nnd为正态分布随机数,均值0,方差A(ω)10-(B/20)(A(ω)为加速度响应,B为信噪比);Nud为0~1均匀分布随机数。考虑实际情况,在频响函数中分别加入40 dB,22 dB信噪比等级噪声,在响应中分别加入40 dB,22 dB,15 dB,10 dB信噪比噪声,探讨不同噪声等级下基于不同正则化参数选择的Tikhonov方法与SVD法的载荷识别精度。
4.3 不同噪声等级下系统病态性
频响函数测量误差会直接影响系统的病态性,而在数据处理中病态性危害较大,会造成结果失真,若系统严重病态,即使测量中极小误差也会在数据处理过程中被放大。一般采用频响函数法矩阵条件数度量系统的病态性。设频率响应函数矩阵法矩阵HHH的条件数为K,统计经验表明[14]:0
4.4 采用不同逆问题解法载荷识别结果
为讨论系统病态性不同时采用不同逆问题解法的载荷识别结果差异,以频响函数中含22 dB噪声、响应中含15 dB噪声为例,用不同逆问题解法的载荷识别结果见图2。

图1 系统在不同噪声等级下病态情况
由图1、图2看出:
(1) 误差较大处均在条件数>1 000区域,即系统病态区域,且均在系统固有频率处,其中第一阶固有频率误差最大(图1)。
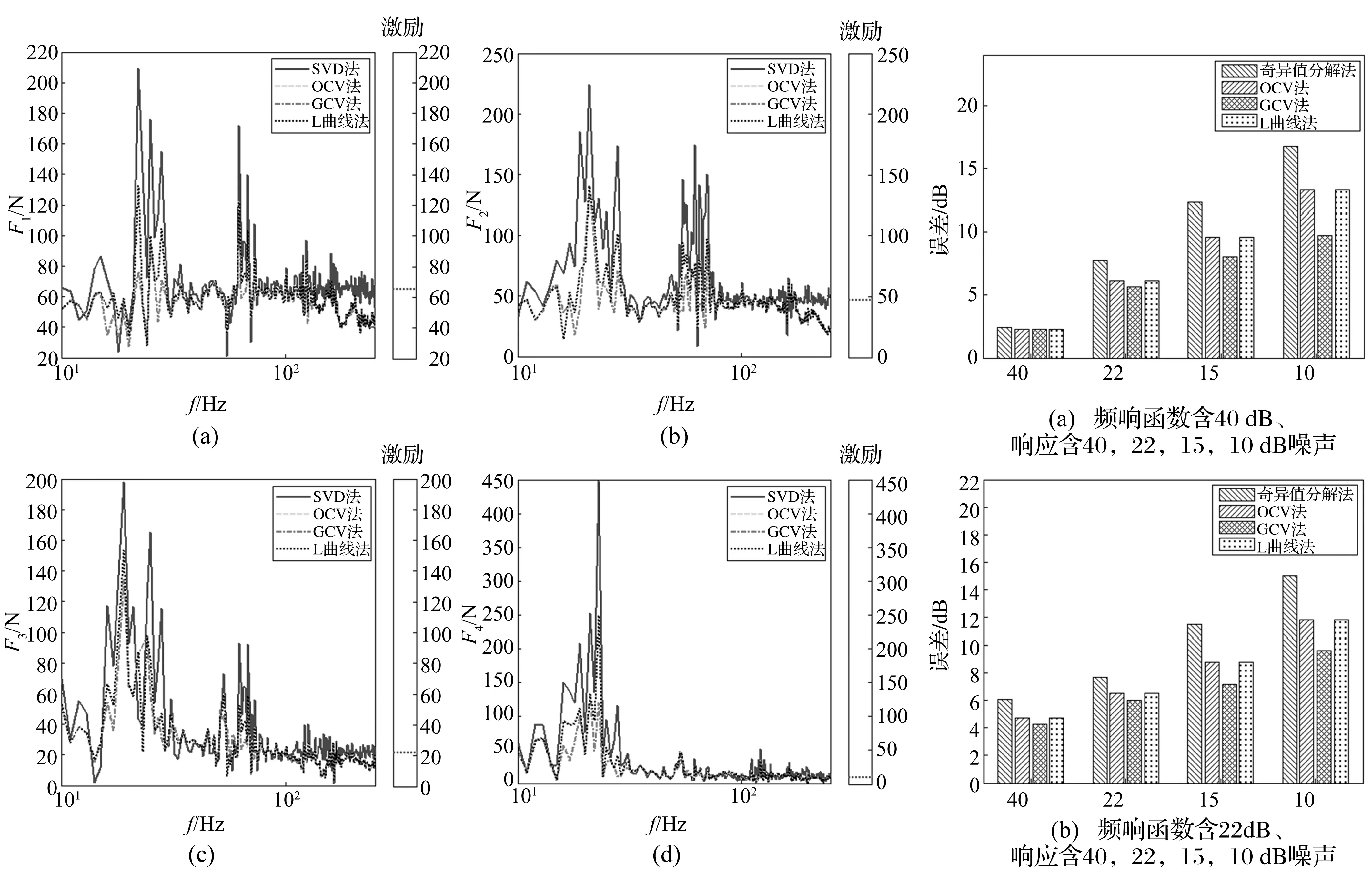
图2 频响函数中含22 dB噪声、响应中含15 dB噪声时载荷识别结果
(2) 在一阶固有频率附近,用不同正则化参数选择的Tikhonov正则化法载荷识别精度普遍优于SVD法(图2)。
(3) 在100~250 Hz频率范围内,条件数相对较小,与实际激励相比,SVD法较Tikhonov正则化方法识别的载荷精度更好。
为定量分析不同载荷识别方法误差,定义误差计算表达式为:
(15)
其中:FRf为识别激励;FTf为施加激励;N为采集数据点数;n为待识别激励数目;εforce单位dB。以频响函数法矩阵条件数1 000为基准,条件数>1 000时,SVD法及基于不同正则化参数选择的Tikhonov方法在不同噪声等级下载荷识别误差见图3;条件数≤1 000时,SVD法与基于不同正则化参数选择的Tikhonov方法在不同噪声等级下载荷识别误差见图4。
由图3、图4看出:
(1) 条件数>1 000时,Tikhonov正则化方法相较SVD法可有效降低载荷识别误差,其中基于OCV法与L曲线法正则化参数选择的Tikhonov方法载荷识别误差相差不大,而GCV法误差最小。
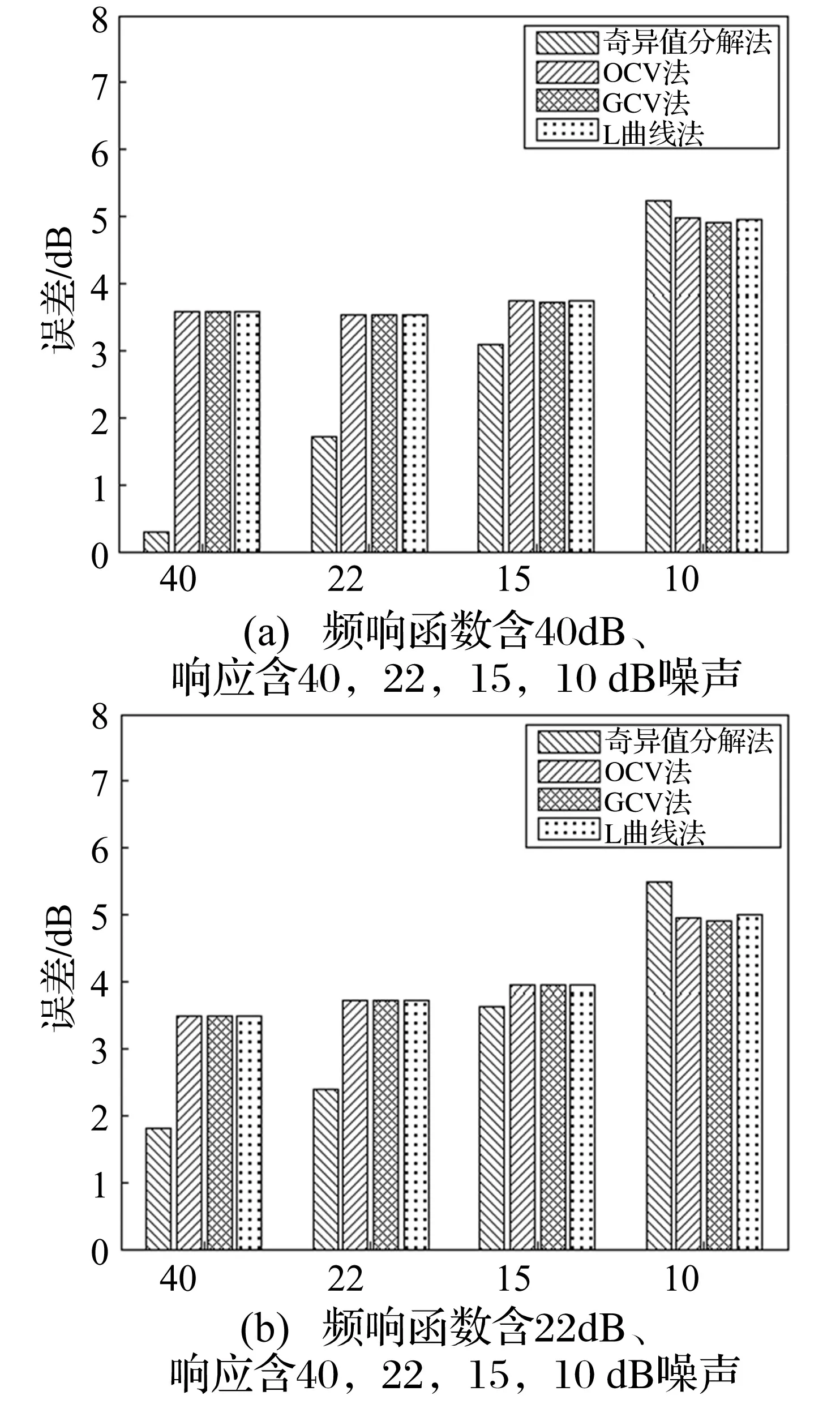
图4 条件数小于等于1 000时SVD法和基于不同正则化参数选择的Tikhonov方法的识别误差
(2) 条件数≤1 000时,基于三种正则化参数选择的Tikhonov方法载荷识别误差相差不大,而SVD法除响应中含10 dB高噪声外,载荷识别误差最小。响应中10 dB信噪比噪声在实际中较高,高噪声时SVD法的识别精度无Tikhonov正则化方法好。
5 基于Tikhonov法及SVD法的载荷识别方法
由以上分析知,系统严重病态(条件数>1 000)时,Tikhonov正则化法识别载荷精度较好,其中GCV选择正则化参数精度最高;条件数≤1 000时,SVD法识别载荷误差较小。为此,提出基于Tikhonov正则化方法与SVD法的载荷识别新方法。该方法以频响函数法矩阵条件数为依据,条件数≤1 000时,采用SVD法识别载荷;条件数>1 000时,采用Tikhonov正则化方法识别载荷,以GCV法选择正则化参数为例,对基于Tikhonov法与SVD法的载荷识别流程进行说明,见图5。
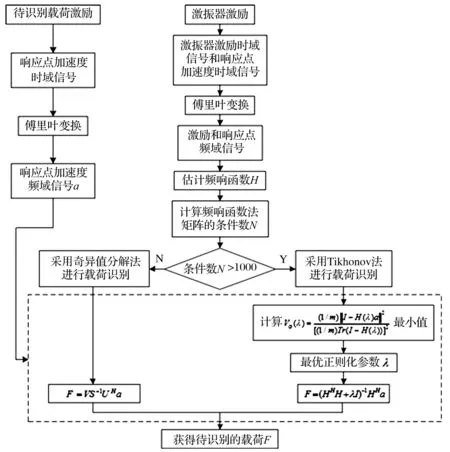
图5 方法流程图
采用新的基于Tikhonov正则化方法与SVD法的载荷识别方法与单独用SVD法和Tikhonov正则化识别误差对比见图6。由图6看出:①响应中含40 dB、22 dB、15 dB噪声时,新方法明显较单独用SVD法与Tikhonov正则化方法识别载荷精度高;②响应中含10 dB高噪声时,新方法载荷识别精度明显优于SVD法,但较Tikhonov方法略差。原因在于高噪声时SVD识别误差较大,导致新方法识别精度下降。与单独用SVD法及Tikhonov方法相比,新方法在不同等级噪声下均可取得较好载荷识别精度。
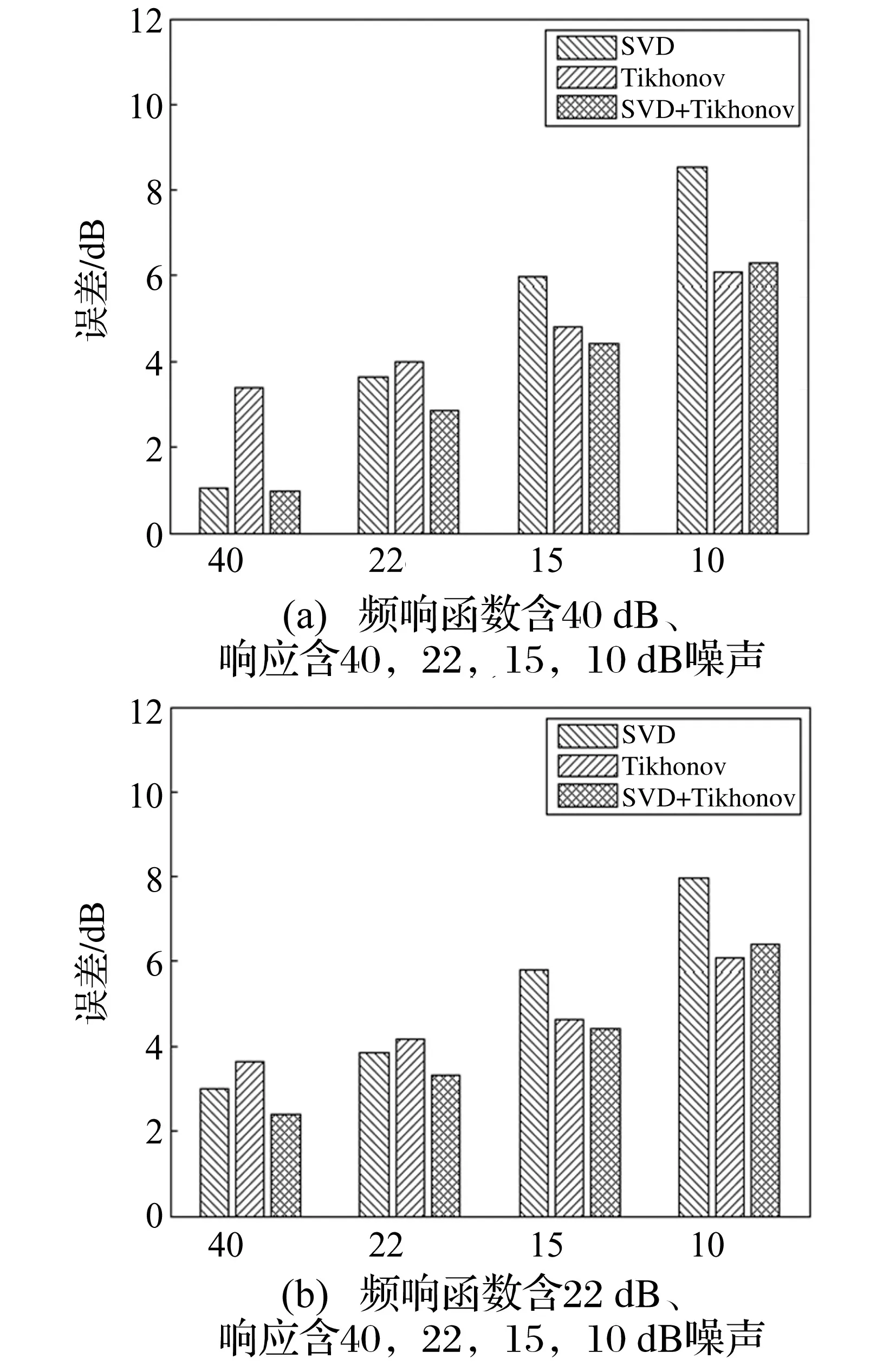
图6 SVD法、Tikhonov正则化方法与新方法载荷识别误差
6 载荷识别实验验证
实验用两端简支矩形梁,采用YE15400电动式激振器激励同时三点激励,激励信号为随机触发,测量四点加速度响应,数采LMS SCADAS Ⅲ 316,分析范围25~800 Hz。简支梁长、宽、高为:640 mm、56 mm、8 mm,模态分析获得简支梁前四阶固有模态见表3。共进行三组实验,实验框图见图7,实验台架见图8。

表1 简支梁前四阶固有频率
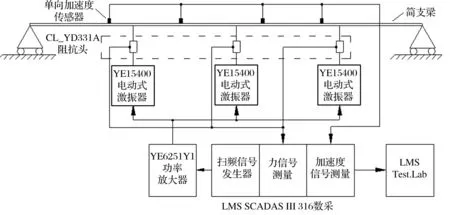
图7 实验框图

图8 实验台架
实验获得频响函数法矩阵条件数见图9。由图9看出,第一阶固有频率处条件数最大。
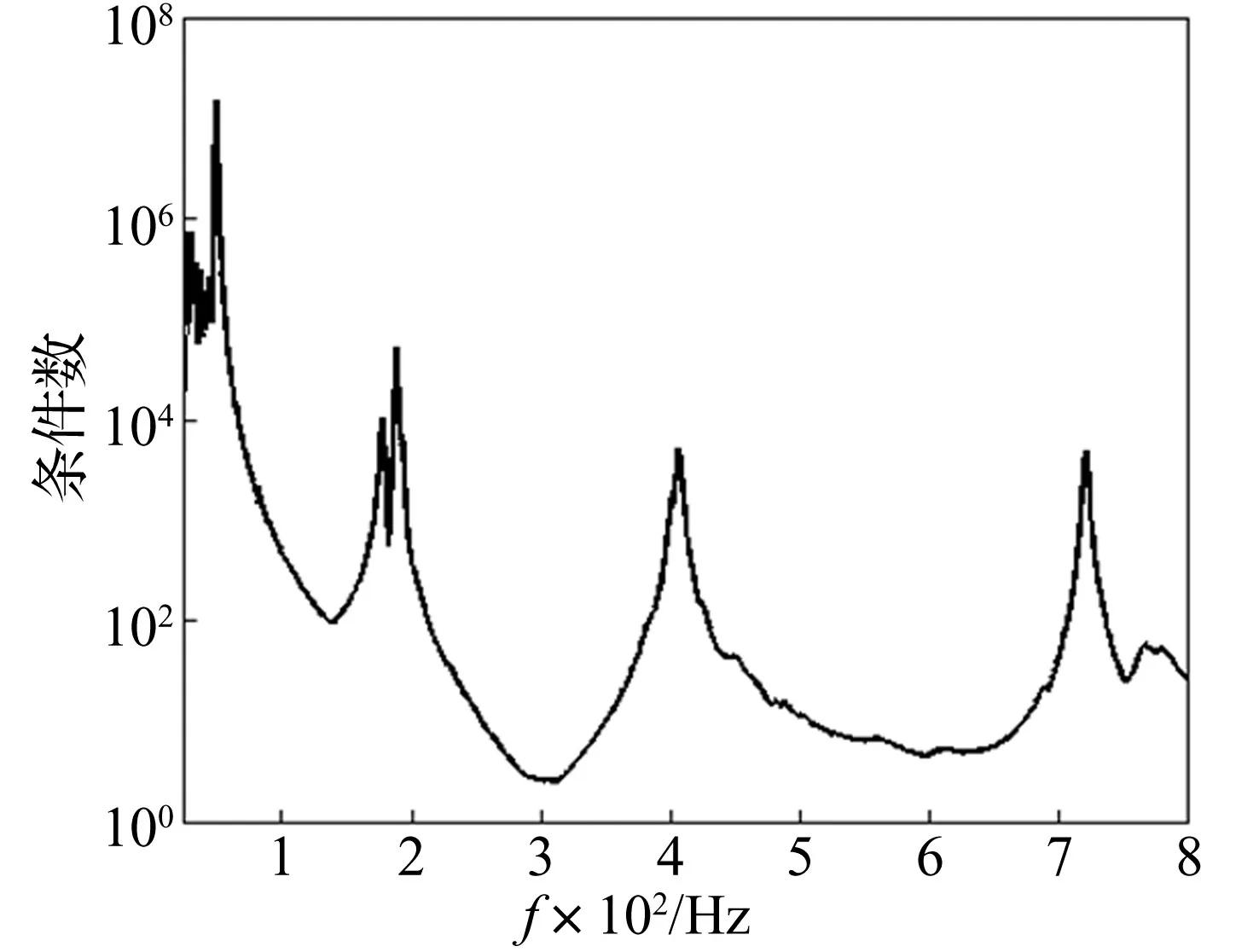
图9 频响函数法矩阵条件数
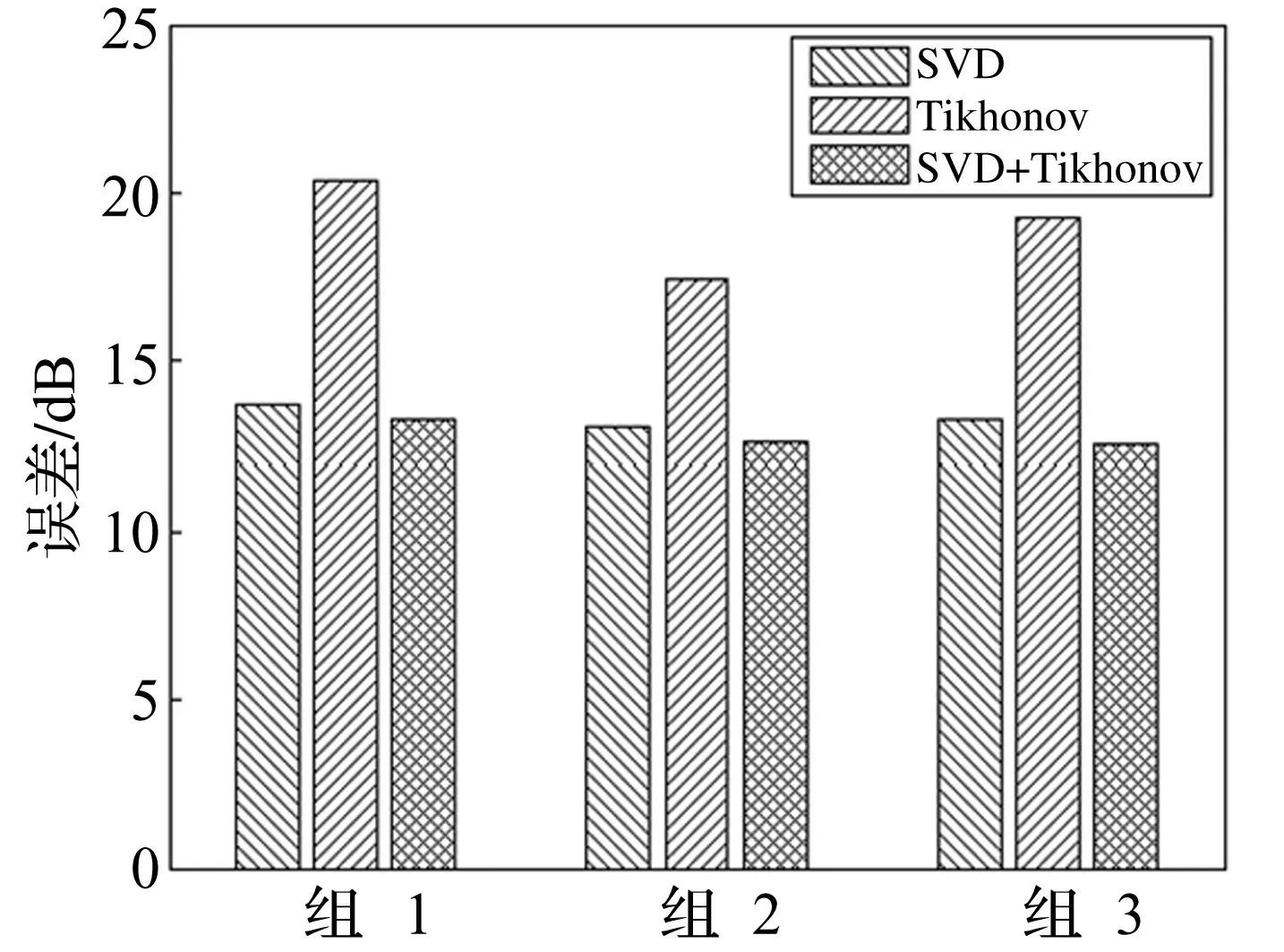
图10 SVD法、Tikhonov正则化方法与新方法载荷识别误差
采用新的基于Tikhonov正则化方法与SVD法载荷识别方法与单独用SVD法及Tikhonov正则化识别误差对比见图10。由图10看出,新方法可提高载荷识别精度。
7 结 论
本文采用Tikhonov正则化与SVD法解决病态逆问题。通过仿真讨论系统病态性情况不同时,采用基于OCV法、GCV法、L曲线法不同正则化参数选择的Tikhonov方法及SVD法载荷识别精度具体适用性,据频响函数法矩阵条件数,提出综合使用Tikhonov正则化法及SVD法的新载荷识别方法,结论如下:
(1) 载荷识别误差较大处均在条件数>1 000处,即系统病态区域,且均在系统固有频率处,其中第一阶固有频率误差最大;
(2) 条件数>1 000,相比SVD法,采用Tikhonov方法的载荷识别误差较小,其中采用GCV法选择正则化参数精度最高;当条件数≤1 000时,SVD法载荷识别精度较好;
(3) 由仿真、实验研究发现,与单独采用SVD法及Tikhonov方法相比,综合使用Tikhonov正则化法与SVD法可有效提高载荷识别精度。
本文研究结论以期为动力学病态逆问题解决提供参考。
参 考 文 献
[1]郭 荣,万 钢,赵燕男,等.车内噪声传递路径分析方法探讨[J].振动、测试与诊断,2007(3):199-203.
GUO Rong, WAN Gang, ZHAO Yan-nan,et al. Study on transfer path analysis method of automobile interior noise[J]. Journal of Vibration, Measurement and Diagnosis, 2007(3): 199-203.
[2]Vecchio A, Valent L, Carluccio L,et al. Experimental noise transfer path analysis on the helicopter A109[C]. National Aerospace Laboratory NLR-32nd European Rotorcraft Forum, ERF,Aerospace Societies,2007:197-210.
[3]Pieter S,Van der Linden P J G. An inverse force measurement method to determine the injected structure-borne sound power from an installation into a building element[J]. Building Acoustics, 2010, 17(3):199-219.
[4]Kim Y, Nelson P A. Optimal regularization for acoustic source reconstruction by inverse methods[J]. Journal of Sound and Vibration , 2004, 275(4-5):463-487.
[5]Thite A N, Thompson D J. The quantification of structure-borne transmission paths by inverse methods[J]. Journal of Sound and Vibration, 2003, 264(3):411-451.
[6]Nelson P A,Yoon S H. Estimation of acoustic source strength by inverse methods[J]. Journal of Sound and Vibration, 2000, 233(4): 643-705.
[7]Choi H G,Thite A N, Thompson D J. A threshold for the use of Tikhonov regularization in inverse force determination[J]. Applied Acoustics, 2006, 67(7):700-719.
[8]Choi H G, Thite A N,Thompson D J. Comparison of methods for parameter selection in Tikhonov regularization with application to inverse force determination[J]. Journal of Sound and Vibration,2007, 304(3-5):894-917.
[9]Janssens M H A, Verheij J W. A pseudo-forces methodology to be used in characterization of structure-borne sound sources [J].Applied Acoustics, 2000, 61(3):285-308.
[10]Tikhonov A N, Arsenin V Y. Solutions of Ill-posed problems [M]. New York: Wiley, 1977.
[11]Golub G H, Heath M, Wahba G. Generalized cross-validation as a method for choosing a good ridge parameter[J]. Technometrics, 1979,21(2): 215-223.
[12]Hansen P C. Analysis of discrete ill-posed problems by means of the L-curve [J].SIAM Review, 1992, 34(4):561-580.
[13]张 方,秦远田.工程结构动载荷识别方法[M].北京:国防工业出版社,2011.
[14]王振杰.测量中不适定问题的正则化解法[M].北京:科学出版社,2006.
