基于LQR控制的平面二级倒立摆系统的研究

2014-09-04凌有铸陈孟元

荆楚理工学院学报 2014年4期

关键词：摆杆拉格朗模糊控制

陶明，凌有铸，陈孟元

(安徽工程大学安徽省电气传动与控制重点实验室，安徽芜湖 241000)

基于LQR控制的平面二级倒立摆系统的研究

陶明，凌有铸，陈孟元

(安徽工程大学安徽省电气传动与控制重点实验室，安徽芜湖 241000)

为实现平面二级倒立摆控制系统的稳定控制，研究设计了基于LQR的控制系统。通过对平面二级倒立摆实际物理结构的分析，建立了基于拉格朗日方程的动力学模型。通过试验确定加权矩阵Q，在理论上验证LQR算法的可行性。在GLPI2001倒立摆实验平台下，验证了LQR控制效果的有效性。

倒立摆；拉格朗日方程；LQR

0 引言

倒立摆控制系统具有强耦合、非线性、多变量、高阶次、结构不稳定等特点[1]。因此，倒立摆控制系统成为了各种先进控制策略验证和控制理论教学的实验平台。国内外控制领域的研究人员对倒立摆控制——这一控制领域的经典问题提出了多种控制策略，其对航空航天领域、机器人领域的发展提供了很大的帮助。文献[2]采用状态反馈极点配置方法整定PD参数来实现二级倒立摆的实时控制；文献[3]利用变结构控制的方法稳定有效的控制了二级倒立摆系统；文献[4]基于模糊控制理论实现了一级倒立摆的有效控制；文献[5]利用模糊神经网络控制方法解决了二级倒立摆的控制问题；文献[6]采用LGQ最优控制实现了二级倒立摆有效控制;北京师范大学的李洪兴教授则采用变域论自适应模糊控制理论完成了四级倒立摆系统的实时控制[7]。

线性二次型调节器(linear quadratic regulator)理论是现代控制理论中很重要的一种状态空间设计方法，它采用简单的线性反馈控制结构，能够很好兼顾动态性能、鲁棒性等性能指标，其控制简单可靠，成本低廉，在控制领域具有广阔的前景。

本文首先基于拉格朗日方程，建立平面二级倒立摆系统的数学模型；然后在MATLAB环境下实现LQR控制器设计，完成仿真实验；最后，在固高科技公司的GLPI2001倒立摆实验平台下，验证LQR控制效果的有效性。

1 平面二级倒立摆数学模型的建立

图1所示为二级倒立摆实物模型，该物理模型在理想的情况下具备以下特点：

摆杆1、摆杆2和转轴均为质量均匀的刚体；除传送带与导轨之间的摩擦力外，系统内其他部件之间的摩擦力很小，可以忽略不计；空气阻力忽略不计。

平面二级倒立摆的数学模型是在拉格朗日方程推导出的动力学方程的基础上建立而成的。在保守力学系下，拉格朗日方程式[8]表现为：

(1)

其中t为时间变量，qα为广义坐标，T为系统动能，表现为广义坐标、广义速度和时间的函数。当广义坐标和广义速度均被定义为独立变量时，通过系统动能T就可以求出所有的有关的qα动力学方程。部分倒立摆以及各个符号表示的物理意义分别如表1和表2所示。

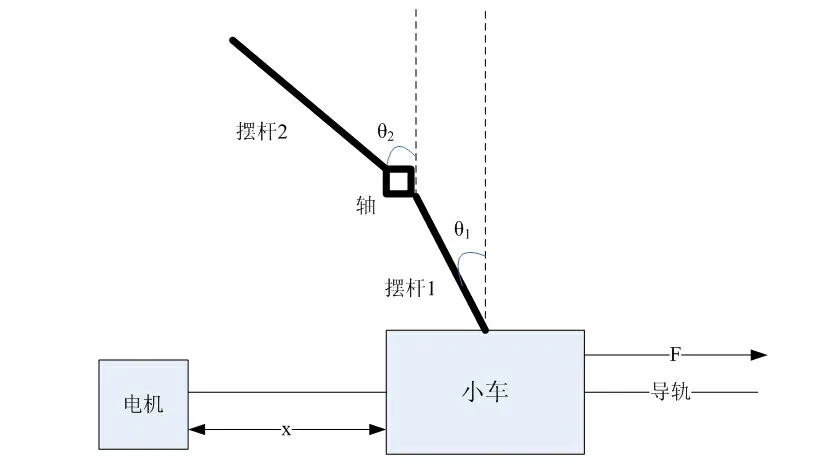
图1 二级倒立摆实物模型

表1部分倒立摆物理意义及参数值

物理意义实际数值物理意义实际数值小车质量1．096kg摆杆质量0．109kg重力加速度9．8m/s2摆杆长度0．5m摆杆质量0．00223kg

表2 各个符号表示的物理意义

在本文的二级倒立摆系统中定义了3个广义坐标，分别为x,θ1,θ2。通过拉格朗日方程式(1)得出式(2)和式(3)：

(2)

(3)

(4)

(5)

(6)

(7)

用数学方法对系统状态矩阵的能观性和能控性进行判定。系统能观能控，但是整个系统是发散的，需要设计一个控制器使得整个系统稳定。

2 LQR控制器的设计

LQR控制是线性系统中比较重要和典型的优化型问题，其特点是通过对指定性能指标函数取极大或极小而来导出系统的控制规律[9]。

LQR控制器的设计的首先步骤是假设一个状态反馈公式U=-Kx，由此形成一个稳定的闭环反馈系统。整个控制器设计的关键是确定状态反馈矩阵K。根据线性二次型最优控制理论，状态反馈矩阵K满足相对于状态和控制的二次型性能指标函数：

(8)

使得关于U的指标函数J取最小值。其中Q为x的加权矩阵，R为u的加权矩阵，且Q,R均为半正定矩阵，x是状态变量，u为输入变量。

利用MATLAB中的LQR函数能很简便的求出K矩阵，其中Q11、Q22、Q33分别代表对小车位移x、下摆角θ1、上摆角θ2的加权作用。在一般的LQR控制器中R=1，选取不同的Q矩阵值，可以得出不同的K矩阵，对各状态变量的加权有不同影响，通过多次重复的试凑得出合适的实验数据。当Qii选取较小的值时，系统的动态性能不能够满足要求；当Qii选取较大的值时系统的动态性能会有很大的改善，能够满足系统响应；当Qii选取的值过大时，系统的鲁棒性和快速性都能够得到很好的体现，但是由于控制量过大系统会有明显震荡。经过多次实验选取Q11=200，Q22=400，Q33=400，是比较合适的值，能够保证系统稳定运行。由此得到状态反馈K矩阵：[14.1421 106.3946 -181.25 15.63 3.0372 -29.3671]。

3 系统仿真与运行结果

通过MATLAB语言编程，在MATLAB环境下建立平面二级倒立摆仿真模型，将所得的状态反馈K矩阵带入至仿真模型中，设该系统的输入量为单位阶跃响应，得到各个控制量的仿真图。由图2～4可以得出：小车在4 s左右能够达到稳定运行，下摆角比上摆角的调节时间略短，小车能够很快的稳定在平衡位置，不会出现很大的偏移。