基于Mogi-Coulomb强度准则的隧道围岩理想弹塑性解答
2014-09-04吕彩忠
吕彩忠
(衢州学院 建筑工程学院,浙江 衢州 324000)
基于Mogi-Coulomb强度准则的隧道围岩理想弹塑性解答
吕彩忠
(衢州学院 建筑工程学院,浙江 衢州 324000)
合理选择岩石强度准则对隧道应力及位移预测和支护设计都具有重要意义,基于Mogi-Coulomb强度准则和理想弹塑性模型,通过中间主应力系数反映中间主应力的影响,推导了圆形隧道围岩应力和位移的解析解,并对所得结果进行比较与验证,得到了中间主应力和围岩抗剪强度参数的影响特性。研究表明:具有广泛的适用性和较好的可比性,Mohr-Coulomb强度准则解答和Matsuoka-Nakai准则解答均为其特例;结果关于中间主应力系数b=0.5对称,较好地反映了岩石强度的中间主应力效应及其区间性;粘聚力及内摩擦角对围岩塑性区半径和隧道洞壁位移的影响显著,应充分考虑中间主应力影响及围岩抗剪强度参数变化对隧道设计与施工的影响。
隧道工程;Mogi-Coulomb强度准则;理想弹塑性模型;中间主应力;应力和位移
应用能合理反映岩石力学性状的强度准则,可以充分发挥岩石材料的强度潜能,将给隧道、边坡等岩石工程建设带来巨大的经济效益。众多岩石真三轴试验已表明[1-3]:中间主应力σ2对岩石的强度具有提高作用,并且其影响具有区间性。隧道开挖施工造成的地应力重分布,使围岩处于弹塑性状态,隧道轴向应力对其横断面内的应力和变形具有重要影响,但当前对隧道围岩进行的弹塑性分析多采用Mohr-Coulomb强度准则[4-5]或Hoek-Brown强度准则[6-7],均没有考虑中间主应力σ2的影响,所得结果过于保守,致使隧道施工与设计的浪费极大;已有学者将考虑中间主应力σ2影响的统一强度理论[8-9]和Matsuoka-Nakai(又称广义空间滑动面SMP)[10-11]准则应用于围岩弹塑性分析,但所得结果表达复杂不便于工程应用。Mogi[12-13]较早开展了岩石真三轴仪的研制及多种岩石的真三轴试验研究,并提出了Mogi经验强度准则通式。Al-Ajmi等[14]将线性Mogi经验强度准则和Coulomb强度准则相结合,建立了能反映岩石中间主应力效应及其区间性影响的Mogi-Coulomb强度准则,已在井壁稳定性分析及岩石真三轴强度预测中得到了广泛应用与验证[15-18]。本文将基于Mogi-Coulomb强度准则和理想弹塑性模型,对圆形隧道围岩进行弹塑性分析,推导其应力和位移的解析解,并对所得结果进行比较与验证,最后探讨中间主应力和围岩抗剪强度参数的影响特性。
1 Mogi-Coulomb强度准则
Mogi根据自己所开展的多种岩石真三轴试验数据,提出的Mogi经验强度准则通式为[12-13]
τoct=f(σ13)
(1)

式中:σ1、σ2和σ3分别为大主应力、中间主应力和小主应力,以压应力为正;τoct为八面体剪应力;σ13为与中间主应力σ2平行的破裂面上的平均主应力;f为单调递增函数,可采用一次直线式、二次多项式或幂函数。
Al-Ajmi等[14]将线性Mogi经验强度准则和Coulomb强度准则相结合,建立了以岩石抗剪强度参数(粘聚力c和内摩擦角φ)表示的Mogi Coulomb强度准则,其表达式为
τoct=kσ13+d
(2)

由式(2)可见,Mogi-Coulomb强度准则考虑了中间主应力σ2对岩石强度的影响,且其参数(粘聚力c和内摩擦角φ)与Mohr-Coulomb强度准则相同,物理意义明确且便于由常规三轴压缩试验确定。Mogi-Coulomb强度准则的极限线为外接Mohr-Coulomb强度准则的曲边六边形[18],在轴对称的三轴压缩状态和三轴拉伸状态时二者重合,如图1所示。
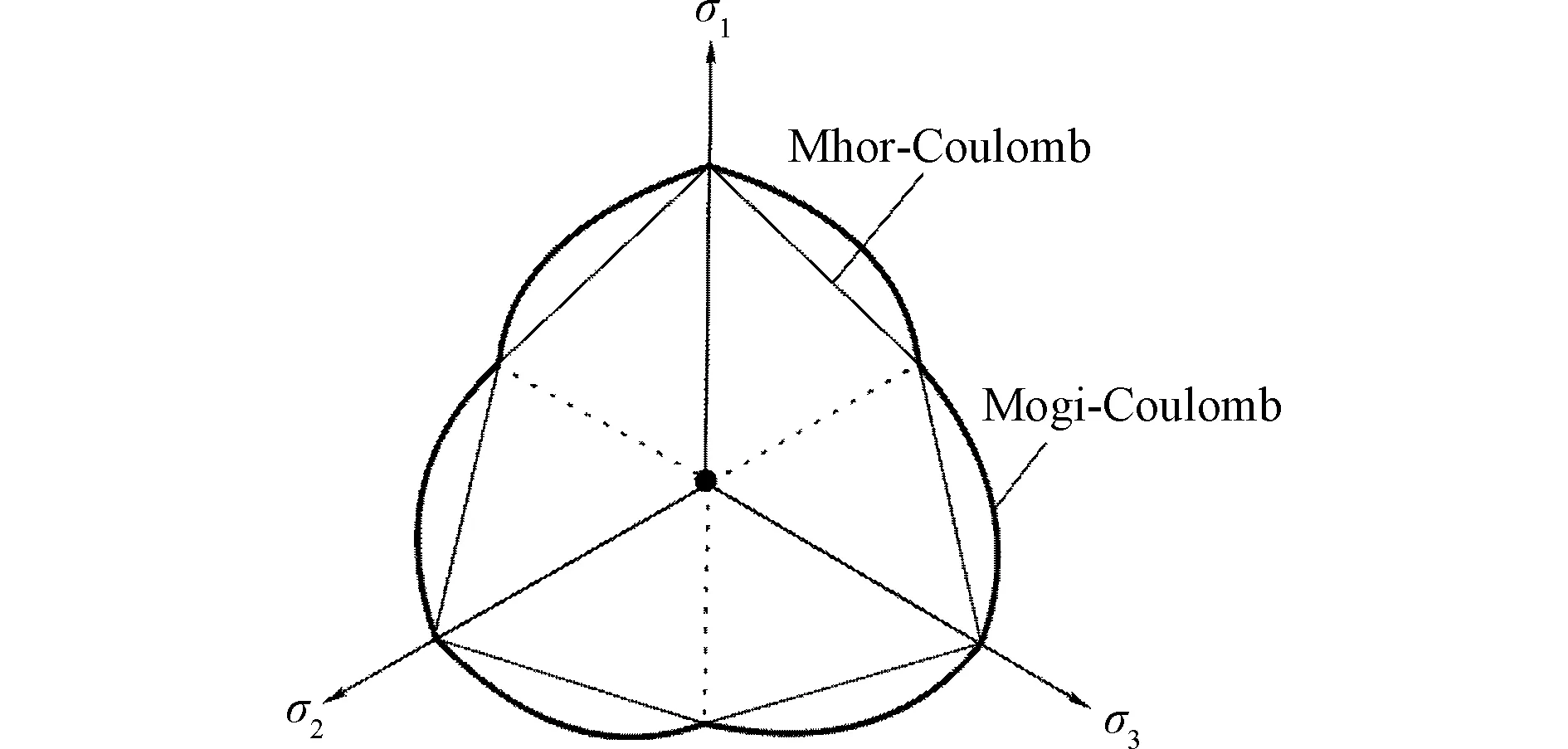
图1 Mogi-Coulomb强度准则的极限线
工程实践和真三轴试验研究中,常用中间主应力系数b来表示中间主应力σ2与大主应力σ1和小主应力σ3的相对大小关系,其表达式为

(3)
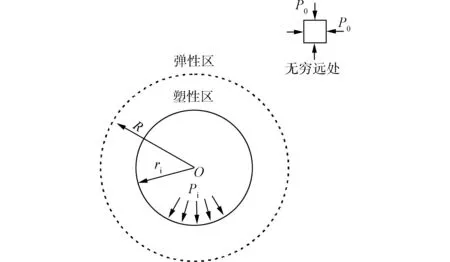
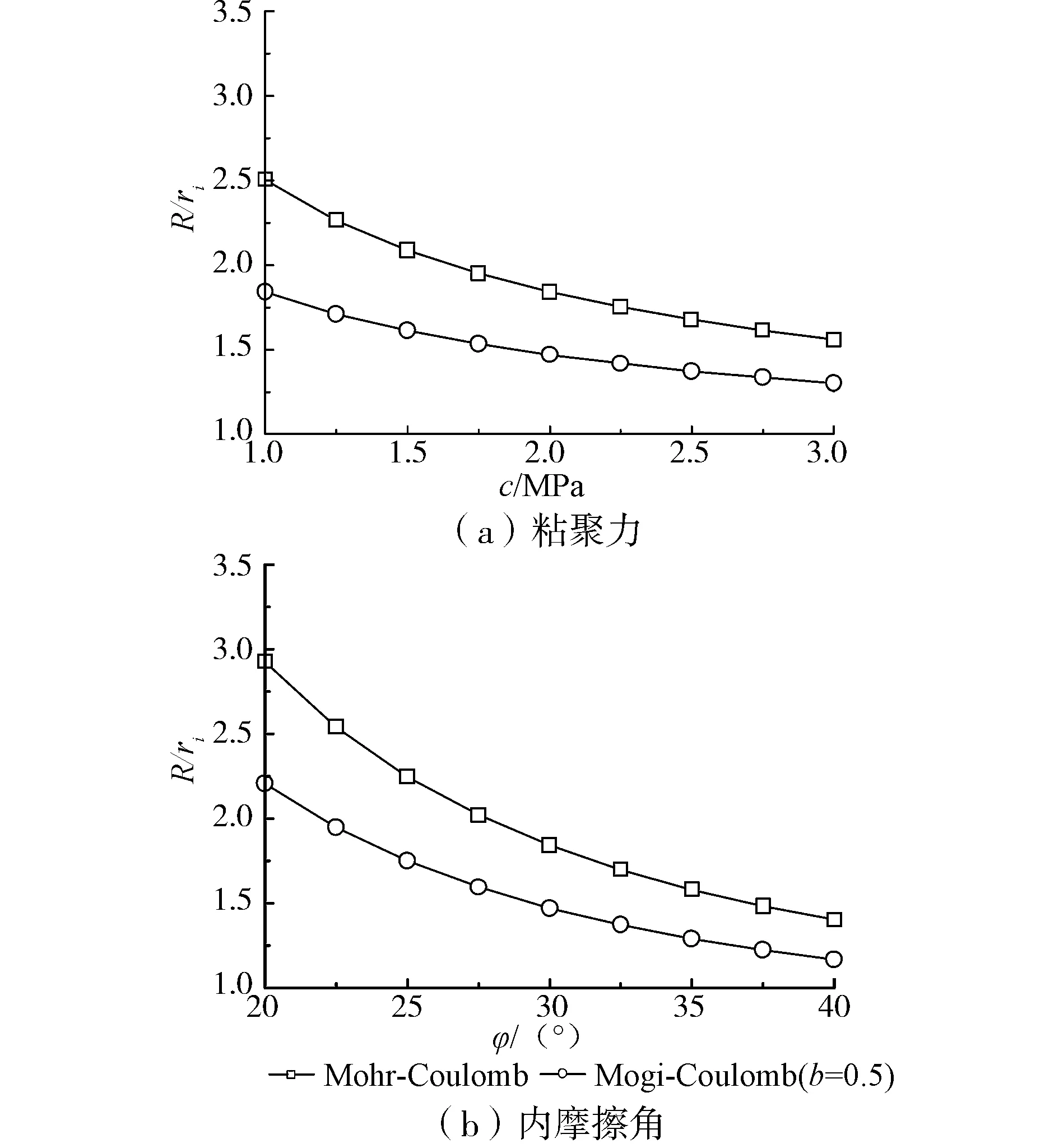
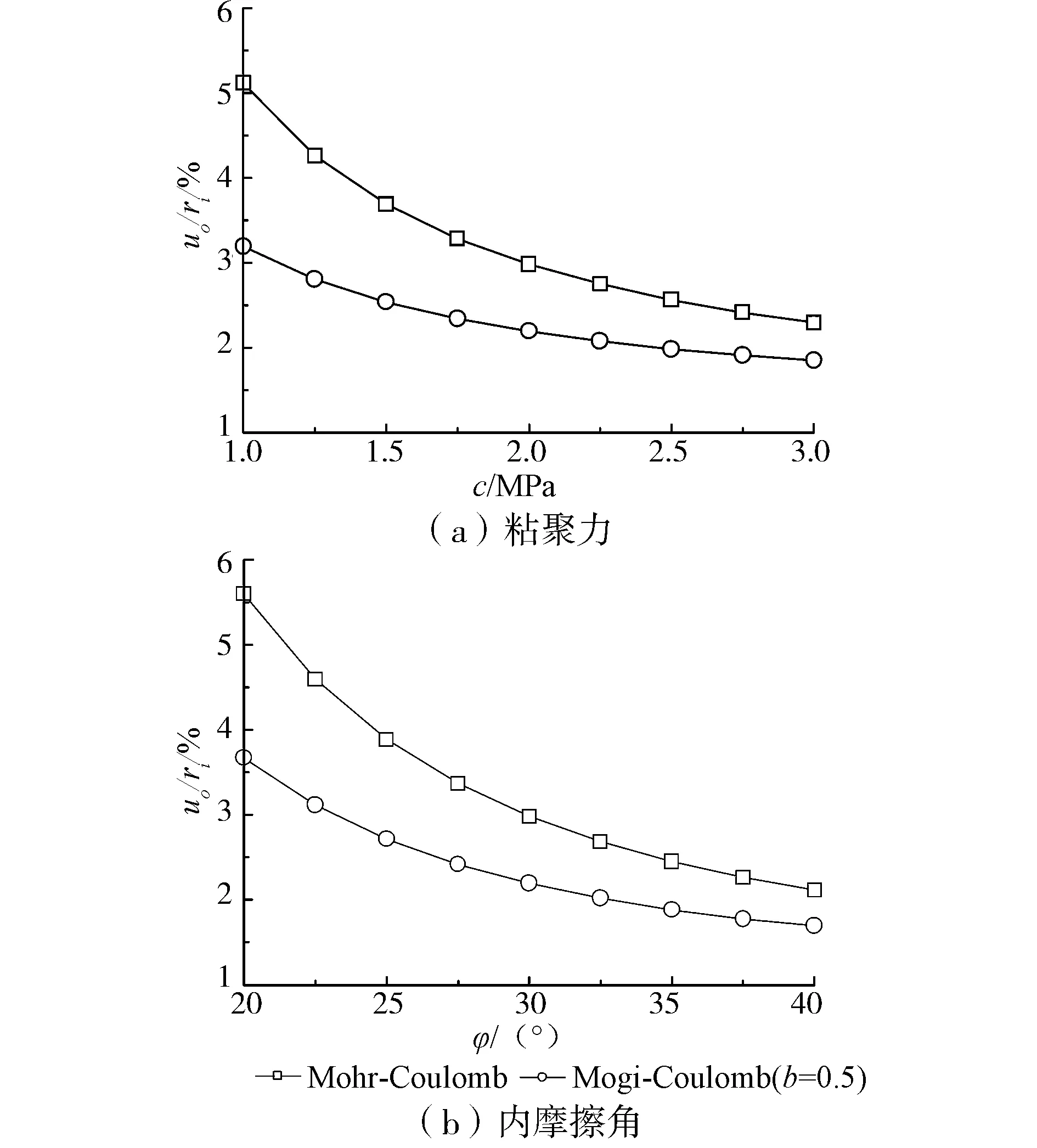
中间主应力系数b的取值范围为[0,1],系数b=0对应σ2=σ3<σ1的轴对称三轴压缩状态,系数b=1对应σ3<σ2=σ1的轴对称三轴拉伸状态,0 σ2=bσ1+(1-b)σ3 (4) 将式(4)代入式(2),整理得Mogi-Coulomb强度准则为 σ1=Aσ3+B (5) 当系数b=0或1时,Mogi-Coulomb强度准则式(5)退化为Mohr-Coulomb强度准则,即 (6) 故Mohr-Coulomb强度准则为Mogi-Coulomb强度准则的特例,对应系数b=0或1,没有考虑中间主应力σ2的影响。 假定围岩为均匀、连续、各向同性的理想弹-塑性材料,隧道轴向应力σz为中间主应力σ2。圆形隧道内表面受均匀支护力pi作用,无穷远处受等值地应力po作用,如图2所示,图中ri为隧道半径、R为围岩塑性区半径。 图2 隧道力学模型 不考虑围岩自重,轴对称条件下平衡微分方程为 (7) 在围岩塑性区内,σ1=σθ,σ3=σr,则Mogi-Coulomb强度准则式(5)变为 σθ=Aσr+B (8) 将式(8)代入式(7),并以隧道洞壁处r=ri,σr=pi为应力边界条件,求得围岩塑性区的应力为 (9) 设ps为围岩临界支护力即弹塑性交界处的径向应力,则围岩弹性区的应力和位移为[7] σr=po-(po-ps)R2/r2,σθ=po+(po-ps)R2/r2 (10) (11) 式中:E和ν分别为围岩的弹性模量与泊松比。 在弹塑性交界r=R处,围岩弹性区的应力式(10)应满足Mogi-Coulomb强度准则式(8),且r=R处的径向应力σr连续,据此求得围岩临界支护力ps和塑性区半径R分别为 (12) 当支护力pi小于临界支护力ps时,围岩才进入弹塑性状态。在围岩塑性区内,大主应变ε1=εθ,小主应变ε3=εr,不考虑围岩塑性区的体积变化,则 εv=εθ+εz+εr=0 (13) 隧道轴向应变εz=0,将εr=du/dr,εθ=u/r代入式(13),并以围岩弹塑性交界r=R处的位移为位移边界条件,求得围岩塑性区的位移为 (14) 将r=ri代入式(14),即得隧道的洞壁位移uo为 (15) 基于Mogi-Coulomb强度准则,隧道围岩塑性区和弹性区的应力可分别由式(9)和式(10)确定,塑性区和弹性区的位移则可分别由式(11)和式(14)确定。围岩位移式(11)和式(14)的表达式虽相同,但二者的应用区域不同:式(11)只适用于r>R的围岩弹性区,式(14)适用于ri 此处主要对本文结果进行比较与验证,同时探讨中间主应力和围岩抗剪强度参数的影响特性。取文献[10]中代表性的圆形软岩隧道:围岩参数为c=2.0 MPa,φ=30°,ν=0.5,E=2.0 GPa;隧道半径ri=3.0 m,初始地应力po=20 MPa,无支护隧道即支护力pi为零,围岩处于弹塑性状态。 3.1 结果比较与验证 不同强度准则所建立的依据以及对中间主应力σ2的考虑都不尽相同,因而采用不同强度准则的计算结果之间常有较大差异。将文献[4]中基于Mohr Coulomb强度准则的围岩理想弹塑性解答与本文系数b=0时的结果进行比较,如图3所示;将文献[10]中基于Matsuoka-Nakai(SMP)准则的围岩理想弹塑性解答与本文系数b=0.285时的结果进行比较,如图4所示。 由图3可以看出,本文系数b=0时的应力及塑性区位移和Mohr-Coulomb强度准则解答的峰值和分布规律均吻合的极好,二者的围岩塑性区半径R=1.84ri也完全相同。由图4可以看出,系数b=0.285时本文结果和考虑中间主应力σ2影响的Matsuoka-Nakai(SMP)准则解答吻合的也较好,且二者的围岩塑性区半径R相同并减小为1.53ri。这都说明本文基于Mogi-Coulomb强度准则所得结果的正确性和合理性,同时也说明基于Mohr-Coulomb强度准则和基于Matsuoka-Nakai(SMP)准则的围岩理想弹塑性解答都是本文结果的特例,因此本文结果具有广泛的适用性和较好的可比性。 图3 本文结果(b=0)与Mohr-Coulomb强度准则解答的比较 图4 本文结果(b=0.285)与Matsuoka-Nakai(SMP)准则解答的比较 3.2 参数分析 1)中间主应力影响 中间主应力σ2可在大主应力σ1和小主应力σ3之间变化,对应的中间主应力系数b在0和1之间变动。中间主应力σ2对岩石强度具有增强作用,但岩石强度一般是随着中间主应力σ2的增加先逐渐增大,达到峰值后又随中间主应力σ2的增加而逐渐降低,即中间主应力效应具有区间性[1-3]。图5给出了围岩塑性区半径R和隧道洞壁位移uo与系数b的变化关系,Mohr-Coulomb强度准则解答也一并标于图中。 图5 中间主应力的影响 由图5可以看出,Mohr-Coulomb强度准则解答与系数b即中间主应力σ2无关,且围岩塑性区半径R=1.84ri和隧道洞壁位移uo=0.029 8ri与本文系数b=0或1时的结果相同且最大;本文基于Mogi-Coulomb强度准则的结果关于系数b=0.5即σ2=(σ1+σ3)/2对称,且最小分别达到R=1.47ri、uo=0.021 9ri,较好地反映了岩石强度的中间主应力效应及其区间性,相比Mohr-Coulomb强度准则解答具有明显的优越性。合理考虑中间主应力效应及其区间性,可更加充分发挥围岩的强度潜能,更经济安全地进行隧道设计与施工。 2)围岩抗剪强度参数影响 围岩的抗剪强度包括粘聚力和摩擦滑移两部分,以粘聚力c和内摩擦角φ为代表的抗剪强度参数的变异性可使围岩的强度变化很大。图6和图7分别给出了系数b=0.5时,围岩塑性区半径R和隧道洞壁位移uo随粘聚力c及内摩擦角φ的变化关系,Mohr-Coulomb强度准则解答也标于图中。 由图6、7可知,Mohr-Coulomb强度准则解答均大于本文系数b=0.5时的结果,但随着粘聚力c及内摩擦角φ的增加,二者之间的差异在不断减小。围岩塑性区半径R和隧道洞壁位移uo随粘聚力c及内摩擦角φ的增加均呈非线性减小,c=3.0 MPa时塑性区半径R和洞壁位移uo分别比c=1.0 MPa时减小了29.4%、42.2%,φ=40°时二者比φ=20°时分别减小了47.1%、53.9%,可见粘聚力c及内摩擦角φ对围岩塑性区半径R和隧道洞壁位移uo的影响显著,且相比对隧道洞壁位移uo的影响更明显。 图6 围岩抗剪强度参数对塑性区半径的影响 图7 围岩抗剪强度参数对隧道洞壁位移的影响 1)依据引入中间主应力系数b的Mogi-Coulomb强度准则,推导了圆形隧道围岩应力和位移的理想弹塑性解答,并利用文献已有的Mohr-Coulomb强度准则解答和Matsuoka-Nakai(SMP)准则解答对其进行了比较与验证,同时指出这两个解答均为本文结果的特例,表明本文结果具有广泛的适用性和较好的可比性。 2)围岩塑性区半径R和隧道洞壁位移uo关于中间主应力系数b=0.5对称,较好地反映了岩石强度的中间主应力效应及其区间性,相比Mohr-Coulomb强度准则解答具有明显的优越性;粘聚力c及内摩擦角φ对围岩塑性区半径R和隧道洞壁位移uo的影响显著,且对隧道洞壁位移uo的影响更明显。 [1] 许东俊, 耿乃光. 岩石强度随中间主应力变化规律[J]. 固体力学学报, 1985, 6(1):72-80. Xu D J,Geng N G. The variation law of rock strength with increase of intermediate principal stress [J]. Acta Mechanica Solida Sinica, 1985, 6(1):72-80. [2] Haimson B C, Chang C. A new true triaxial cell for testing mechanical properties of rock, and its use to determine rock strength and deformability of westerly granite [J]. International Journal of Rock Mechanics and Mining Sciences, 2000, 37(1/2):285-296. [3] Colmenares L B, Zoback M D. A statistical evaluation of intact rock failure criteria constrained by polyaxial test data for five different rocks [J]. International Journal of rock mechanics and Mining Sciences, 2002, 39(6):695-729. [4] Jawger J C, Cook N G W. Fundamentals of Rock Mechanics [M]. London:Methuen and Co. Ltd., 1979. [5] 刘夕才, 林韵梅. 软岩扩容性对巷道围岩特征曲线的影响[J]. 煤炭学报, 1996, 21(6):596-601. Liu X C, Lin Y M. Effect of dilatancy of soft rocks on rock characteristic curves of tunnels [J]. Journal of China Coal Society, 1996, 21(6):596-601. [6] Brown E T, Bray J W, Ladanyi B, et al. Ground response curves for rock tunnels [J]. Journal of Geotechnical Engineering, ASCE, 1983, 109(1):15-39. [7] Sharan S K. Analytical solutions for stresses and displacements around a circular opening in a generalized Hoek-Brown rock [J]. International Journal of Rock Mechanics and Mining Sciences, 2008, 45(1):78-85. [8] 胡小荣, 俞茂宏. 统一强度理论及其在巷道围岩弹塑性分析中的应用[J]. 中国有色金属学报, 2002, 12(5):1021-1026. Hu X R, Yu M H. Unified strength theory and its application in elasto-plastic analysis to tunnel [J]. The Chinese Journal of Nonferrous Metals, 2002, 12(5):1021-1026. [9] 张常光, 赵均海, 张庆贺. 基于统一强度理论的深埋圆形岩石隧道收敛限制分析[J]. 岩土工程学报, 2012, 34(1):110-114. Zhang C G, Zhao J H, Zhang Q H. Convergence-confinement analysis of deep circular rock tunnels based on unified strength theory [J]. Chinese Journal of Geotechnical Engineering, 2012, 34(1):110-114. [10] 朱建明, 彭新坡, 徐金海. 基于SMP准则的衬砌隧道围岩抗力系数的计算[J]. 岩土工程学报, 2011, 33(5):700-704. Zhu J M, Peng X P, Xu J H. Determination of rock resistant coefficient in lining tunnels based on SMP failure criterion [J]. Chinese Journal of Geotechnical Engineering, 2011, 33(5):700-704. [11] 吴创周, 杨林德, 李秋实. 弹脆塑性围岩应力和位移的广义SMP准则解[J]. 工程力学, 2013, 30(8):223-228. Wu C Z, Yang L D, Li Q S. Perfect elastic-plastic-brittle-plastic solution of axisymmetric circular opening in rock mass on extended SMP criterion [J]. Engineering Mechanics, 2013, 30(8):223-228. [12] Mogi K. Effect of the intermediate principal stress on rock failure [J]. Journal of Geophysics Research,1967,72(20):5117-5131. [13] Mogi K. Effect of the triaxial stress system on the failure of dolomite and limestone [J]. Tectonophysics, 1971, 11(11):111-127. [14] Al-Ajmi A M, Zimmerman R W. Relation between the Mogi and the Coulomb failure criteria [J]. International Journal of Rock Mechanics and Mining Sciences, 2005, 42(3):431-439. [15] Al-Ajmi A M, Zimmerman R W. Stability analysis of vertical boreholes using the Mogi-Coulomb failure criterion [J]. International Journal of Rock Mechanics and Mining Sciences, 2006, 43(8):1200-1211. [16] Al-Ajmi A M, Zimmerman R W. A new well path optimization model for increased mechanical borehole stability [J]. Journal of Petroleum Science and Engineering, 2009, 69(1-2):53-62. [17] Zhang L Y, Cao P, Radha K C. Evaluation of rock strength criteria for wellbore stability analysis [J]. International Journal of Rock Mechanics and Mining Sciences, 2010, 47(8):1304-1316. [18] Benz T, Schwab R. A quantitative comparison of six rock failure criteria [J]. International Journal of Rock Mechanics and Mining Sciences, 2008, 45(7):1176-1186. (编辑 胡 玲) Elastic-PerfectlyPlasticSolutionofTunnelSurroundingRocksUsingMogi-CoulombStrengthCriterion LyuCaizhong (College of Civil Engineering and Architecture, Quzhou University, Quzhou 234000, Zhejiang P.R.China) Reasonable choice of rock strength criteria is crucial for stress and displacement prediction and support design in tunnel engineering. Based on Mogi-Coulomb strength criterion and elastic-perfectly plastic model, analytical solutions of stress and displacement for surrounding rocks around a circular tunnel were derived The intermediate principal stress coefficient was used to present the intermediate principal stress effect. The results in this study were compared with the current solutions in the literatures and the influence of intermediate principal stress and shear strength parameters of surrounding rocks was discussed. The results showed extensive applicability and the Mohr-Coulomb strength criterion and Matsuoka-Nakai criterion are two special cases; when the intermediate principal stress coefficient b was equals to 0.5, the results indicated that the intermediate principal stress effect and its range for rock strength; the influence of cohesion and internal friction angle on the plastic radius and tunnel wall displacement was significant; Care should be taken to the effects of intermediate principal stress and shear strength parameter variations of surrounding rocks on tunnel design and construction. tunnel engineering; Mogi-Coulomb strength criterion; elastic-perfectly plastic model; intermediate principal stress; stress and displacement 10.11835/j.issn.1674-4764.2014.06.009 2014-04-18 浙江省自然科学基金资助项目(Y1100210) 吕彩忠(1964-),男,副教授,主要从事土木工程设计与监测研究,(E-mail)lvcz1964@163.com。 TU452 A 1674-4764(2014)06-0054-06
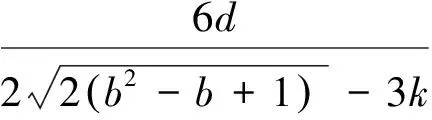

2 围岩理想弹塑性解答
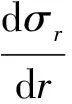
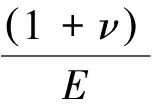

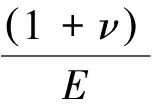
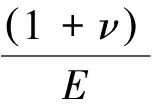
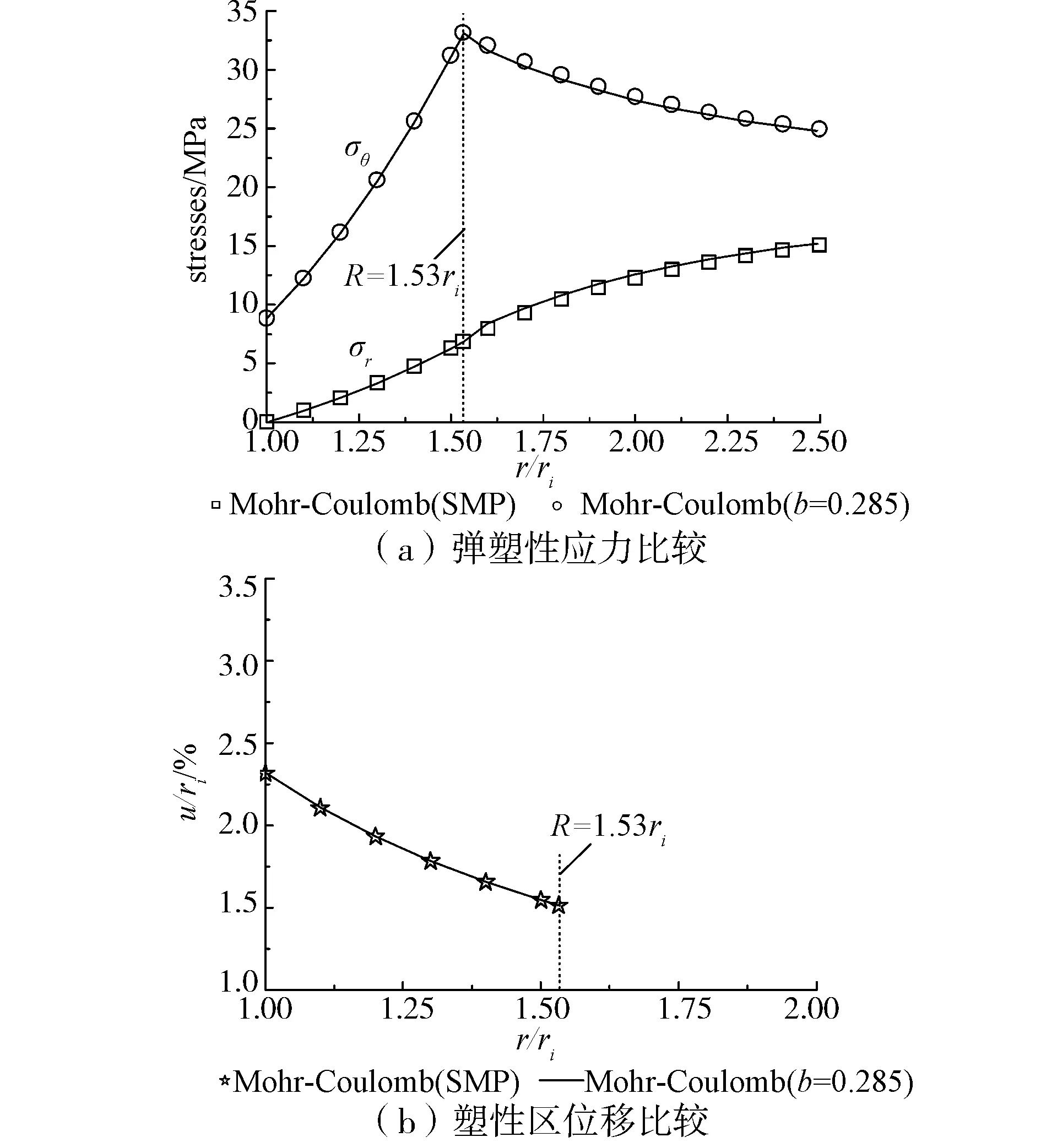
3 结果比较及参数分析


4 结论
