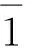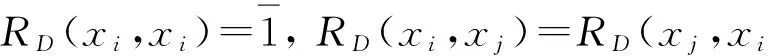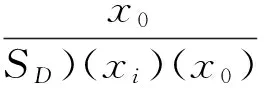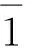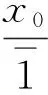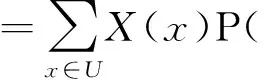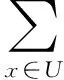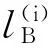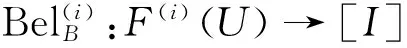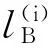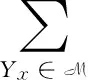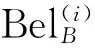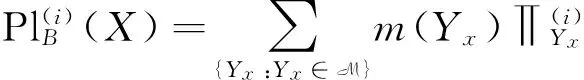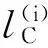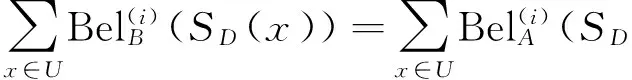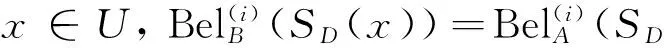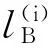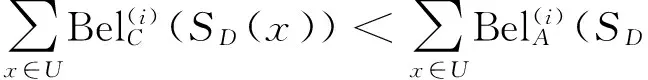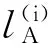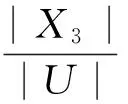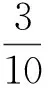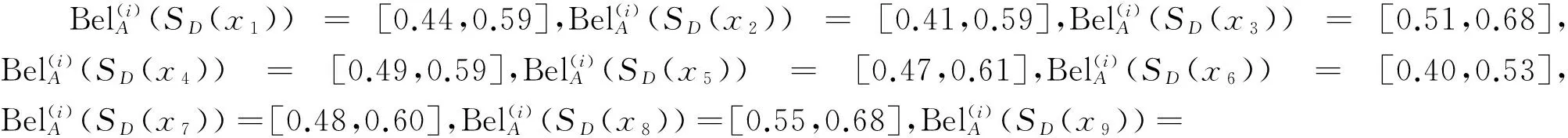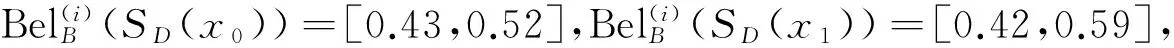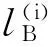IVFD信息系统的属性约简的一个注记
2014-09-01喻光继
喻光继
(广西财经学院信息与统计学院, 中国 南宁 530003)
IVFD信息系统的属性约简的一个注记
喻光继*
(广西财经学院信息与统计学院, 中国 南宁 530003)
利用粗糙集理论和推广的D-S 证据理论获得了IVFD信息系统的信任约简和似然约简.
IVF; IVFD; 信息系统;RD; 信任约简; 似然约简
粗糙集理论[1-2]和D-S 证据理论[3]都是处理不确定性问题的数学工具, 它们之间有密切关糸. 近似空间对应信任结构, 而信任函数和似然函数由信任结构产生, 从而基于近似空间的下近似算子和上近似算子对应信任函数和似然函数[4-6]. 因此, D-S 证据理论可用于研究信息系统中的属性约简问题[7-9]. 考虑到信息系统的属性值可能是语言或映射(例如IVF集), 运用粗糙集理论处理时, 会把这样的值近似地按数字或符号来处理, 而忽略一些重要信息如“偏序”、“隶属度”, 这意味着仅运用粗糙集理论不能有效地处理这类不确定性问题. 本文推广了D-S 证据理论, 运用粗糙集理论和推广的D-S 证据理论处理IVFD 信息系统的属性约简问题.
1 基本概念
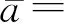
1.1 IVF集
定义1[10]∀a,b∈[I], 定义
(1)a=b⟺a-=b-,a+=b+.
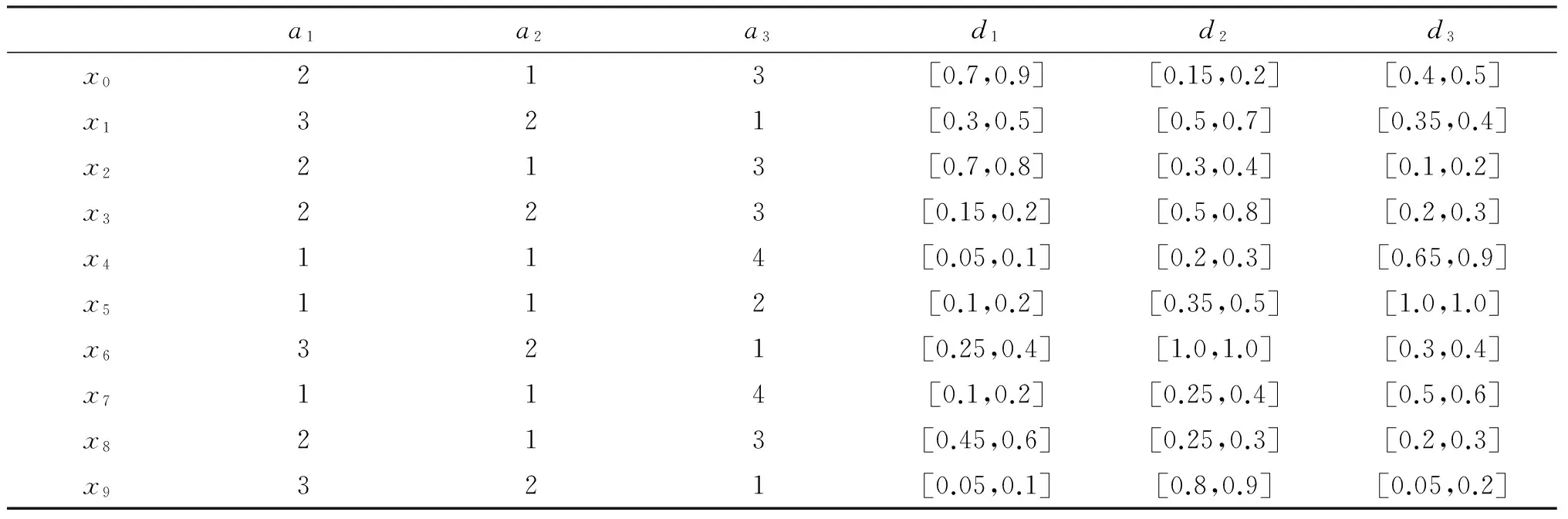
(2)a≤b⟺a-≤b-,a+≤b+;a (3)ac=[1-a+,1-a-]. 定义2[10-11]∀{ai:i∈J}⊆[I], 定义 类似于模糊集, IVF集有相应运算及运算律, 这里省略. 1.2 IVFD 信息系统 定义3[12]称(U,A∪D) 为IVFD信息系统, 其中A是条件属性集,D={dk∈F(i)(U):k=(1,2,…,r)}是决策属性集. 记D(xi)=Di1/d1+Di2/d2+…+Dir/dr(Dik∈[I],i=0,1,…,n-1,k=1,2,…,r). 例1[12]表1给出了IVFD信息系统, 其中U={x0,x1,x2,x3,x5,x6,x7,x8,x9},A={a1,a2,a3},D={d1,d2,d3}. 表1 IVFD信息系统(U,A∪D) 以i=0为例, 我们有 定义4[13]设(U,A∪D)是IVFD信息系统, 则B⊆A决定如下等价关系: RB={(x,y)∈U×U:a(x)=a(y)(∀a∈B)}. 且U/RB={[x]B:x∈U}形成了U的一个划分, 其中[x]B={y∈U:(x,y)∈RB}表示基于B由x决定的等价类. 性质1设(U,A∪D)是IVFD信息系统,若C⊆B⊆A,则∀X∈F(i)(U), 2.1 必然性IVF测度和可能性IVF测度 Zadeh[14]在模糊集基础上建立了可能性理论, Dubois等[15]发展了该理论. 现在, 我们把该理论中的必然性测度和可能性测度分别推广为必然性IVF测度和可能性IVF测度. 定义5[16]设A∈2U, 对∀X∈F(U),记 命题1设A∈2U, 对∀X∈F(i)(U),记 证不难证明, 故省略. 2.2 IVF信任函数和IVF似然函数 在文献[5] 中, 通过把焦元改为模糊集, 可将信任函数和似然函数模糊化. 现在, 我们把它们直觉模糊化, 从而推广了D-S证据理论. 类似于经典的信任函数和似然函数, 可证Bel(i)是IVF信任函数当且仅当它满足如下条件: 3.1IVF关系RD 定义7设S=(U,A∪D)是IVFD信息系统, 其中U={x0,x1,…,xn},D={d1,d2,…,xr}. 对IVFD集D,U上的IVF关系RD定义如下: SD(x)(y)=RD(x,y) (y∈U). 记 U/RD={SD(x):x∈U}. 例2在例1中, 于是 类似可算出SD(xi) (i=1,2,3,4,5,6,7,8,9),记它们在表2中. 表2 SD(xi)(xj )(i,j=0,1,2,3,4,5,6,7,8,9) 3.2 信任约简和似然约简 定义X∈F(i)(U) 的概率P(i)(X)为 其中P({x})=1/|U|. 命题3设(U,A∪D) 是IVFD信息系统,B⊆A, 对X∈F(i)(U), 记 取M=U/RB={Yx:x∈U}, 令概率分布mB为 证因为 (*) 性质2设(U,A∪D) 是IVFD信息系统, 如果C⊆B⊆A, 且X∈F(i)(U), 那么 证由性质1可推得. 定义8设S=(U,A∪D) 是IVFD信息系统,B⊆A, 引理1设S=(U,A∪D)是IVFD信息系统, 则 (2) 证明类似于(1). 定理1设S=(U,A∪D)是IVFD信息系统, 则 证(1) “⟹” 设B为S的信任约简, 则B为S的信任协调集. 由引理1(1), 由定义8(1),∀CB,∀(x)). 所以B为S的信任约简. (2) 证明类似于(1). 例3我们考虑例2. (1) 由命题1和(*),有 [0.43,0.53]. 由(1)和(2)可得B不是S的信任协调集, 从而B不是S的信任约简. [1] PAWLAK Z. Rough sets: theoretical aspects of reasoning about data [M]. Boston: Kluwer Academic Publishers, 1991. [2] 张文修, 吴伟志, 梁吉业, 等. 粗糙集理论与方法[M]. 北京:中国科技出版社, 2001. [3] SHAFER G. A mathematical theory of evidence [M]. Princeton: Princeton University Press, 1976. [4] WU W, LEUNG Y, MI J. On generalized fuzzy belief functions in infinite spaces [J]. IEEE Trans Fuzzy Syst, 2009,17(2):385-397. [5] WU W, LEUNG Y, ZHANG W. Connections between rough set theory and Dempster-Shafer theory of evidence [J]. Int J General Syst, 2002,31(4):405-430. [6] YAO Y Y. Interpretations of belief functions in the theory of rough sets [J]. Inf Sci,1998,104(1):81-106. [7] WU W. Attribute reduction based on evidence theory in incomplete decision systems [J]. Inf Sci, 2008,178(12):1355-1371. [8] WU W, ZHANG M, LI H,etal. Knowledge reduction in random information systems via Dempster-Shafer theory of evidence [J]. Inf Sci, 2005,174(3-4):143-164. [9] ZHANG M, XU L, ZHANG W,etal. A rough set approach to knowledge reduction based on inclusion degree and evidence reasoning theory [J]. Expert Syst Appl, 2003, 20(4):298-304. [10] CHENG Y, MIAO D. Rule extraction based on granulation order in information system [J]. Expert Syst Appl, 2011,38(5):12249-12261. [11] 喻光继. 关于IVF近似空间的拓扑结构[J]. 湖南师范大学自然科学学报, 2013,36(6):21-25. [12] SUN B, GONG Z, CHEN D. Fuzzy rough set theory for the interval-valued fuzzy information systems [J]. Inf Sci, 2008,178(6):2794-2815. [13] 高宁华. 区间值模糊决策信息系统的属性约简及其相关问题[M]. 南宁: 广西民族大学, 2013. [14] ZADEH L A. Probability measures of fuzzy events [J]. J Math Anal Appl, 1968,23(4):421-427. [15] DUBOIS D, PRADE H. Possibility theory [M]. New York: Plenum Press, 1988. [16] 张文修, 梁 怡, 吴伟志. 信息系统与知识发现[M]. 北京:中国科学出版社, 2003. (编辑 陈笑梅) A Note on Attribute Reduction in IVFD Information Systems YUGuang-ji* (School of Information and Statistics, Guangxi University of Finance and Economics, Nanning 530003, China) Belief reductions and plausibility reductions in IVFD information systems were obtained by using rough set theory and the generalized D-S theory of evidence. IVF; IVFD; information system;RD; belief reduction; plausibility reduction 2013-11-08 广西自然科学基金重点资助项目(2012GXNSFDA276040) * ,E-mail:guangjiyu100@126.com TP18 A 1000-2537(2014)04-0066-06
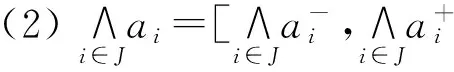

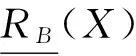
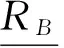
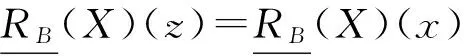
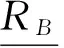
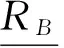
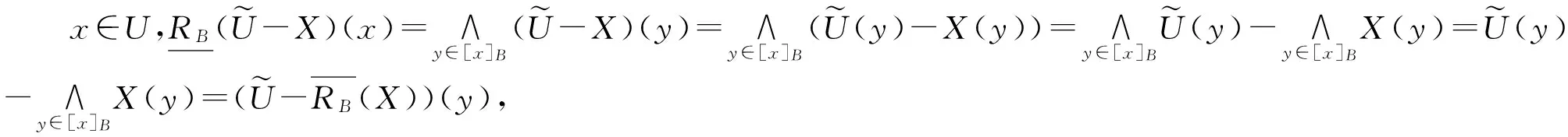
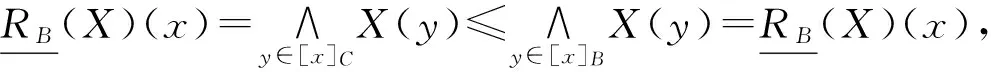
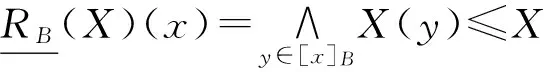

2 D-S 证据理论的推广

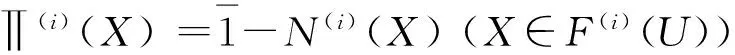
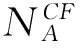
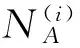

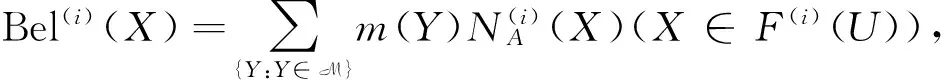
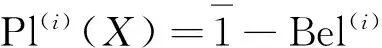
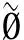
3 IVFD 信息系统中的属性约简