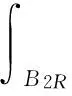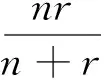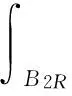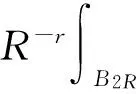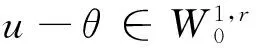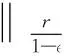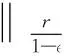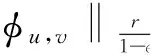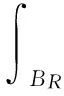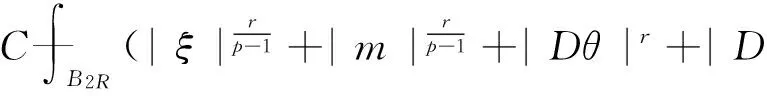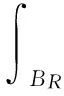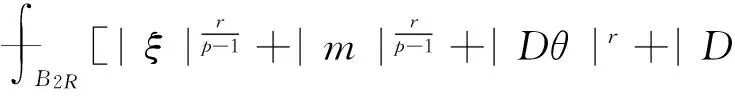一类双障碍问题的很弱解的全局正则性
2014-09-01周树清
周树清
(湖南师范大学数学与计算机科学学院,中国 长沙 410081;高性能计算与随机信息处理省部共建教育部重点实验室,中国 长沙 410081)
一类双障碍问题的很弱解的全局正则性
周树清*
(湖南师范大学数学与计算机科学学院,中国 长沙 410081;高性能计算与随机信息处理省部共建教育部重点实验室,中国 长沙 410081)
应用Hodge分解定理,得到了非齐次A-调和方程-divA(x,Du(x))=f(x,u(x))对应控制的双障碍问题的很弱解W1,q(Ω)-正则性,其中,A(x,Du(x)),f(x,u(x))满足文中所给的条件,从而推广了相关文献中的有关结果.该结果在优化控制问题中有着广泛的应用.
非齐次A-调和方程;双障碍问题;优化控制;Hodge分解;W1,q(Ω)-正则性
1 主要结果及预备引理
设1 -divA(x,Du(x))=f(x,u(x)) (1) 对应的双障碍问题,其中,A(x,h)和f(x,u)为Caratheodory函数,满足:存在正常数γ,α,β,a,使得对a.e.x∈Ω和所有的h∈Rn,有 (i)椭圆性条件 〈A(x,h),h〉≥α|h|p,h∈Rn{0}; (2) (ii)控制增长条件 |A(x,h)|≤β|h|p-1+ξ(x),|f(x,u)|≤a|u|(p-1)γ+m(x), (3) 这里,ξ(x),m(x)为Ω上给定的函数. 称区域Ω是正则的,是指使Hodge分解定理[1]都成立的区域.如Lipschitz区域是正则的. |D(v-u)|r-pD(v-u)=Dφu,v+H. (4) 受文献[2]的启发,引入如下的定义. (5) 注1“很弱”的意思是指解空间的Sobolev指数r比算子的椭圆指数p小.由Hodge分解的唯一性知,当r=p时,此定义与通常的双障碍问题的弱解的定义相同[3]. 对方程(1)的双障碍问题,有如下的正则性结果: 为了讨论双障碍问题的很弱解的全局正则性,需要对区域的边界∂Ω做一些正则性假设. (6) 在上述定义中把方体改为球体,则称边界∂Ω是pB-Poincaré厚的. 注2易证上述两种边界正则性条件是等价的. 称区域Ω是A-型区域是指:对∀x0∈Ω,0<ρ 注3由文献[5]知,Lipschitz型区域是A型区域. 先给出一些记号和引理.设0 这里,uR其中C只依赖于p,q和n. 下面的引理是Sobleve-Poincaré不等式、Hölder不等式及引理1的简单推论. 引理3[1](Hodge分解定理) 设Ω是正则的,N为正整数,0< |Du|Du=Dφ+H, (7) 并且 (8) 其中C是一个只依赖于N,n与Ω的常数. 注4由(7)及(8)易知,Dφ也有类似于(11)的估计式. 引理4[16]假定X和Y是内积空间中的向量,0≤<1,则有 ||X|X-|Y|Y|≤|X-Y|. 引理5[1,5](逆Hölder不等式) 假设f(x)和g(x)为Q⊂Rn上非负可测函数,并且满足: 其中Md(x)(g)(x)是g(x)的局部极大函数,b>1且0≤θ<1,而Q是Rn中的一个紧的方形,则存在一个常数0=0(b,n,p,θ),使得∀q∈[p,p+0),有(Q). 约定仅依赖于n,p,α,β,γ,s,a,A及R0的常数都将用同一个字母C表示. Dφu,v+H=|D(v-u)|D(v-u)=-|D{ηp[w-(u-u2R)]}|D{ηp[w-(u-u2R)]}, (9) 并且 (10) 其中C是一个只依赖于n与Ω的常数.由w的定义易得 (11) 由Minkowski不等式、引理1、式(11)及不等式(a+b)p≤ap+bp(a≥0,b≥0,0≤p≤1) (12) 于是由(10)、(12)得到 (13) (14) 把φu,v代入(5)中,并利用条件(2),(3)、引理4、Hodge分解(9)、(11)~(14)、Hölder不等式、Young不等式、Sobolev-Poincaré不等式以及Minkowski不等式,对任意V>0,有 |D{ηp[w-(u-u2R)]}D{ηp[w-(u-u2R)]}〉dx (15) (16) (17) 由(13)~(17)得 (18) |Dψ|r]dx+(C+υ+φ(R))—(|Du|t+|udx. (19) 取υ,R1,1>0足够小,即存在r1=p-1 (20) |D(v-u)|D(v-u)=Dφu,v+H=-|D[ηp(u-θ)]||D[ηp(u-θ)]|. (21) (22) 其中C是一个只依赖于n与Ω的常数. 连续零延拓函数u-θ到RnΩ,并考虑到区域是A型的,从而由引理2以及的选择可得,∂Ω是pB-Poincaré厚的.由Minkowski不等式、η的选取以及∂Ω是pB-Poincaré厚的,可得 于是 (23) (24) 把φu,v代入(5)中,并利用条件(2)、(3)、引理4、Hodge分解(22)得 (25) 由(23)、(24)、(16)、Hölder不等式及Minkowski不等式得, (26) (27) 由(25)~(27)以及(16)得 (28) 这里,τ=C(+τ1+Rφ(R)),max{1,}≤t (29) 取τ1,R0,0>0足够小,即存在r1=p-0 (30) 这里t [1] SERRIN J. Pathological solutions of elliptic differential equations[J]. Ann Sc Norm Sup Pisa, 1964,18(3):385-387. [2] LI J, Gao H. Local regularity results for very weak solutions of obstacle problems[J]. Radovi Matematiki, 2003,12:19-26. [3] LI G, MARTIO O. Stability and higher integrability of derivatives of solutions in double obstacle problems[J]. J Math Anal Appl, 2002,272(1):19-29. [4] LI G, MARTIO O. Local and global integrability of gradients in obstacle problems[J]. Ann Acad Sci Fenn Ser A I Math, 1994,19:25-34. [5] GIAQUINTQ M. Multiple integrals in the calculus of variations and nonlinear elliptic systems[M]. New Jersey: Princeton University Press, 1983. [6] CAFFARELLIL L A. The obstacle problem revisited[J]. J Fourier Ana and Appl, 1998,5(4):383-402. [7] CAFFARELLIL L A, SALSA S, SILVESTRE L. Regularity estimates for the solution and the free boundary of the obstacle problem for the fractional Laplacian[J]. Invent Math, 2008,171(2):425-461. [8] IWANIEC T, SBORDONE C. Weak minima of variational integrals[J]. J Reine Angew Math, 1994,1994(454):143-161. [9] LEWIS L. On very weak solutions of certain elliptic systems[J]. Comm Part Di Equ, 1993,18(9&10):1515-1537. [10] 高红亚,何 茜,牛红玲,等.A-调和方程障碍问题很弱解的局部正则性[J].数学物理学报,2009,29A(5):1291-1297. [11] HU H, ZHOU S, OUYANG W. Local regularity in obstacle problem[J]. J Xiangnan Univ, 2007,28(5):13-17. [12] 郑神州.拟正则映照的一些问题[D].上海:复旦大学博士论文, 1997. [13] ZHOU S, GAO H, ZHU H. Uniqueness of very weak solutions to a class of nonlinear elliptic equations[J]. Chinese J Contem Math, 2007,28(1):99-108. [14] 周树清.一类非齐次A-调和方程组很弱解的正则性[J].数学年刊, 2002,23A(3):283-288. [15] 周树清,文海英,方华强.一类非齐次A-调和方程组很弱解的性质[J].数学物理学报, 2003,23A(2):135-144. [16] IWANIEC T, MILGLIACCIO L, SBORDONE C. Integrability and removability results for quasi-regular mappings in high dimension[J]. Math Scand, 1994,75:263-279. (编辑 沈小玲) Global Regularity for very Weak Solutions to a Class of Double Obstacle Problems ZHOUShu-qing* (School of Mathematics and Computer, Hunan Normal University, Changsha 410081, China;Key Laboratory of High Performance Computing and Stochastic Information Processing, Changsha 410081, China) Using Hodge decomposition theorem,W1,q(Ω) -regularity for very weak solutions to double obstacle problems associated with non-homogeneousA-harmonic equations div(A(x,Du(x)))=f(x,u(x)) is obtained under certain conditions onA(x,Du(x)),f(x,u(x)) listed in the context, and therefore the corresponding results in related literatures are generalized. The results could be widely used in optimal control problems. non-homogeneousA-harmonic equation; double obstacle problems; optimal control; Hodge decomposition;W1,q-regularity 2013-04-27 国家自然科学基金资助项目(10971061、11271120);湖南省自然科学基金资助项目(11JJ6005);湖南省重点学科建设资助项目 * ,E-mail:zhoushuqing@163.com O175.25 A 1000-2537(2014)04-0072-05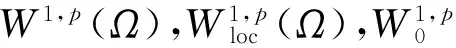
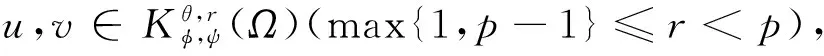
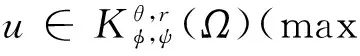

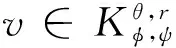
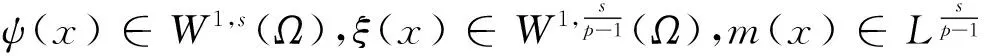
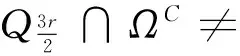
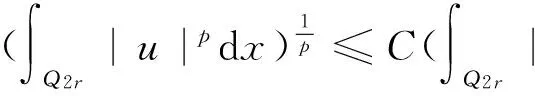
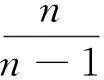

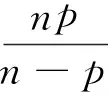
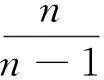
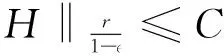
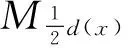
2 定理1及定理2的证明