应用Bernoulli型简单方程求(2+1)维KP方程的精确行波解

和玲超 ，庞 晶，赵忠龙

(1.内蒙古工业大学理学院，中国 呼和浩特 010051;2.中国矿业大学理学院，中国 徐州 221116)

应用Bernoulli型简单方程求(2+1)维KP方程的精确行波解

和玲超1，庞 晶1*，赵忠龙2

(1.内蒙古工业大学理学院，中国 呼和浩特 010051;2.中国矿业大学理学院，中国 徐州 221116)

利用行波变换把(2+1)维KP方程化成常微分方程，再运用简单方程法求解(2+1)维KP方程的行波解. 文中选取 Bernoulli方程为简单方程.将由KP方程所化成的常微分方程分成两部分：一部分包含导数项，另一部分为方程其他部分. 然后, 平衡最高次幂的非线性项所产生的最高次数和最高阶导数项所产生的最高项的次数，得到平衡方程，确定解的形式. 最后解得(2+1)维KP方程的行波解.

简单方程法；(2+1)维KP方程；精确行波解

在过去的30年里, 非线性偏微分方程数学模型广泛应用于自然现象和社会现象中. 比如流体力学和湍流理论, 神经学，混沌理论和生态学，孤子理论，生物学，动力系统理论等. 模型中的偏微分方程的精确解在以下几方面有着重要的用途. 首先这些解描述了不同类型的波. 在研究海底暗流，石油钻探和海洋开发等方面有广泛的应用. 其次，在所研究的系统中，特解可以作为程序模拟过程中计算机的初始条件，为计算机软件的开发提供理论支撑. 求解偏微分方程精确解中著名的方法有反散射变换和Hirota方法[1]. 在多年研究课题中，许多获得非线性偏微分方程精确解的方法已经得到了发展. 通过这些方法，许多方程的精确解已经获得. 比如Kuramoto-Sivasinsky方程[2]， sine-Gordon 方程[3-5]，Korteweg-de Vries方程[6],种群动态模型方程，Poisson-Boltzmann方程[7]等.而获得非线性偏微分方程的精确解和近似解的一个直接的方法是简单方程方法[8-12]. 该方法或修正的简单方程方法已应用于许多非线性偏微分方程，如Fisher方程，反应类扩散和反应的电报方程[13]，广义Kuramoto-Sivasinsky方程[14]，广义Swift-Hohenberg方程和广义Rayleigh方程[15]．在本文中，作者将运用简单方程方法得到(2+1)维Kadomtsev-Petviashvili方程的精确行波解.

1 方法的引入

1.1 用简单方程法研究非线性偏微分方程.

假设一个偏微分方程经过行波变换化成如下形式的常微分方程：

(1)

这个方程的精确解可以构造成如下级数形式.

(2)

其中G(ξ)是一些常微分方程也就是所说的简单方程的解，所选取的简单方程应具有下面两条性质：

(ⅰ)简单方程的阶数比方程(1)的阶数低;

(ⅱ)知道简单方程的一般解或者至少知道简单方程的一个特殊的解.

本文中，选Bernoulli方程作为简单方程，它拥有的精确解可由初等函数构造得到.所选的Bernoulli方程形式如下：

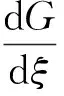
(3)

其中k是整数，k>1,有如下形式的解：

这里c,d为常数，C为积分常数.

1.2 平衡方程法

下面寻找方程(1)具有(2)形式的解.把(2),(3)代入(1)得到如下形式的多项式方程：

H=κrGr+κr-1Gr-1+…+κ0=0,

(4)

其中r为整数，当方程(4)的系数全为0时，求解得到的对应代数方程组，可以得到方程(1)的解, 其中κl是关于A0,A1,…,AM,c,d, 和方程(1)系数的多项式.

令κl=0,l=r,r-1,…,0,得到一个非线性代数系统. 为了确保得到的代数方程组中的每个方程至少有两项, 必须平衡多项式方程(4)的最高次幂.事实上，容易观察到只要平衡(1) 最高次幂的非线性项所产生的最高次数和(1)中最高阶导数项所产生的最高项的次数即可．

若方程(1)的具体形式为

(5)

则简单方程为Bernoulli方程时，平衡方程为：

ZM=M+N(k-1).

2 应用Bernoulli型简单方程求(2+1)维KP方程的精确行波解

Kadomtsev-Petviashvili方程(简称KP方程)：

(6)

其中α,γ,ε均为自由参数.方程(6)可看作KdV方程在高维情形下的推广，它用于描述水波的运动，最早由Kadomtsev和Petviashvili提出.

假设KP方程的行波解为：u(x,y,t)=ψ(ξ),ξ=x-st+wy，其中s为波速，w为y方向上的波数.

方程(7)经过行波变换后，关于ξ积分两次得

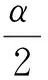
(7)

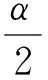
B1ψ″+B2ψ+B3ψ2=0.

(8)

考虑方程(7)具有如下形式的解：

其中G(ξ)满足Bernoulli方程,M是正整数，M可由1.2节中的平衡程序得到.

M+2(k-1)=2M,

当k=2时，M=2.

因此解的形式如下：

ψ(ξ)=A0+A1G+A2G2,G=G(ξ).

(9)

把(9)式带入方程(8)使所有有关Gi的项的系数为0，即可得到一个关于A0，A1和A2代数方程系统，这些代数方程为：

A1B1c2+A1B2+2A0A1B3=0,

2A1B1d2+10A2B1cd+2A1A2B3=0,

(10)

其中B1,B2和B3是方程(8)中的系数，解代数方程(10)，得

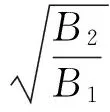
当c>0和d<0时，方程(8)的解为

当c<0和d>0时，方程(8)的解为

C为积分常数.

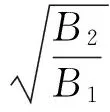
(11)

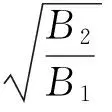
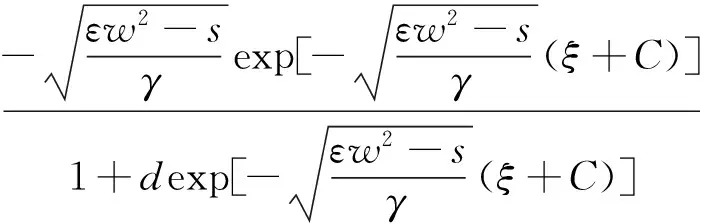
(12)

利用Mathematica软件，绘出自由参数α=1,γ=1,ε=1时解(11)的ξ-u平面上的行波图，见图1.

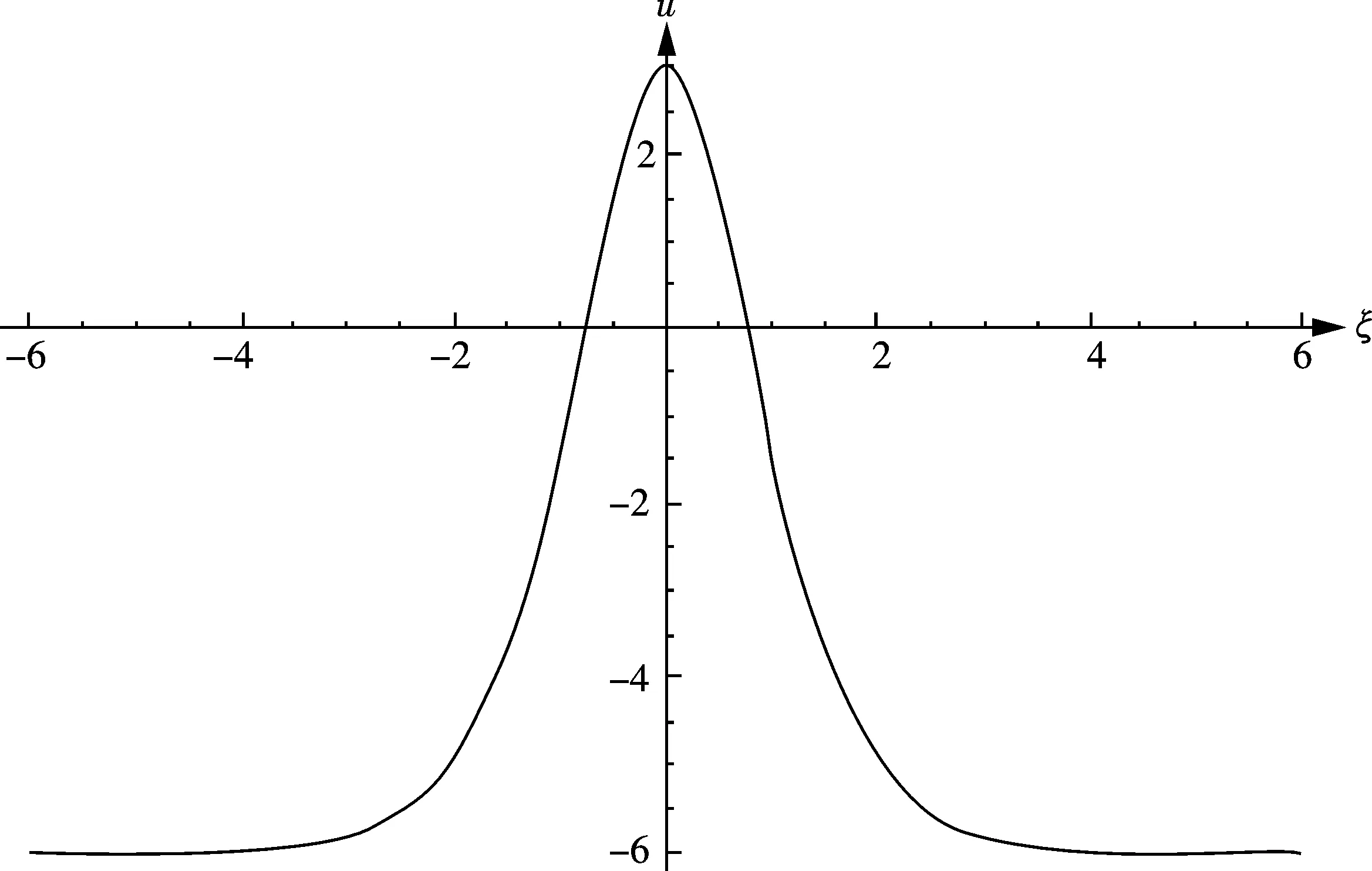
图1 解(11)的孤波图Fig.1 Profile of solution (11)

从图1可见，解(11)的图像是光滑可微的，ξ→±∞时，u→-6，可见方程的行波解是局部化的孤立波解，此时孤子解的波形为钟状.

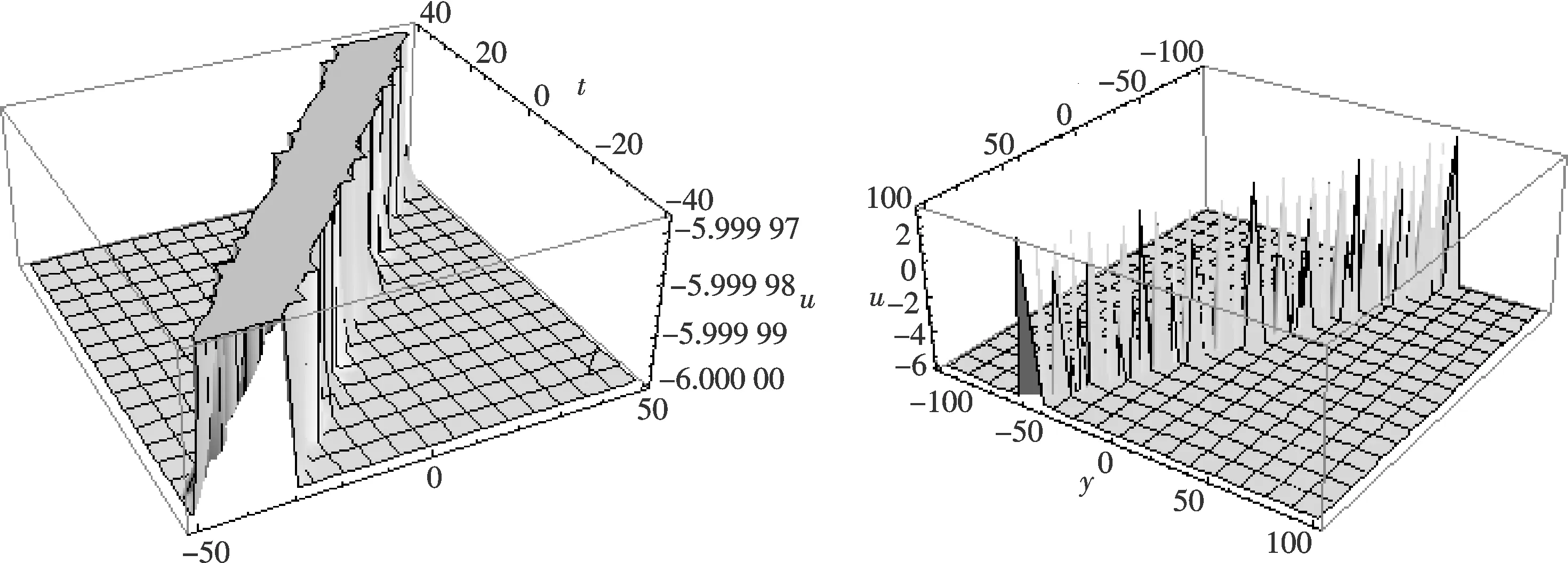
图2 解(11)的孤波图 图3 解(11)的孤波图Fig.2 Profile of solution (11) Fig.3 Profile of solution (11)

注平衡方程ZM=M+N(k-1)中,Z是方程(5)中非线性项的最高次数，M是多项式(2)式的最高次幂的次数，k是所选Bernoulli方程中的参数.

3 结束语

近年来, 简单方程法首先由Kudryashov等人提出, 并应用于一些偏微分方程的求解, 得到许多孤子解. 本文主要研究(2+1)维KP方程, 目的是求得它的精确行波解. 简单方程法是一种有效的求偏微分方程精确解的方法, 本文选取了比较熟悉的Bernoulli方程为简单方程, 求得KP方程的新解, 由于方程中的系数α,γ,ε是自由参数, 所以求得的解是一系列方程的解，对于研究水波运动有重要意义. 该方法的核心是平衡方程思想的运用. 本文用k=2去平衡, 而进一步的研究可以选k=3,k=4,…的情形, 求得KP方程更多的解. 本文所得到的解是新解与文献[16～17]中的解不同，所解的KP方程自由参数更多，得到更一般的解. 更重要的是运用本文的思想可以研究更多的非线性偏微分方程, 求得它们的精确解, 为工程计算，人口学，计算科学等学科的非线性偏微分方程模型研究工作提供求得此类精确解的理论依据.

[1] HIROTA R. Exact solution of Korteweg-de Vries equation for multiple collisions of solitons[J]. Phys Rev Lett, 1971,27(18):1192-1194.

[2] KUDRYASHOV N A. Exact solutions of the generalized Kuramoto-Sivashinsky equation[J]. Phys Lett A, 1990,147(5-6):287-291.

[3] LOU S. Symmetry analysis and exact solutions of the 2+1-dimensional sine-Gordon system[J]. J Math Phys, 2000,41(9):6509-6524.

[4] MARTINOV N, VITANOV N. On some solutions of the two-dimensional sine-Gordon equation[J]. J Phys A: Math Gen, 1992,25(5):L419-26.

[5] VITANOV N K, MARTINOV N K. On the solitary waves in the sine-Gordon model of the two-dimensional Josephson junction[J]. Z Phys B, 1996,100 (1):129-135.

[6] PANG J, BIAN C Q, CHAO L. A new auxiliary equation method for finding travelling wave solutions to KdV equation[J]. Appl Math Mech, 2010,31(7):929-936.

[7] MARTINOV N, VITANOV N. On the correspondence between the self-consistent 2D Poisson-Boltzmann structures and the sine-Gordon waves[J]. J Phys A: Math Gen, 1992,25(2): L51-6.

[8] VITANOV N K. Application of simplest equations of Bernoulli and Riccati kind for obtaining exact traveling-wave solutions for a class of PDEs with polynomial nonlinearity[J]. Commun Nonliner Sci Numer Simul, 2010,15(8): 2050-2060.

[9] KHADIJO R A, CHAUDRY M K. Exact solutions and conservation laws of Zakharov-Kuznetsov modified equal width equation with power law nonlinearity[J]. Nonlinear Anal: Real World Appl, 2012,13(4):1692-1702.

[10] KUDRYASHOV N A. Simplest equation method to look for exact solutions of nonlinear differential equations[J]. Chaos Solitons Fract, 2005,24(5):1217-1231.

[11] VITANOV N K. On modified method of simplest equation for obtaining exact and approximate solutions of nonlinear PDES: the role of the simplest equation [J]. Commun Nonlinear Sci Numer Simul, 2011,16(11):4215-4231.

[12] KUDRYASHOV N A, LOGUINOVA N B. Extended simplest equation method for nonlinear differential equations[J]. Appl Math Comput, 2008,205(1):396-402.

[13] VITANOV N K, DIMITROVA Z I. Application of the method of simplest equation for obtaining exact traveling-wave solutions for two classes of model PDEs from ecology and population dynamics[J]. Commun Nonlinear Sci Numer Simul, 2010,15(10):2836-2845.

[14] VITANOV N K, DIMITROVA Z I, KANTZ H. Modified method of simplest equation and its application to nonlinear PDEs[J]. Appl Math Comput, 2010,216(9):2587-2595.

[15] 刘玉堂, 李富志. 指数函数方法及其在非线性发展方程中的应用[J]. 计算机工程与应用, 2009,45(2):68-70.

[16] 丁玉敏, 冀小明. 利用EXP-函数展开法求解(2+1)-维KP方程[J]. 西南民族大学学报, 2008,34(6):1106-1110.

(编辑 沈小玲)

Application of Simplest Equations to Bernoulli Kind for Obtaining Exact Traveling-Wave Solutions for the (2+1)-Dimensional KP Equation

HELing-chao1,PANGJing1*,ZHAOZhong-long2

(1.College of Sciences, Inner Mongolia University of Technology, Hohhot 010051, China; 2.College of Sciences, China University of Mining and Technology, Xuzhou 221116, China)

Traveling-wave coordinate is used for transforming KP equation to a nonlinear ordinary differential equation. The traveling-wave solutions of KP equation are obtained by the method of the simplest equation when the simplest equation is the Bernoulli equation. The nonlinear ordinary equation is divided into two parts: part A contains the derivatives, and part B contains the rest of the equation. Then,balancing the highest powers of the polynomials for the parts A and B and a balance equation is obtained which depends on the kind of the simplest equation, the form of solution is determined. Finally, the new traveling-wave solutions of the KP equation are obtained.

method of simplest equation; (2+1)-dimensional KP equation; exact traveling-wave solutions

2013-04-01

国家自然科学基金资助项目(11071159); 内蒙古高等学校研究重点项目(NJ2214053)

*

,E-mail：pang_j@imut.edu.cn

O175.29

A

1000-2537(2014)04-0082-05