基于双曲正弦函数的新变步长LMS算法
2014-09-01罗海富
罗海富,刘 辉,张 旗
(湖南师范大学物理与信息科学学院,中国 长沙 410081)
基于双曲正弦函数的新变步长LMS算法
罗海富,刘 辉*,张 旗
(湖南师范大学物理与信息科学学院,中国 长沙 410081)
对自适应最小均方误差(LMS)滤波算法的步长选取问题进行了研究.在分析现有变步长LMS算法的基础上,通过对双曲正弦函数进行数学变化,构造步长因子u(n)与误差信号e(n)的函数,提出了一种基于双曲正弦函数的新变步长LMS算法,分析了参数a、b、c的选取对该算法性能的影响.仿真结果表明:该算法在收敛速度和稳态误差方面明显优于固定步长LMS算法及SVS-LMS算法.
LMS算法;步长因子; 变步长;稳态误差;收敛速度;双曲正弦函数
自适应滤波技术是现代信息处理技术的重要组成部分,被广泛地应用于智能天线、通信、生物医学、雷达信号处理等许多领域.1960年,美国斯坦福大学的Window和Hoff基于维纳滤波理论提出的最小均方误差(LMS)算法,由于其结构简单、性能稳定、计算复杂度低、易于硬件实现、鲁棒性好等特点,得到了广泛的应用[1-3].LMS算法是自适应滤波技术的经典算法,它基于最陡下降法的原理,以固定的步长因子u沿着权值梯度估值的负方向进行搜索,直至达到权值最优,从而实现均方误差意义下的自适应滤波[4].所以在设计自适应滤波器时,不需要预先知道输入信号和噪声的统计特性的先验知识,也不需要精确的设计信号处理系统的参数,特别地在滤波过程中,输入信号是非平稳信号时,滤波器也能够自我进行调节适应.
然而传统LMS算法的收敛性不好,且收敛速度和稳态误差之间存在矛盾[5],为了克服这一缺点,人们相继提出了很多改进的变步长LMS算法[5-9],即采用变步长来实现矛盾间的平衡.文献[5~8]指出,衡量自适应滤波器算法性能的4个重要技术指标是收敛速度、算法计算复杂度、时变跟踪能力、稳态失调,即一种好的算法应该具备:跟踪速度快、收敛速度快、计算复杂度小、抗噪性能强、收敛精度高的特点.
1 LMS算法
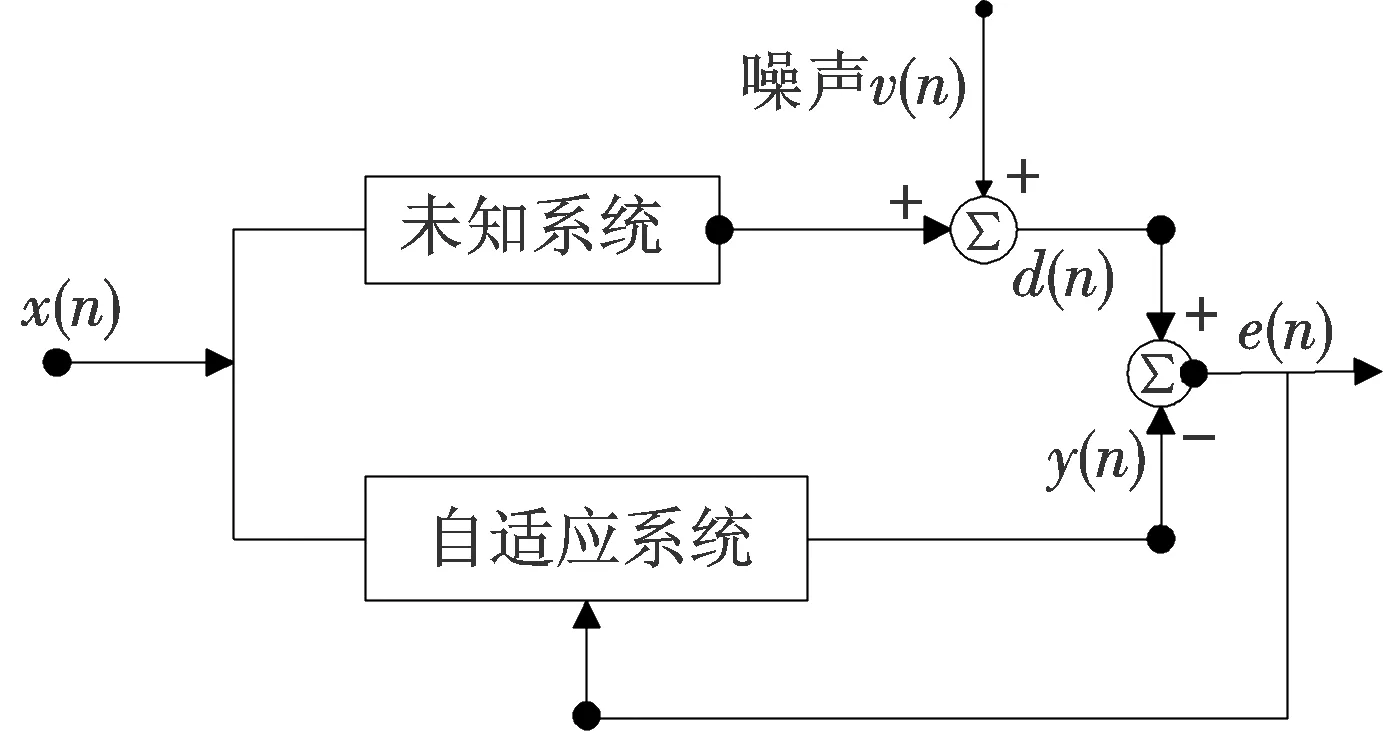
图1 自适应滤波器的滤波原理图Fig.1 Principle of adaptive filter
自适应滤波器的滤波原理如图1所示,其中x(n)为实际输入信号,v(n)为噪声信号,y(n)为输出信号,d(n)为期望信号,e(n)为误差信号.
LMS算法采用输出信号与期望信号的最小均方误差作为代价函数[10],传统固定步长LMS算法步骤[11]如下:
1)初始化权值系数:W(0)=0, 0 2)对输入信号x(n)进行滤波,产生期望响应及误差信号: y(n)=WT(n)*x(n), (1) e(n)=d(n)-y(n). (2) 3)更新抽头权向量: W(n+1)=W(n)+2*u*x(n)*e(n). (3) 4)返回重复步骤2)至步骤4). 其中u为步长,它的取值对LMS算法的性能起着决定性的作用,收敛条件为[12]:0 u(n)=β*(1/(1+exp(-∂*|e(n)|))-0.5). (4) 使得SVS-LMS算法比传统固定步长LMS算法的收敛速度更快. 2.1 改进的LMS算法 文献[5~7]提出了对步长因子u的调整原则,即在算法的初始收敛阶段或在自适应系统参数发生变化时,步长因子u的值应该较大,从而使得算法具有较快的收敛速度和对时变系统的跟踪速度;而在算法达到收敛后,此时系统的权值矢量已接近最优值[14],步长因子u应该保持较小的值以达到很小的稳态误差. 本文在满足上述调整原则的基础上,根据文献[5]所提出的算法的图像曲线特征,通过对双曲正弦函数的研究,提出了一种新的基于双曲正弦函数的变步长算法.双曲正弦函数的表达式为: (5) 图2 双曲正弦函数Fig.2 Hyperbolic sine function 图2为f(x)的图像,由图可知,它具有对原点对称的性质.简单的对双曲正弦函数进行变化,并引入控制取值范围的系数a和控制图像形状的系数b、c,变换后的函数表达式为: u(n)=a*|sinh(b*e(n)c|, (6) 通过Matlab对公式(6)进行函数图形绘制,由图3 可知,当e(n)趋近0时,u(n)也趋近0,随着e(n)的变化,u(n)呈非线性变化,函数底部平滑,u(n)随e(n)变化缓慢.可见其满足步长特征. 由此得到本文基于双曲正弦函数的变步长LMS算法为 (7) 2.2 参数分析 保持b、c不变,对a进行调整,可以看出:当b=5,c=1,a分别取0.000 6,0.000 3,0.000 1时,u(n)与e(n)的关系如图4所示.由图4可知,a越大,u的初始值就越大,随着a的增大,函数的开度增大. 图3 变化后的函数图像Fig.3 The image function changes after 图4 a变化时,u(n)与e(n)的关系Fig.4 Changes of a, u(n) and e(n) relationship 保持a、c不变,对b进行调整,可以看出:当a=0.000 6,c=1,b分别取4,5,6时,u(n)与e(n)的关系如图5所示.由图5可知,b越大,初始阶段的u也越大,函数的开度也增越大. 保持a、b不变,对c进行调整,可以看出:当a=0.000 6,b=5,c分别取1,2,3时,u(n)与e(n)的关系如图6所示.由图6可知,函数在e(n)=±1时,最大值保持不变,函数凹凸程度发生变化. 图5 当b变化时,u(n)与e(n)的关系Fig.5 Changes of b, u(n) and e(n) relationship 图6 当c变化时,u(n)与e(n)的关系Fig.6 Changes of b, u(n) and e(n) relationship 从上面对参数a,b,c分别取不同值的分析可知,a的最佳取值范围是(0,0.01),b的最佳取值范围是(0,8),c的最佳取值是1(减少计算复杂度),不同的取值将对算法的收敛速度和稳态失调性能产生影响,选择合适的a,b,c,就可以保证0 图7 3种算法的收敛曲线Fig.7 The convergence curves of three kinds of algorithms 利用Matlab工具将本文算法与传统固定步长LMS算法、SVS-LMS算法进行仿真对比实验,实验条件规定为:输入信号为信号幅度为1的周期性正弦信号,方差为0.04的标准高斯白噪声为噪声信号,自适应滤波器的的滤波阶数k=2,输入信号抽样点数为N=1000.滤波器的算法分别选用传统固定步长的LMS算法、文献[15]提出的SVS-LMS算法及本文提出的算法.设仿真时固定步长LMS算法的步长u=0.01;SVS-LMS算法的参数选择为α=1.5,β=1;本文算法的最优参数选择为a=0.000 6,b=5,c=1;以下分别从收敛性、计算量、输出结果3个方面对上述3种算法进行仿真分析. 3.1 收敛性能 图7分别给出了3种算法的收敛曲线.由图可知传统固定步长LMS算法在第100个采样点收敛,SVS-LMS算法在第90个采样点收敛,而本文算法在第30个采样点收敛.因此本文提出的算法比传统固定步长LMS算法、SVS-LMS算法的收敛速度更快. 3.2 算法的计算复杂度 表1为2种算法的步长函数复杂度的比较,从中可以看出本文的算法复杂度与其他算法的复杂度相近. 表1 2种算法的计算复杂度比较 3.3 输出结果 由图8可知,本文算法的输出信号比固定步长LMS算法及SVS-LMS算法的输出信号更接近期望信号. (a)期望信号 (b)3种算法输出信号 综上所述,传统固定步长LMS算法由于对e(n)缺乏调节能力,导致算法在收敛性与稳定性方面存在矛盾.本文根据变步长LMS算法的步长调节原则,通过建立步长因子与误差信号的双曲正弦函数关系从而改进了LMS算法,并对参数的设定进行了分析仿真.通过仿真对比表明:作者提出的算法能够有效地提高收敛速度,同时在稳态性能方面也有一定的优越性. [1] STEPHEN W P. Steepest algorithm for neural network controllers and filters [J].IEEE Trans Neural Networks, 1994,5(2):198-212. [2] KWONG R H, JOHNSTON E W. Variab lestep size LMS algorithm [J].IEEE Trans Signal Processing, 1992,40(7):1642-1663. [3] BELLOFIORE S, BALANIS C A, FOUTZ J,etal. Smart-antenna systems for mobile communication net works part1: overviewand antenna design [J]. IEEE Antenn Prop Mag, 2002,44(3):145-154. [4] 杨 宇,施未来.变步长LMS自适应滤波算法研究[J].江苏教育学院学报, 2011,27(1):9-10. [5] 覃景繁,欧阳景正.一种新的变步长自适应滤波算法[J].数据采集与处理, 1997,12(3):171-194. [6] 高 鹰,谢胜利.一种变步长LMS自适应滤波算法及分析[J].电子学报, 2001,29(8):1094-1097. [7] 李建平,蒙建波.基于双曲函数的变步LMS 算法及其分析[J].传感器与微系统, 2011,30(5):127-129. [8] 罗小东,贾振红,王 强.一种新的变步长LMS自适应滤波算法[J].电子学报, 2006,34(6):1123-1126. [9] 靳 翼.变步长LMS自适应均衡算法研究及其在DSP上的实现[D].成都:电子科技大学, 2010. [10] 李洪兵.时域变步长最小均方误差自适应滤波算法研究[D].西安:空军工程大学, 2008. [11] 龚耀寰.自适应滤波时域自适应滤波和智能天线[M ]. 2版.北京:电子工业出版社, 2003. [12] BELLOFIORE S, BALANIS C A, FOUTZ J. Smartantenna system for mobile communication net works part2:beam for ming and net work through put [J]. IEEE Antenn Prop Mag, 2002,44(4):106-114. [13] 何振亚.自适应信号处理[M].北京:科学出版社, 2002. [14] 谷源涛.LMS算法收敛性能研究及应用[D].北京:清华大学, 2004. [15] SRISTI P, LU W S, ANTONIOU A. A new variable step-size LMS algorithm and its application in subband adaptive filtering for echo cancellation[J].IEEE Int Sympos, 2012,2(6):721-72. (编辑 陈笑梅) New Variable Step-Size LMS Algorithm Based on Hyperbolic Sine Function LUOHai-fu,LIUHui*,ZHANGQi (College of Physics and Information Science, Hunan Normal University, Changsha 410081, China) The adaptive minimum mean square error (LMS) filtering algorithm step was studied. Based on analyzing the existing variable step size LMS algorithm, through mathematical changes on the hyperbolic sine function, a function is set up between step size factoru(n) and the error signale(n) function, and a new variable step size LMS algorithm is proposed based on the hyperbolic sine function, and the influence of parametera,b,cvalue on the performance of the algorithm was analyzed. Simulation results show that the proposed algorithm significantly outperforms the fixed step size LMS algorithm and SVS-LMS algorithm in convergence speed and steady-state error. LMS algorithm; step factor; variable step-size; seeady-state error; convergence rate; hyperbolic sine function 2013-03-10 湖南省自然科学基金资助项目(12JJ3071) * ,E-mail:liuhui1366@126.com TN911.72 A 1000-2537(2014)04-0062-042 基于双曲正弦函数的新变步长LMS算法
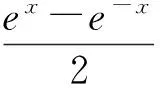

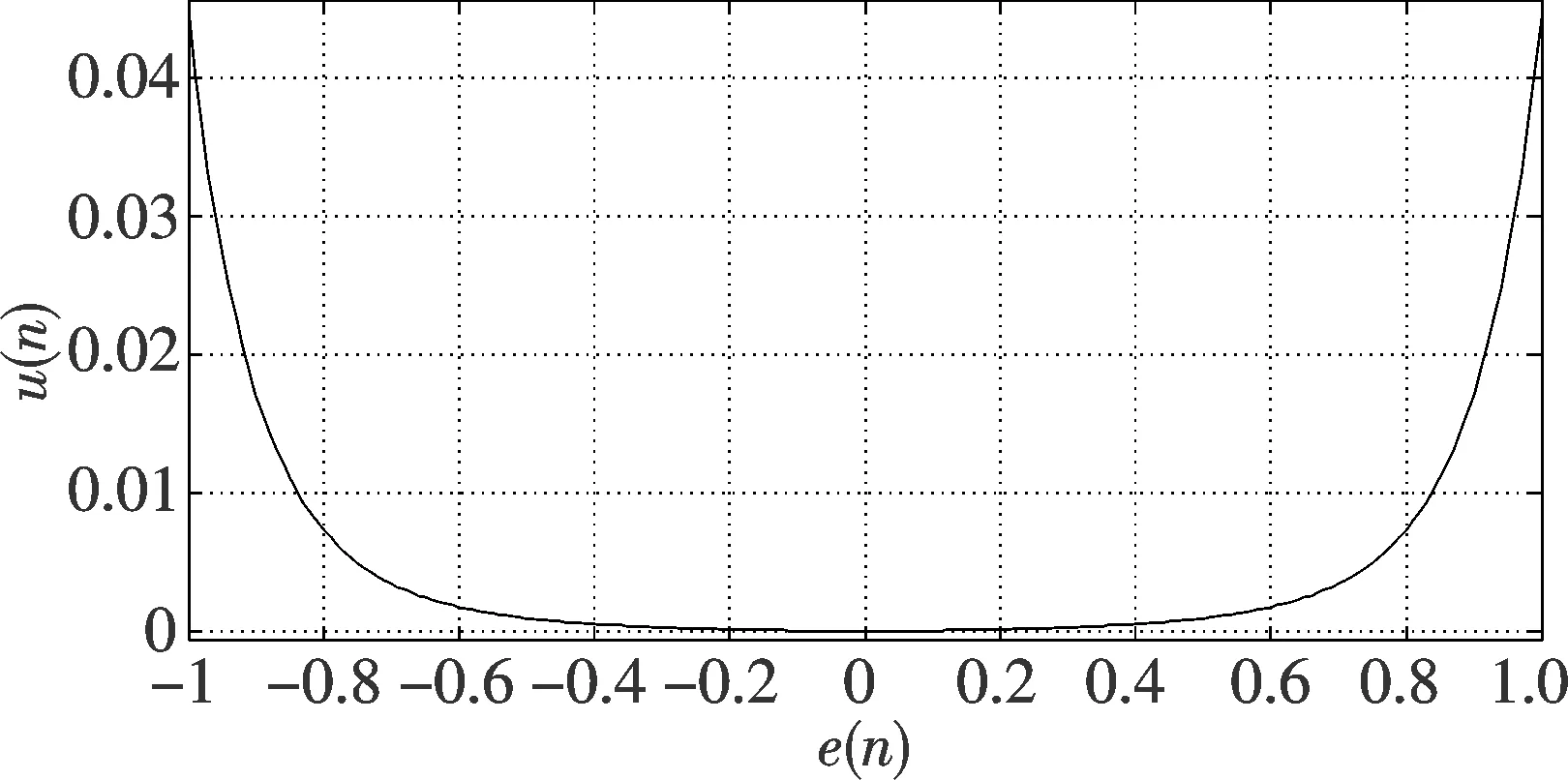



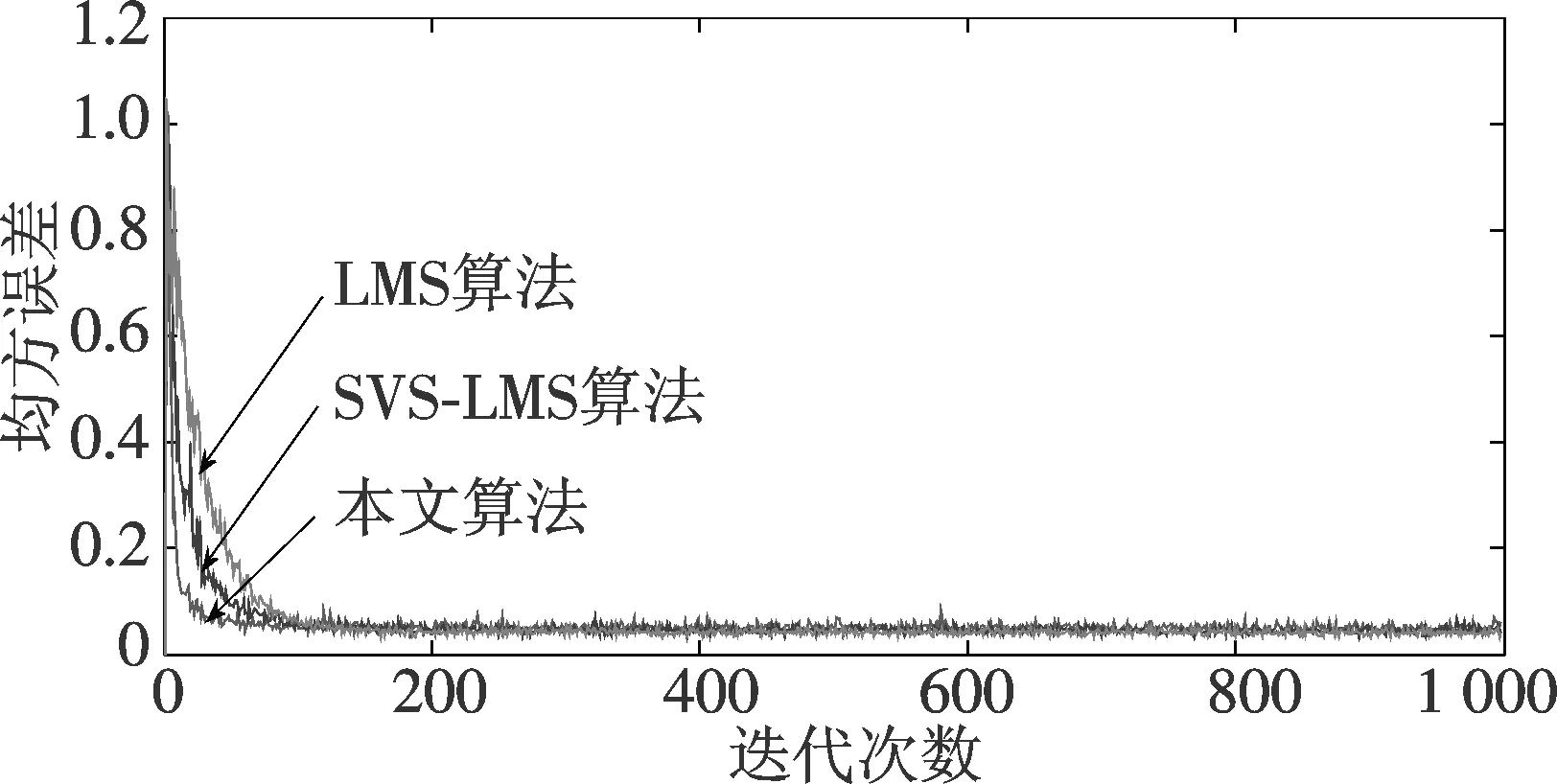
3 仿真与结果分析


4 结论
