单极子声源平面空间有源降噪的最短距离

姚加飞，郭 爽

（1.重庆大学 输配电装备及系统安全与新技术国家重点实验室，重庆400044；2.重庆大学 建筑设计研究院，重庆400044)

单极子声源平面空间有源降噪的最短距离

姚加飞1，2，郭 爽1

（1.重庆大学 输配电装备及系统安全与新技术国家重点实验室，重庆400044；2.重庆大学 建筑设计研究院，重庆400044)

以单极子噪声源与单极子抗噪声源组成的声场为研究对象，得出用单极子抗噪声源控制单极子噪声源，使两声源所在的平面空间内的总声功率最小时两声源本身的声强的关系。并计算空间内任意一点的径向平均有功声强。得出最小径向平均有功声强与声源的频率和两声源的距离有关，在一定频率下，两声源距离越近，控制后的径向平均有功声强越小，距离一定的情况下，频率越小，径向平均有功声强越小。通过仿真实验进行验证，并最终得到某些低频噪声达到全空间消声时噪声源与抗噪声源的最短距离。

声学；单极子；有源噪声控制；径向有功声强；Matlab仿真

文献[3]、文献[4]针对抗噪声源时滞引起的尖峰噪声的抑制提供了解决的方法。对于单极子声源的有源控制，文献[5]是以噪声源、抗噪声源总的辐射声功率最小为控制目标，并通过调节抗噪声源的复强度来实现，计算在抗噪声源的作用下的声场总的声功率与噪声源单独存在时的声功率比值，得出最小声功率与两声源的频率和距离有关，频率越小，距离越近，最小声功率越小。文献[6]中解出了管道声场引入单极子抗噪声源后的声能量密度与未引入抗噪声源前的比值，说明了单极子管道有源降噪系统的噪声源，抗噪声源总在进行着能量的交换，当噪声源与抗噪声源距离很远时，降噪后的声场呈能量的空间转移机制，但若两者相距很近，则呈多极子场机制。以上文献通过声功率，声能量密度等方面说明了单极子声源的有源降噪的降噪程度与声源的频率和两声源的距离有关。对于降噪效果的说明，声强更有优势。有功声强表示垂直于传播方向上波阵面的声能量流，径向有功声强表示空间内任意一点与声源连线方向上的声能量流。声强能够量化降噪效果，从而比声功率和声势能密度更好地说明降噪程度。值得一提的是，在工业噪声源的快速分析和定位中，声强分析对对测试环境没有特殊的声学要求，因此对声强进行分析更有利于实践应用[7]。径向有功声强更容易用公式表示，故本文采用空间内任意一点的径向有功声强来具体说明降噪效果。

本文以单极子噪声源与单极子抗噪声源所在的平面空间为研究对象，以径向平均有功声强最小为控制目标。通过声场内的声功率最小的得出点声源本身的声强的关系，再将此结论代入径向平均有功声强公式。从理论上阐述了声场中有源降噪效果与两声源的距离和频率的关系，而且通过仿真验证了达到平面空间全空间消声的噪声源与抗噪声源的最短距离。

1 两声源声强的关系

如图1，设空间内有两个点声源，一个为噪声源，另一个为抗噪声源。具体说明见表1。

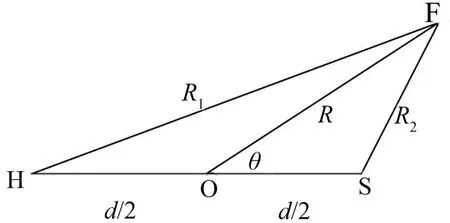
图1 噪声源，抗噪声源，空间内任意一点的空间分布

由于噪声源、抗噪声源同时存在时，每个声源的振动状态都要受到另一个声源辐射声场的影响，因此空间内任意一点F所在声压为

其中p1，p2分别为噪声源，抗噪声源单独存在时F点的声压[8]，且

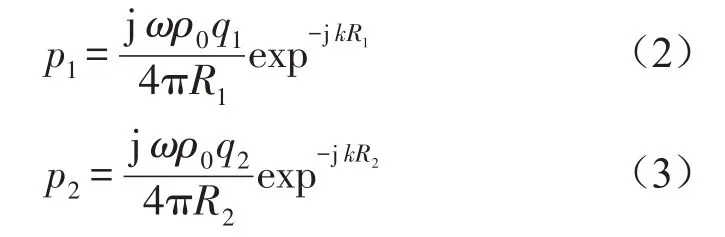
其中ρ0为空气密度，k为声波波数。且波数c0为声波在空气中的传播速度，ω是声传播的角频率。ω=2πf，故k与f成正比。

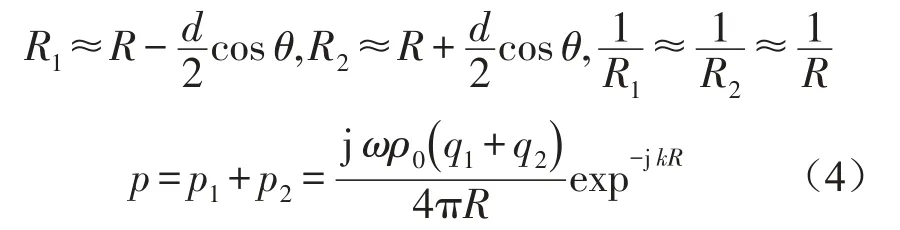
如果要求噪声源与抗噪声源的总声功率比原始的声功率降低，则[9]

将式(1)—(4)式代入式（5）可求出最佳抗噪声源强度为

（6）式是为达到空间内噪声源与抗噪声源总的辐射声功率最低时的两个声源本身的声强的比值。

2 空间内一点径向有功声强

上述声场中任意一点的径向速度为

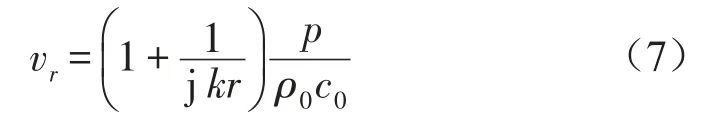
将式（7）代入声强公式则任意一点的径向有功声强

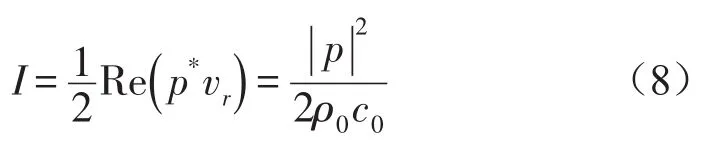
在空间内辐射的总声功率最低时空间内任意点声强即将式（6）代入式(9)可得

代入（4）式可得

表1 图1中各点的位置介绍

当声场中只有噪声源，而无抗噪声源时

3 声强与频率和距离的关系

由声强级公式L=10log(I/I0)，其中I0为基准声强且I0=1 pW/m2。则减少的声强

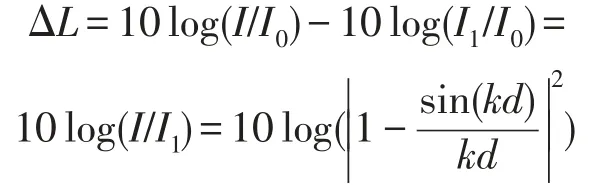
图2为ΔL的波形图。纵坐标表示随着k×d的变化空间内任意一点的分贝数降低的情况。

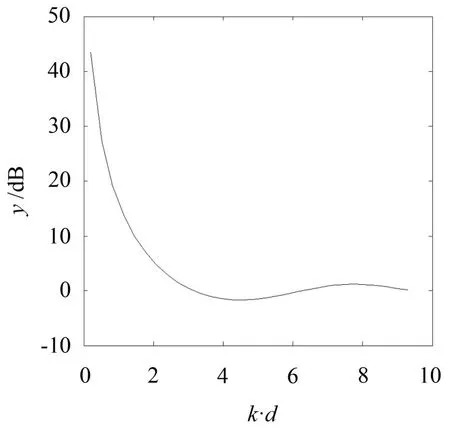
图2 降噪量随k×d的变化

图2中值表示引入抗噪声源后声场中的声强比只存在噪声源时降低了。并且k×d乘积越小降噪效果越明显。当k×d越来越大时，降噪效果越来越差。k与f成正比，故随着频率和距离的不断增大，降低的分贝数逐渐减少。保持频率不变，降噪量随距离的变化如图2所示。

由图3可知，随着两声源距离的增大，降低的分贝数逐渐减少。随着频率的增加，达到相同降噪量时两声源的距离减少。因此，频率越大，能够降噪达到相同降噪效果的距离越小。

4 仿真实验

仿真研究一空间的整体降噪情况。设噪声源的本身的声强q1=46dB，下列4组图分别为f=200 Hz，d=0.5 m；f=200 Hz， d=1 m；f=400 Hz，d=0.5 m；f=400 Hz，d=1 m某一平面空间内的声强的仿真图形，见图4—图7。

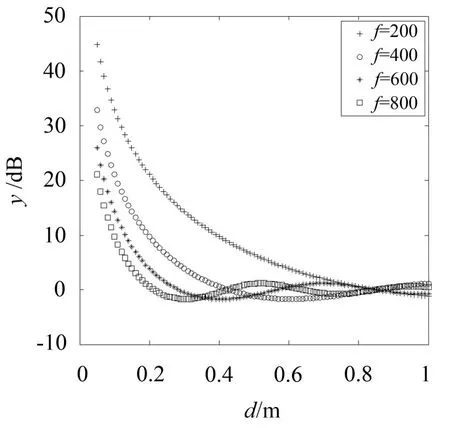
图3 保持频率不变降噪量随距离的变化

由图7可得两声源在相同的距离下，频率增大时，平面空间的深色的面积增多了，声强增大了保持频率不变当两声源距离增大时，图中深色区域的面积减小了，故降噪的水平降低了。验证了上述理论。当两声源距离降低到一定程度时，平面空间的声强值接近为零。图8(a)，(b)，(c)，分别为当f=100 Hz时，达到平面空间完全消声的最短距离为0.2 m，f=300 Hz达到平面空间完全消声的最短距离为0.10 m，f=500 Hz时，达到平面空间完全消声的最短距离为0.01 m。多次仿真实验验证得各个不同频率下的达到平面空间完全消声的最短距离如表2所示。

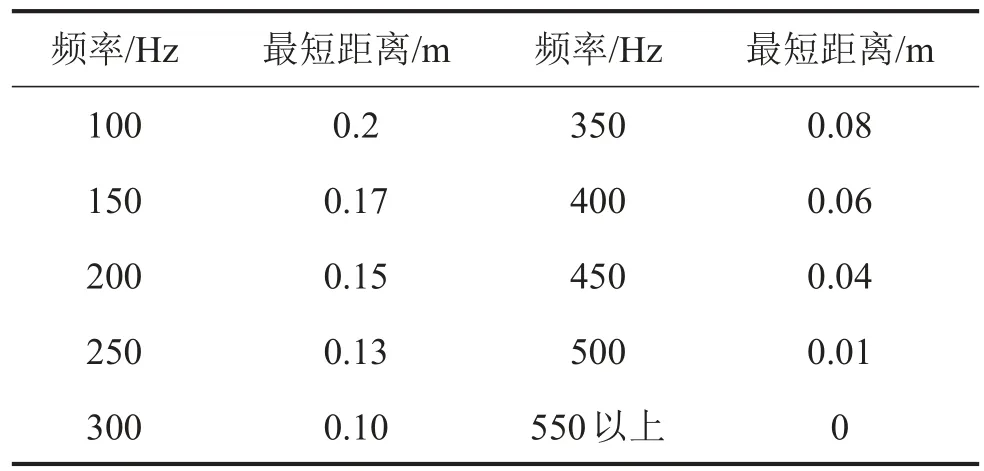
表2 各频率达到完全消声的最短距离

当f＞550 Hz时，只有噪声源与抗噪声源完全重合时（d=0）才能达到完全降噪。

5 结语

本文通过引入径向有功声强公式阐明了最简单的声源：单极子声源的降噪情况。得出在一定频率下，两声源距离越近，控制后的声强越小。对于确定的噪声源与抗噪声源间距，频率越低，声强越小。同时仿真得出了在某些频率下。达到全空间消声时噪声源与抗噪声源的最短距离。

图4 f=200 Hz，d=0.5 m时平面空间内的声强分布图

图5 f=200 Hz，d=1 m时平面空间内的声强分布图

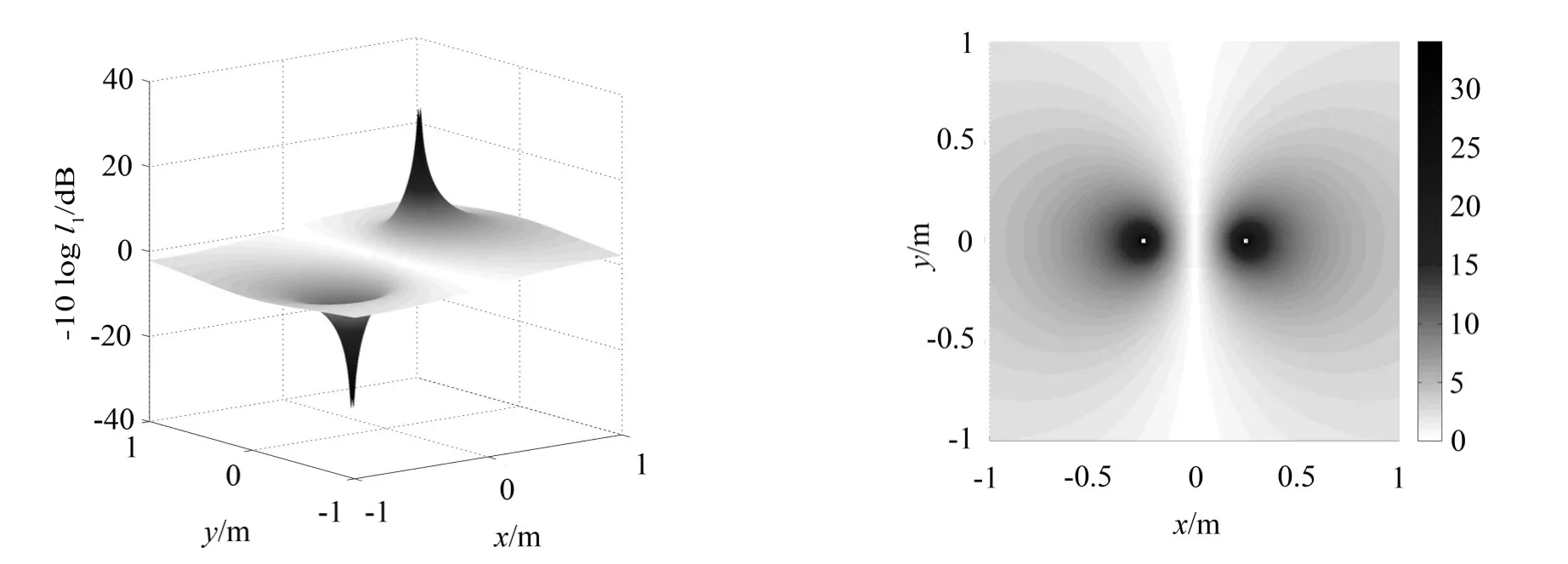
图6 f=400 Hz，d=0.5 m时平面空间内的声强分布图

图7 f=400 Hz，d=1 m时平面空间内的声强分布图

图8 （a）f=100 Hz，(b)f=300 Hz，(c)f=500 Hz达到完全消声的最短距离分别为d=0.2 m、d=0.1 m、d=0.01 m

[1]王进军，陈克安.有源噪声控制的现状及展望[J].现代振动与噪声技术，2005：65-67.

[2]陈端石.噪声主动控制研究的发展与动向[J].应用声学，2001，2，20(4)：l-5.

[3]姚加飞，卢 萍.抗噪声源时滞引起的尖峰噪声的抑制[J].噪声与振动控制，2012(3)：108-112.

[4]姚加飞，罗梦莹.抗噪声源时滞引起的尖峰噪声的分析及抑制[J].噪声与振动控制，2013(2)：148-151.

[5]陈克安.有源噪声控制[A].北京：国防工业出版社，2003，149-152.

[6]田 静.关于单极子次级声源管道有源降噪能量机制的理论分析[J].声学学报，1992，17(5)：369-374.

[7]朱从云，赵则祥，李春广，黄其柏.噪声控制研究进展与展望[J].噪声与振动控制，2007，6(3)：1-8.

[8]陈卫松，浦宏杰，邱小军.应用于有源声辐射控制的一种组合次级声源[J].应用声学，2010，3(5)：169-177.

[9]李 双，陈克安.有源声学结构次级声源的布放规律研究[J].机械科学与技术，2006，11(25)：1352-1357.

The Shortest Distance of Monopole Noise Sources in Plat Space underActive Noise Control

YAO Jia-fei1,2,GUOShuang1

（1.State Key Laboratory of Power Transmission Equipment&System Security and New Technology, Chongqing University,Chongqing 400044,China; 2.Institute ofArchitectural Design,Chongqing University,Chongqing 400044,China）

This article studies the sound fields of the monopole noise source and monopole anti-noise source.The relationship between the sound intensity of the noise source and the sound intensity of the anti-noise source under the condition of the least sound power in the plat sound field is obtained.In addition,the radial average active sound intensity at any point in the sound field is calculated,which is found to be related to the frequency of the sound source and the distance between the two sources.For a fixed frequency,the radial average active sound intensity decreases with the distance between the two sources increasing after the control.For the fixed distance between the two sources,the radial average active sound intensity decreases with the frequency decreasing after the control.Through the MATLAB simulation,the shortest distance between the noise source and anti-noise source when the sound intensities of some low-frequency noises in the whole space vanish is obtained.

acoustics;monopole;active noise control;radial active sound intensity;MATLAB simulation

1006-1355(2014)03-0026-04

TB52+6；X593

A

10.3969/j.issn.1006-1335.2014.03.006

相较于传统的吸声、隔声，如消声器等有源消声，则采用一个新的噪声场与原有的噪声场相消[1]，不仅与无源降噪互补，抑制低频噪音，而且避免无源降噪所需设备较为笨重，体积庞大，价格昂贵等缺陷[2]，这是近年噪声控制领域的研究热点。

2013-06-14

姚加飞，男，重庆人，副教授，研究生导师，研究方向为控制理论与控制工程

郭 爽（1988-），女，吉林人，硕士研究生，研究方向为控制理论与控制工程。

E-mail:1051222919@qq.com