基于有限差分法的变截面旋转梁弯曲振动
2014-08-31朱由锋朱由国
朱由锋,朱由国
(1.山东科技大学 机械电子工程学院,山东 青岛266590;2.青岛胶南绿茵环保科技有限公司,山东 青岛266400)
基于有限差分法的变截面旋转梁弯曲振动
朱由锋1,朱由国2
(1.山东科技大学 机械电子工程学院,山东 青岛266590;2.青岛胶南绿茵环保科技有限公司,山东 青岛266400)
根据哈密尔顿原理建立旋转梁的弯曲振动方程,运用有限差分方法对旋转梁的动力方程进行离散处理,得到旋转梁的质量和刚度矩阵。借助MATLAB振动工具箱对系统的弯曲振动进行模态分析,得到圆形、矩形和叶片类型三种变截面旋转梁的固有频率,并与相关文献进行比较。在差分离散矩阵的基础上,建立旋转梁的线性定常状态空间方程。运用MATLAB振动工具箱对旋转梁的自治系统和非自治系统进行仿真,分别求得旋转梁的时间位移曲线和相轨迹。最后对非自治系统的旋转梁进行频域分析,得到幅频特性和相频特性曲线。
振动与波;变截面;旋转梁;有限差分;固有频率;状态空间
1 差分方程的建立
1.1 微分方程的建立
旋转梁模型如图1所示,x轴为几何轴线,y轴为垂直轴,与重力方向一致。z轴为旋转梁的水平方向。R为旋转梁的轮毂半径,悬臂梁沿轮毂中心的水平轴旋转。梁的角速度为Ω,长度为L。截面为圆形、矩形或者叶片类型,截面积沿x轴方向减小。

图1 旋转梁模型
旋转梁的势能为

f(x)为旋转梁的离心力,可以表示为
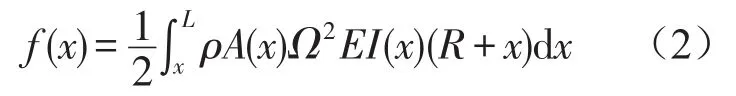
旋转梁的动能为

根据哈密尔顿原理

上面所建立的运动方程是以体系静力平衡位置为基线建立的,但质量上尚有重力,现在考虑重力的作用建立旋转梁的弯曲振动微分方程为

式中ρ——旋转梁的密度,kg/m3;A——旋转梁的截面面积,m2;E——旋转梁的杨氏模量,MPa;I——旋转梁的惯性矩,cm4;µ——旋转梁在y向的变形量,m。
1.2 有限差分离散
旋转梁为悬臂梁,边界条件为
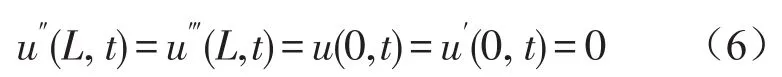
首先以x方向的4阶导数为例进行差分处理。根据泰勒的展开形式,运用2阶中心差分后,可以得到x方向各次导数的一般差分形式。根据一次差分公式和边界条件可以得到
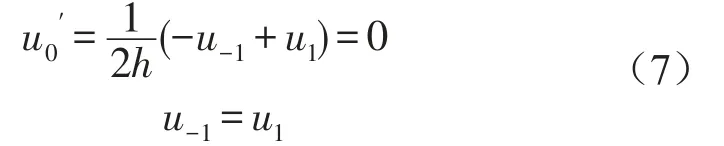
根据二次、三次差分公式和边界条件
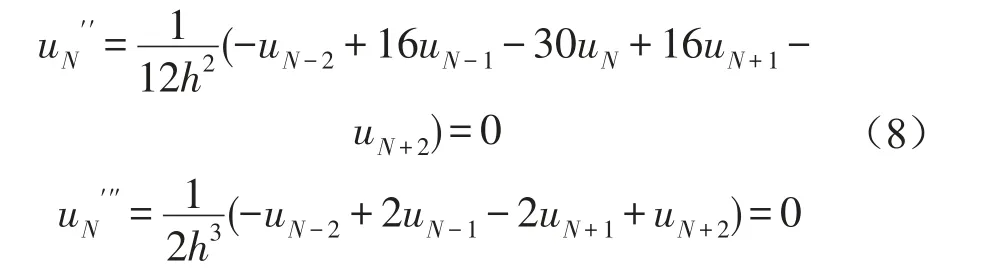
求解后得到

最后计算求得四阶导数的差分
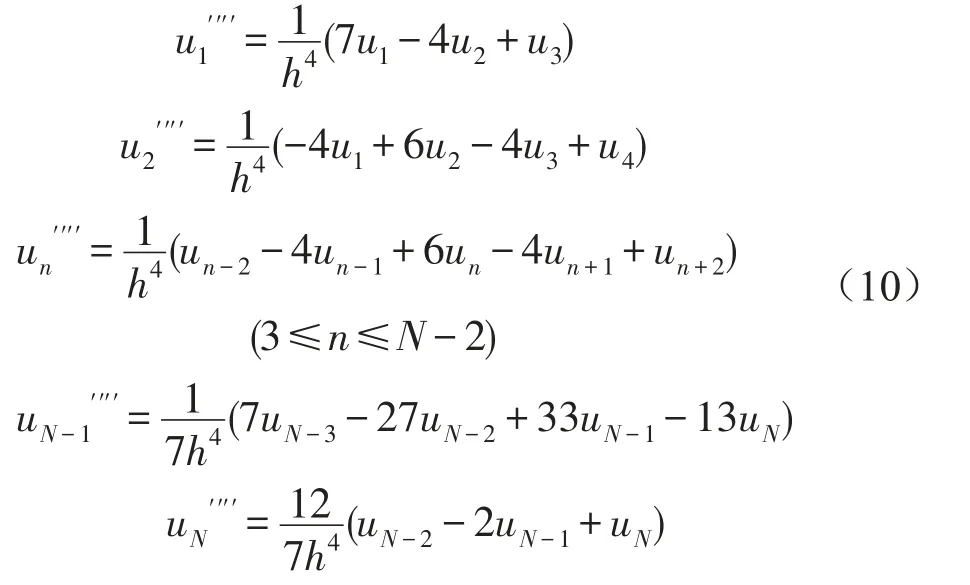
同理,1阶导数的差分为
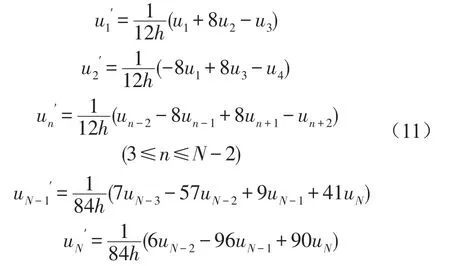
2阶导数的差分为

3阶导数的差分为


2 旋转梁的固有频率
将差分公式代入微分方程中的微分项后,得到旋转梁的矩阵表达式

分析模态时,取F=0。 K为不对称刚度矩阵,即使对x进行矩阵行变换也无法解耦,所以不能用传统的叠加法进行求解。可运用MATLAB振动工具箱的vtb4-3进行求解。选择旋转梁的参数为

为了方便分析,部分参数进行无量纲处理
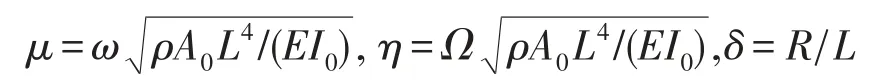
本文对三种变截面旋转梁的固有频率进行了研究。第一种为圆形截面梁,参数为
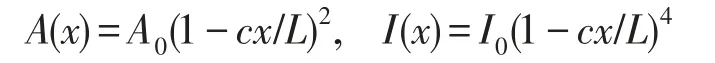
0≤c<1为旋转梁的锥度比。表1为差分节点个数对固有频率的影响。考虑到计算速度的因素,选择N=200作为后续计算的节点。表2为不同转速下的固有频率,并与文献[11]进行了比对。
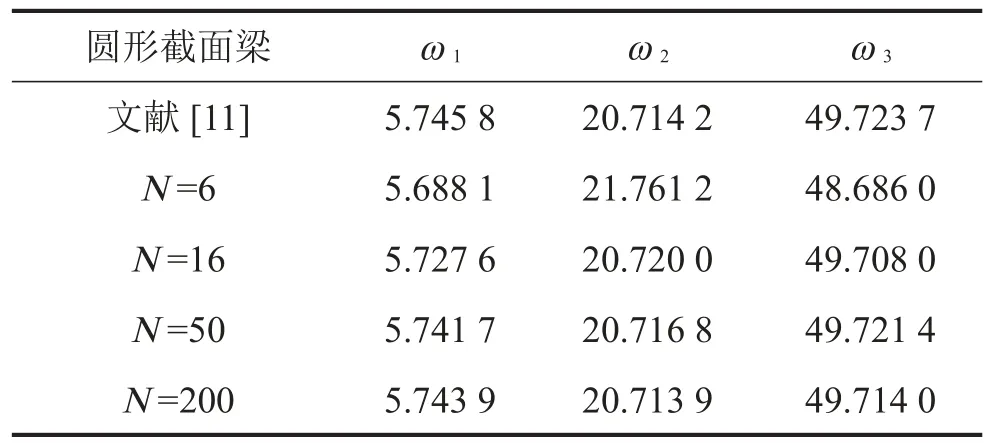
表1 差分结点个数N对数值的影响(c=0.5,η=3)

表2 圆形截面梁的固有频率(c=0.5)
第二种为矩形截面梁,参数为
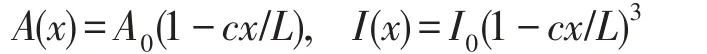
0≤c<1为旋转梁的锥度比。表3为不同转速下的固有频率,并与文献[11]进行了比对。
第三种为叶片截面梁,参数为

表4为不同转速下的固有频率,并与文献[11]进行了比对。图2(a)为η=5时圆形截面旋转梁的锥度比对固有频率的影响。图2(b)为η=5时矩形截面旋转梁的锥度比对固有频率的影响。随着锥度比的增加,3阶固有频率呈快速下降趋势,2阶固有频率略有下降,1阶固有频率有小幅的提高。锥度比在接近1的区域极少应用。
3 旋转梁的振动仿真
根据前面进行的有限差分离散简化,旋转梁就转化为线性定常系统[12,13]问题,状态空间表达式为

其中

然后利用MATLAB振动工具箱,对输入条件进行适当控制,可以得旋转梁的时域频域特性。以圆形截面梁为例,不考虑重力的作用,旋转梁为自治系统。选取c=0.5,旋转梁末端振动位移为0.046 m,其它节点的初始位移依据主振型进行计算得出。图3(a)、3(b)分别为旋转梁的自治系统的位移时间曲线和相轨迹。旋转梁末端以(0,0)为中心周期性振动,振动周期与初始位移无关,振动的幅度和速度由初始位移条件决定。旋转梁的其它位置的振动趋势与末端相似,只是振幅和速度有差异。

表3 矩形截面梁的固有频率(c=0.5,δ=2)
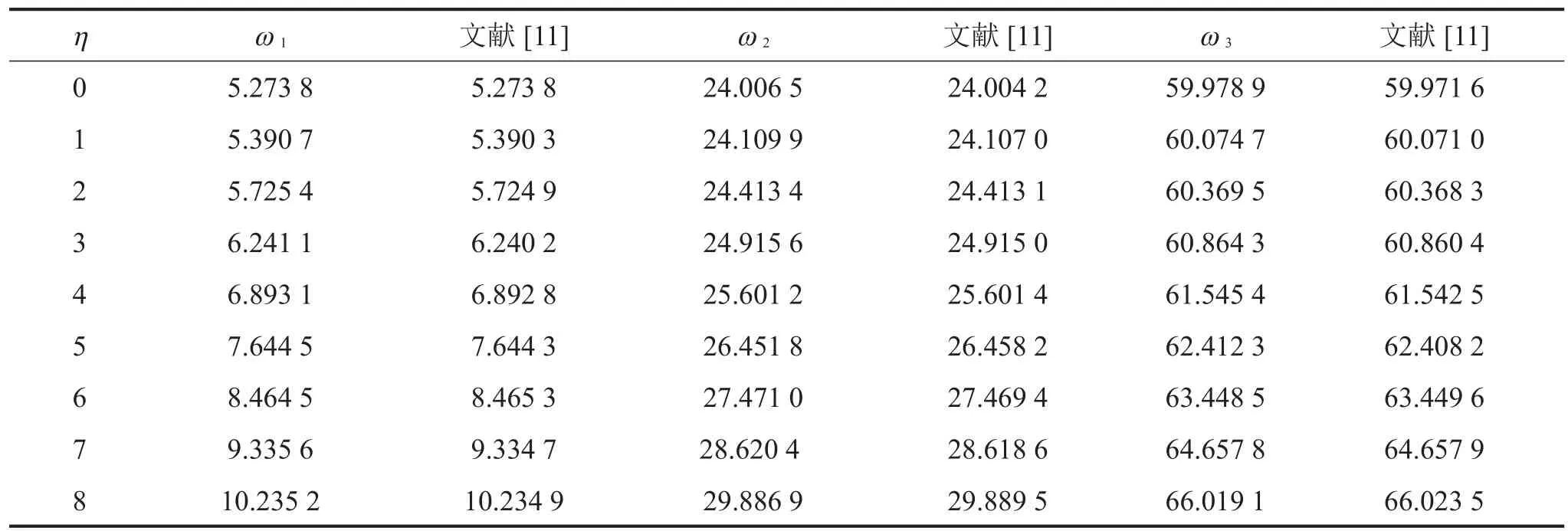
表4 叶片截面梁的固有频率

图2 锥度比对固有频率的影响

图3 旋转梁的自治振动
旋转梁的重力随旋转角度周期性改变,考虑到重力的作用,旋转梁为非自治系统。以圆形截面梁为例,选择c=0.5,η=7,0初始位移条件时,可以得到图4、图5。图4(a)、4(b)分别为旋转梁的非自治系统的位移时间曲线和相轨迹。旋转梁末端以(0,0)为中心周期性振动,振动的周期由旋转的速度决定,但由于受余弦力激振力的作用,在每个周期都会有扰动。
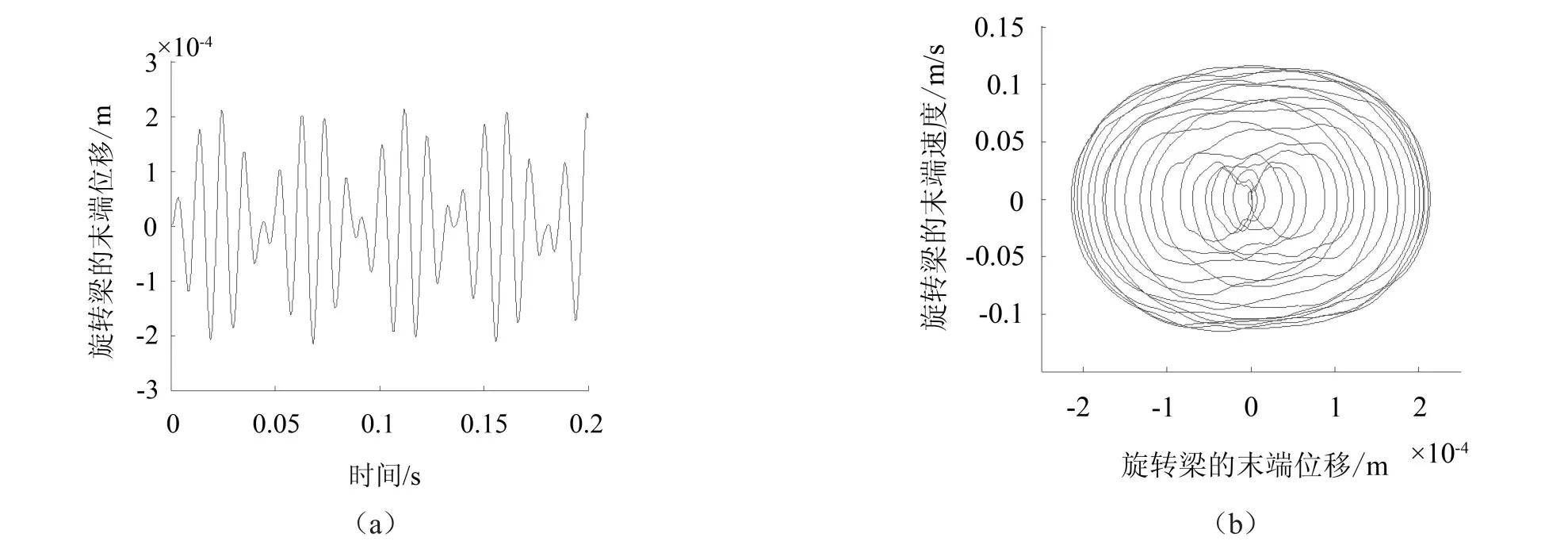
图4 旋转梁的非自治振动

图5 旋转梁的频域分析
图5(a)、5(b)为非自治系统时旋转梁末端的幅频特性和相频特性。在无量纲频率η=7时,旋转梁有明显的振幅增加。在η=9.076 2时为旋转梁的一阶固有频率,旋转梁的振幅也有明显增加。在旋转梁的2阶固有频率附近,旋转梁的振幅也有所增加,但不是很明显。在5(b)的相频特性图上可以看出,在η=7、1阶和2阶固有频率附近,旋转梁的相位都有明显的改变。矩形截面和叶片截面旋转梁的时域频域仿真分析与圆形截面旋转梁类似,由于篇幅关系,在此不详述。
4 结语
利用有限差分离散和MATLAB振动工具箱,对圆形截面、矩形截面和叶片截面三种不同类型的旋转梁进行模态分析,求得不同转速及锥度比下的弯曲固有频率。通过状态空间分析法对自治系统和非自治系统进行了仿真分析,绘制旋转梁的位移时间响应曲线和相轨迹。对非自治系统旋转梁进行了频域分析,得到其幅频特性和相频特性曲线。本文仿真结果与文献[11]的结果进行比较,验证了有限差分法和状态空间分析法的有效性,为分析旋转梁的动力学特性,提供了一种可供选择的有效计算方法。
[1]Chung J,Yoo H H.Dynamic analysis of rotating cantilever beam by using the finite element method[J].J.Sound Vib.,2002,249:147-164.
[2]Bazoune A.Effect of tapering on natural frequencies of rotating beams[J].Shock Vib.,2007,14:169-179.
[3]Fox C H J,Burdess J S.The natural frequencies of a thin rotating cantilever with offset root[J].J.Sound Vib.,1979, 65:151-158.
[4]Yigit A,Scott R A,Ulsoy A G.Flexural motion of a rotating beam attached to a rigid body[J].J.Sound Vib., 1988,121:201-210.
[5]Banerjee J R.Free vibration of centrifugally stiffened uniform and tapered beams using the dynamic stiffness method[J].J.Sound Vib.,2000,233:857-875.
[6]Banerjee J R,Su H,Jackson D R.Free vibration of rotating tapered beams using the dynamic stiffness method [J].J.Sound Vib.,2006,298:1034-1054.
[7]Banerjee J R.Free vibration of sandwich beams usingthe dynamic stiffness method[J].Comput Struct,2003,81: 1915-22.
[8]Chen M L,Liao Y S.Vibrations of pretwisted spinning beamsunderaxialcompressiveloadswithelastic constraints[J].J.Sound Vib.,1991,147:497-513.
[9]Wright A D,Smith G E,Thresher R W,Wang JCL.Vibration modes of centrifugally stiffened beams[J].J.Appl.Mech,1982,49:197-202.
[10]Wang G,Wereley N M.Free vibration analysis of rotatingblades with uniform tapers[J].AIAA J,2004,42: 2429-2437.
[11]Reza A,Ahmad S H.Basic displacement functions in analysis of centrifugallystiffened taperedbeams[J].Arab.J.Sci.Eng.,2011,36:841-853.
[12]吴伟浩,盛美萍,肖和业.变截面梁用于板壳耦合结构的吸振效果分析[J].噪声与振动控制,2010,5:20-24.
[13]刘见华,王晓宇,李 俊.薄壁Timoshenko梁弯扭耦合振动的动态有限元法[J].噪声与振动控制,2009,6:116-121.
Analysis of Bending Vibration of Rotating Tapered Beams Based on Finite Difference Method
ZHU You-feng1,ZHU You-guo2
(1.Shandong University of Science&Technology,Qingdao 266590,Shandong China;2.Qingdao Jiaonan Greeninvest Environmental Protection Technology Co.Ltd., Qingdao 266400,Shandong China)
The bending vibration equations of rotating tapered beams are established based on Hamilton’s principle.The equations are then discretized by using finite difference method and the mass and stiffness matrices are gotten.The natural frequencies for circular,rectangular and blade cross-section beams are obtained by using MATLAB vibration toolbox.The results of computation are analyzed and compared with those in relevant references.The linearized stationary state spaces of autonomous and non-autonomous systems are built based on the mass and stiffness matrices.Then the displacement curves and phase tracks of the rotating tapered beams are drawn with MATLAB vibration toolbox.Finally the amplitude-frequency and phase-frequency characteristic curves for the non-autonomous rotating tapered beams are plotted based on the frequency-domain analysis.
vibration and wave;taper;rotating beams;finite difference;natural frequency;state space
1006-1355(2014)03-0006-05
TK83
A
10.3969/j.issn.1006-1335.2014.03.002
旋转梁被广泛用于传动轴、风力机叶片、螺旋桨等各种旋转构件。它们产生的离心力沿几何轴线发生变化,旋转速度对刚度也有较大影响。因此,研究旋转梁的固有频率及振动特性是设计此类机械的重要基础。目前对旋转梁的研究方法主要有有限元法[1,2]、伽辽金法[3,4]、动态刚度法[5―7],另外还有假设模态法[8]和Frobenius法[9,10]。有限差分方法(FDM)是求解微分方程和偏微分方程的一种有效方法。它简单灵活,适于计算机编程运算,对梁的各种边界条件适用性好,适合处理沿几何轴线发生改变的变参数,如变截面、变化的扭转角、以及旋转梁的离心力等。本文采用有限差分离散方法,借助MATLAB振动工具箱,对几种沿水平轴旋转的垂直旋转梁进行分析,得到不同转速和锥度比的固有频率。利用状态空间分析方法对振动系统的时域特性进行了研究,得到了各种激励条件下的振动时间位移响应和相轨迹。并对非自治系统的幅频特性和相频特性研究。
2013-05-24
朱由锋(1976-),男,山东青岛人,博士研究生,讲师,从事机械振动及动力学研究。
E-mail:zhuyf1976@163.com
