移动载荷作用下斜拉桥结构的动态响应计算分析
2014-08-31袁宏智马建敏
袁宏智,马建敏
(复旦大学 力学与工程科学系,上海200433)
移动载荷作用下斜拉桥结构的动态响应计算分析
袁宏智,马建敏
(复旦大学 力学与工程科学系,上海200433)
运用斜拉桥的近似分析方法,将漂浮体系的斜拉桥结构简化成两端简支且中间离散弹性支撑梁、变地基系数梁和均匀地基系数地基梁三种模型。建立了移动载荷作用下斜拉桥结构的动力学方程,用四阶龙格库塔法对动力学方程进行了计算,对三种模型的固有频率和三种模型在相同移动载荷作用下的动态响应进行了比较,并对移动载荷移动速度、垂直振动的刚度和阻尼对桥梁动态响应的影响进行分析。结果表明,当拉索等效弹性系数较小时,三种模型的固有频率和挠度曲线差别较小,当拉索等效弹性系数较大时,三种模型的固有频率和挠度曲线差别明显;桥梁动态响应的频谱由桥梁的固有频率和移动载荷的自振频率组成;移动载荷垂直振动的刚度越大,阻尼越小,桥梁振动的响应越大。
振动与波;斜拉桥;移动载荷;动态响应
1 斜拉桥结构的简化
图1所示漂浮体系斜拉桥,按Smith[1]简化方法,忽略桥塔变形,将拉索简化成对主梁的弹性支撑。可将斜拉桥结构简化成两端简支中间离散弹性支撑梁、均匀地基系数地基梁和变地基系数地基梁三种模型。

图1 漂浮体系的斜拉桥结构
1.1 两端简支且中间离散弹性支撑梁模型
离散弹性支承梁模型中拉索等效弹性系数Ks的计算简图如图2所示,对拉索和主梁接触点施加垂直于主梁的力P使该点发生单位位移,此时拉索拉力为F,有
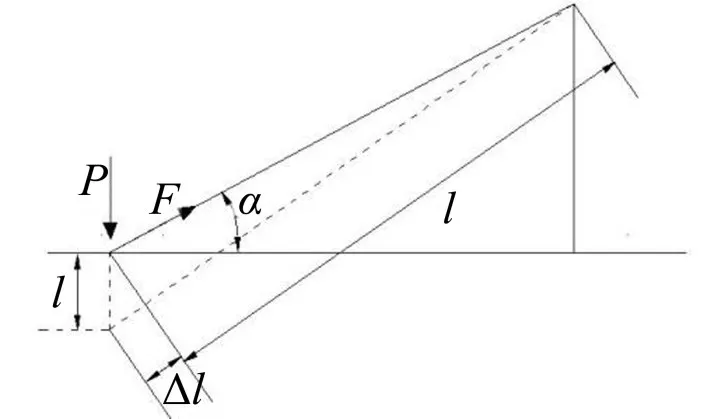
图2 拉索简化模型
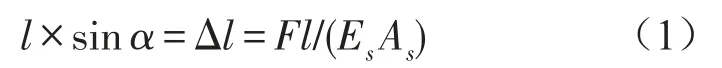
则拉索拉力的竖向分量Fy的大小等于等效弹性系数Ks,表达式如下
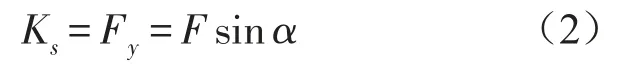
联立(1)、(2)两式,可得

其中l为拉索长度,Δl为拉索伸长量,α为拉索与梁的夹角,Es、As分别为拉索弹性模量和横截面面积,式(3)为拉索等效弹性系数表达式,按此式可得每根拉索等效弹性系数,即得离散弹性支撑梁模型,如图3。

图3 离散弹性支撑梁
1.2 均匀地基系数地基梁模型
将所有拉索等效弹性系数在主梁上均摊,得均匀的基床系数k,如下

其中Ns为拉索数量,均匀地基系数地基梁模型如图4所示
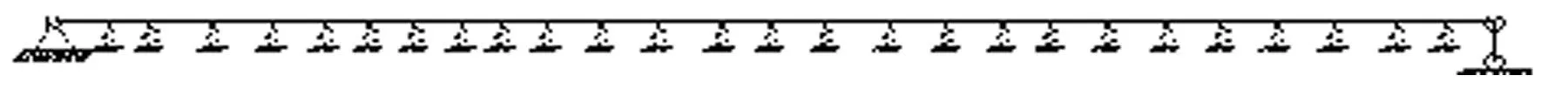
图4 均匀地基系数地基梁
1.3 变地基系数地基梁模型
由于各拉索长度不一样,式(3)算出的各拉索等效弹性系数也不一样,若直接在整根梁上均布会造成较大误差,故选取地基系数是分段变化的,处理方法如图5所示

图5 拉索分段处理示意图
设相邻两根索距为Δx,对编号为i的拉索,xi为该拉索与主梁的接触位置,Ksi为该拉索等效弹性系数,将其在区间(xi-Δx/2,xi+Δx/2)均布,即得该区间的地基系数ki=Ksi/Δx,对每根拉索进行相同处理,由于各拉索等效弹性系数不同,若索距相同,那么可得到一根变地基系数的地基梁,地基系数表达式如下

2 移动载荷作用下斜拉桥结构动力学方程的建立
为分析移动载荷作用下斜拉桥动态响应,分别用弹簧阻尼质量块和移动力模拟移动车辆载荷,如图6、图7所示

图6 移动车辆模型
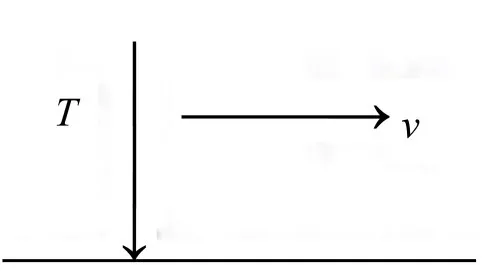
图7 移动力
2.1 移动载荷作用下离散支撑梁模型的动力学方程
忽略梁阻尼,用伽辽金法,设梁挠度函数为
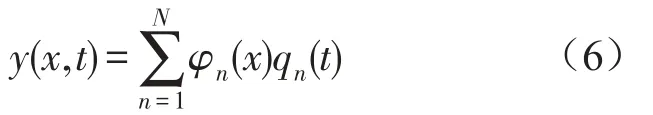
其中

为挠度函数振型,利用振型的正交性,得到移动载荷作用下离散支撑梁的振动方程如下

载荷为图6所示载荷模型时,考虑梁的振动,根据达朗贝尔原理,则载荷的动力学方程为

其中xa=xa(t)为载荷在梁上位置,z=z(t)为载荷中质量块的竖向位移。
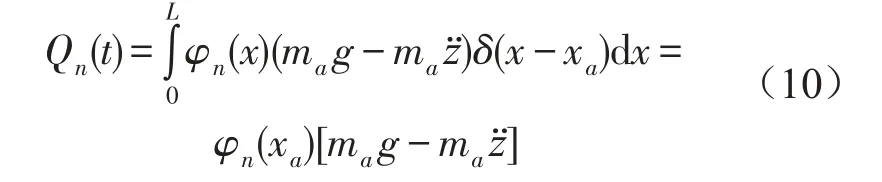
整理得

当载荷为如图7所示移动力模型时,取移动力大小为T=mag,有

将(12)式代入(8)式,得

式(11)和(13)分别表示移动车辆与移动力作用下离散支撑梁的动力学方程。
2.2 移动载荷作用下均匀地基系数地基梁的动力学方程
忽略梁阻尼,桥梁模型用均匀地基系数地基梁模型时,移动载荷作用下的梁的动力学方程为
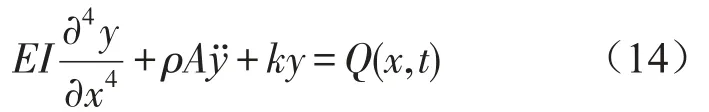
同样用伽辽金法,正交化处理得
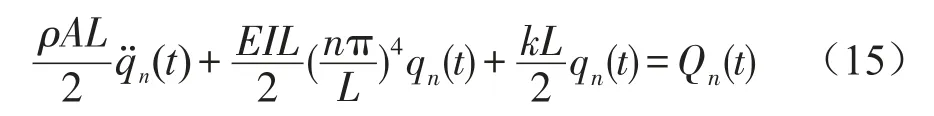
载荷为图6所示车辆模型时,Qn(t)同式(10),代入式(15)整理得

载荷为图7所示移动力时,Qn(t)同式(12),代入式(15)整理得
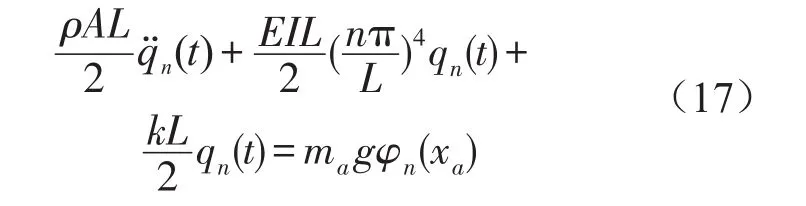
式(16)和(17)分别表示移动车辆和移动力作用下均匀地基系数地基梁动力学方程。
2.3 移动载荷作用下变地基系数地基梁模型的动力学方程
忽略梁阻尼,桥模型采用变地基系数地基梁模型,移动载荷作用下梁动力学方程为
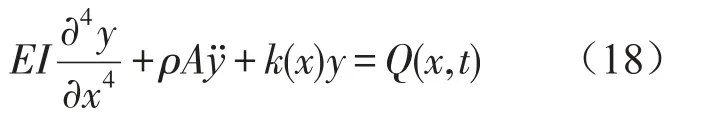
同样用伽辽金法,正交化处理得

载荷为图6所示移动车辆模型时,Qn(t)同式(10),代入式(19)整理得
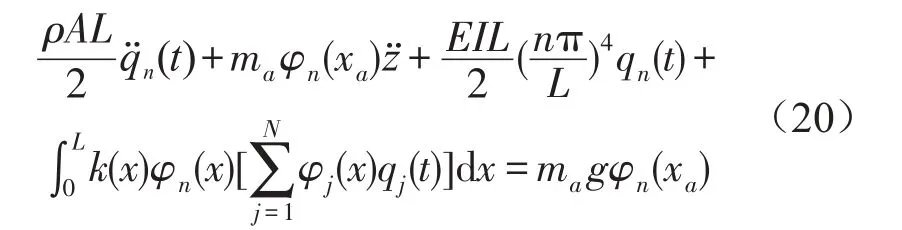
载荷为图7所示的移动力模型,Qn(t)表达式同式(12),代入式(19)整理得

式(20)和(21)分别表示移动车辆和移动力作用下变地基系数地基梁的动力学方程。
3 动力学方程的求解
3.1 离散支撑梁模型的动力学方程的求解
对于移动车辆作用下离散支撑梁的振动方程,取(6)式前N项,将(9)、(13)式整理成矩阵方程形式如下
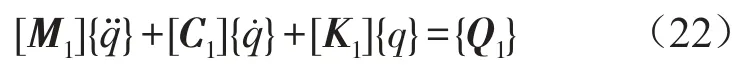
取N=3,令上述各系数矩阵表达式如下

其中
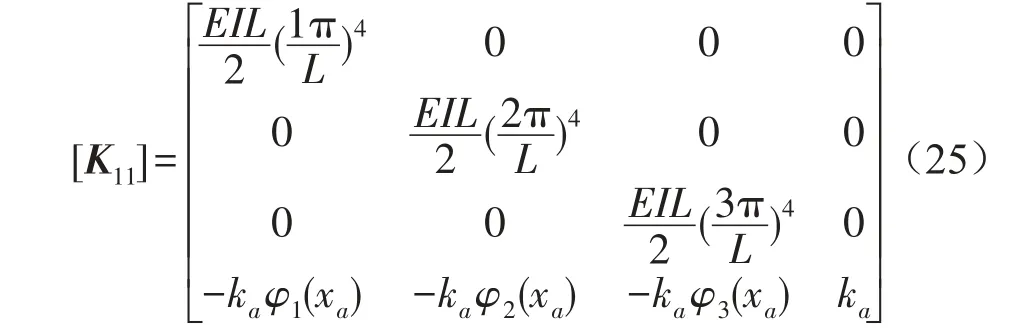

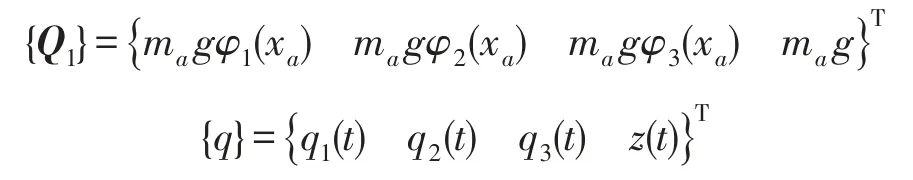
对于移动力作用下的离散支撑模型,相应的矩阵方程为
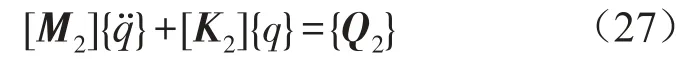
取N=3,上述各系数矩阵表达式如下
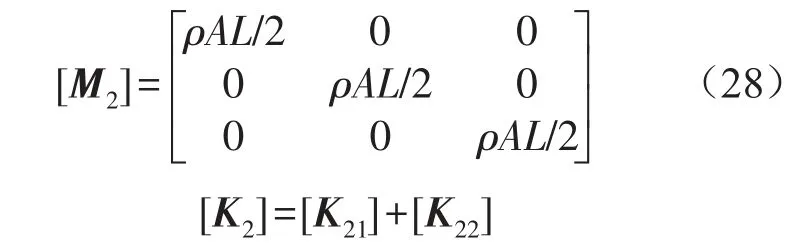
其中

3.2 均匀地基系数地基梁模型的动力学方程的求解
对于移动车辆作用下的均匀地基系数地基梁的振动方程,相应的矩阵方程为:
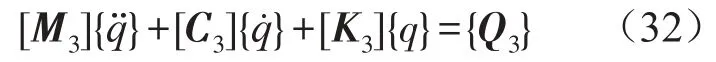
上述各系数矩阵表达式如下

其中

对于移动力作用下的均匀地基系数地基梁,相应的矩阵方程为
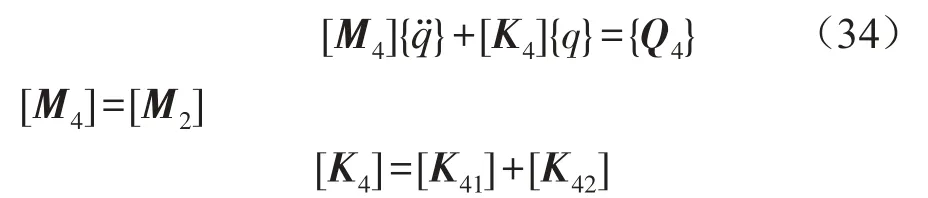
其中

3.3 变地基系数地基梁模型的动力学方程的求解
对于移动车辆作用下的变地基系数地基梁的振动方程,相应的矩阵方程为
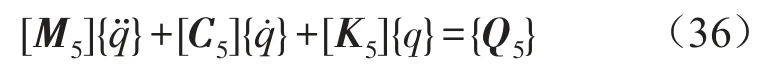
上述各系数矩阵表达式如下

其中
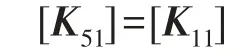

对于移动力作用下的变地基系数地基梁,相应的矩阵方程为
其中

下面将用4阶龙格库塔法求解所得矩阵方程,并对斜拉桥结构的动态响应进行频谱分析。
4 算例和结果分析
以实验室斜拉桥模型为例,梁材料45钢,密度ρ=7 800 kg/m3,长L=1.254 m,梁横截面面积、截面惯性矩和弹性模量分别为A=4.95×10-4m2、I=4.46×10-9m4和E=2.0×1011pa,移动弹簧阻尼质量系统的初始条件为z(0)=(mag/ka+0.02)m,拉索与梁夹角均为45∘,拉索数据见表1。
4.1 三种斜拉桥模型的固有频率计算
采用实验室斜拉桥模型,计算式(27)、(34)和(38),得离散支撑梁、均匀地基系数梁和变地基系数梁的第1阶固有频率分别为fd1=15.235 4 Hz、fc1=15.245 1 Hz和fv1=15.227 6 Hz。
由于实验室拉索刚度较小,三种模型的频率差别很小,现将等效弹性系数放大150倍,三种模型的第1阶固有频率则分别为和表中EsAs=4.403 8 N/m。

表1 拉索及其等效弹性系数
可以看出,当拉索等效弹性系数较小时,三种模型的第1阶固有频率差别微小,当拉索等效弹性系数较大时,三者的第1阶固有频率差别则较为明显。
用敲击法对模型第1阶频率进行测量,测得第1阶固有频率为fl=14.38 Hz,接近理论计算频率值,验证了上述理论计算的正确性,同时也说明上述简化模型是合适的。
4.2 三种桥梁模型在相同移动载荷作用下的动态响应
移动车辆载荷中取ma=0.3 kg,ka=50 N/m,ca=0,移动速度取0.2 m/s,用编制的4阶龙格库塔程序解式(22)、(32)和(36),算出三种模型在相同载荷作用下跨中挠度曲线如图8、9所示。图8所用参数为实验室模型,图9所用参数中将拉索等效弹性系数放大150倍,其他参数不变。
观察图8、9,发现在相同载荷作用下,均匀地基系数梁的跨中挠度比离散支撑梁和变地基系数梁的跨中挠度小。当拉索等效弹性系数较小时,三者跨中挠度曲线差别微小,当拉索等效弹性系数较大时,三者跨中挠度曲线的差别较明显。在实际斜拉桥中,拉索和桥梁刚度相比较大,用离散支撑梁模型和变地基系数梁模型更符合实际。
4.3 匀速移动载荷作用下斜拉桥结构的动态响应
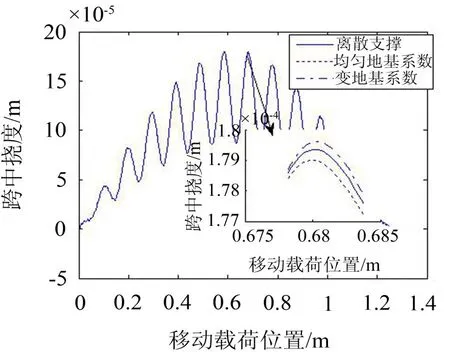
图8 跨中挠度曲线
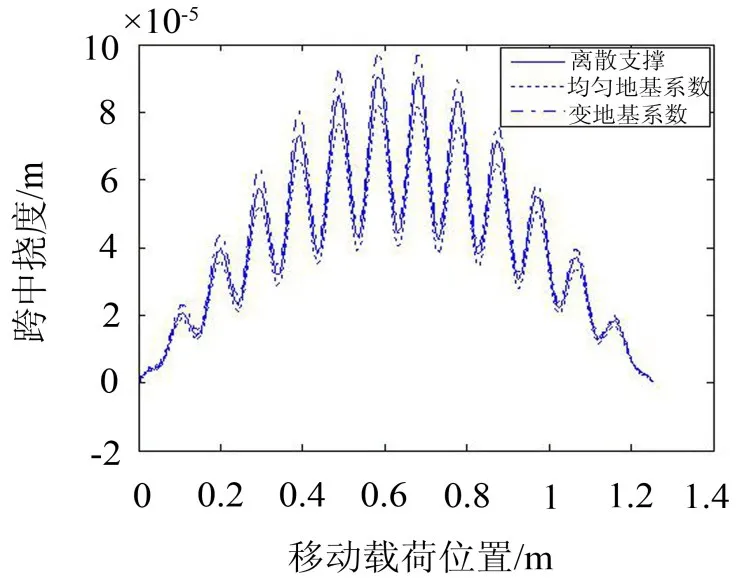
图9 跨中挠度曲线
采用变地基系数梁模型,移动车辆中取ma=0.3 kg,ka=50 N/m,ca=0,移动速度取0.6 m/ s,用编制的四阶龙格库塔程序求式(36)和(38),得移动车辆和移动力分别作用下梁的跨中挠度曲线以及频谱分析图,如图10、11所示。

图10 跨中挠度曲线
图10表明,斜拉桥结构在移动载荷作用下,跨中挠度最大值出现在载荷一端移动到另一端的中间时刻;图11频谱分析中,显示移动车辆作用下桥梁结构的动态响应比移动力作用下多一个频率,这个频率值与车辆的自振频率f1=2.054 7 Hz很接近,且均有频率f=15.2 Hz,该频率与梁固有频率15.245 1 Hz很接近,这表明移动车辆作用下斜拉桥结构动态响应的频谱由载荷自振频率和桥梁固有振动频率组成。

图11 频谱分析图
4.4 移动速度对桥梁动态响应的影响
采用变地基系数地基梁模型,移动车辆参数取ma=0.3 kg,ka=50 N/m,ca=0,移动速度取0.6 m/ s、1.0 m/s和1.4 m/s,用程序计算式(36),得梁跨中挠度曲线如下

图12 不同移动速度时跨中挠度曲线
由图12可得,移动速度增大,跨中挠度最大值变化不大,但挠度曲线上波峰数随速度的增大而减少,这是因为在相同移动载荷作用下,移动车辆的固有振动周期不变,速度越大,载荷在桥上时间就越短,移动车辆固有振动完成的周期数就越少。
4.5 移动车辆模型中弹性系数ka和阻尼系数ca对斜拉桥结构动态响应的影响
采用变地基系数地基梁模型,移动车辆参数取ma=0.3 kg,ca=0,移动速度取0.6 m/s,弹性系数取ka=50、100、150 N/m,得桥梁跨中挠度曲线如下
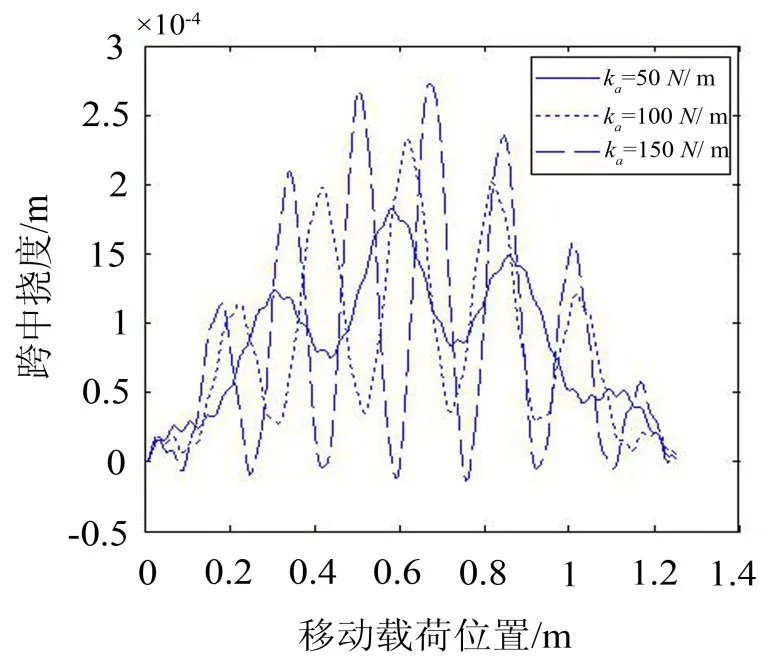
图13 不同刚度时的跨中挠度曲线
移动车辆参数取ma=0.3 kg,ka=50 N/m,移动速度取0.6 m/s,阻尼系数取ca=0、0.5、1 N·s/m,用程序求式(36),得梁跨中挠度曲线如下

图14 不同阻尼时的跨中挠度曲线
由图13、14得,移动车辆的弹性系数ka和阻尼系数ca对跨中挠度值有显著影响,ka越大,ca越小,跨中挠度最大值越大;ka越大,挠度曲线上峰值越多,这是因为ka值越大,移动车辆自振频率越高,在相同时间内,移动车辆振动完成的周期数越多。
5 结语
本文主要对移动载荷作用下斜拉桥动态响应进行了计算分析,主要结论如下:
(1)当拉索等效弹性系数较小时,离散支撑梁、均匀地基系数梁和变地基系数梁三种模型的第1阶固有频率和挠度曲线差别微小,当拉索等效弹性系数较大时,三种模型的固有频率和挠度曲线差别明显;
(2)匀速移动载荷作用下斜拉桥结构跨中挠度最大值出现在载荷从一端到另一端的中间时刻,且斜拉桥结构动态响应频谱由桥固有振动频率和移动载荷自振频率组成;
(3)移动车辆的移动速度对跨中挠度最大值影响不大,但是速度增大,挠度曲线的波峰数减少;
(4)斜拉桥在移动车辆作用下跨中挠度值受载荷中弹性系数ka和阻尼系数ca的影响,ka越大,ca越小,跨中挠度值越大;ka越大,挠度曲线上的峰数越多。
[1]Smith B S.The single plane cable stayed girder bridge:a method of analysis suitable for computer use[J].ICE Proceedings,1967,37,(1)183-194.
[2]柳惠芬.斜拉桥非线性实用简化分析[J].同济大学学报,2001,29(1):118-121.
[3]蔡四维.弹性地基梁解法[M].上海:上海科学技术出版社,1952.
[4]Kocatürk T,Simsek M.Vibration of viscoelastic beams subjected to an eccentric compressive force and a concentrated moving harmonic force[J].Journal of Sound and Vibration,291(2006),302-322.
[5]Bilello C,Paola M Di.A correction method for the analysis of continuous linear one-dimensional system under moving loads[J].Journal of Sound and Vibration, 315(2008),226-238.
[6]王颖泽.变速多移动质量耦合作用下柔性梁系统振动响应分析[J].振动与冲击,2011,30(8):56-66.
[7]周玉民,谈至明,刘伯莹.1/4车—路耦合动力学模型研究[J].同济大学学报,2012,40(3):408-413.
[8]张 庆,史家钧,胡振东.车辆—桥梁耦合作用分析[J].力学季刊,2003,24(4):577-584.
[9]张志超,赵 岩,林家浩.车桥耦合系统非平稳随机振动分析[J].振动工程学报,2007,20(5):439-446.
[10]韩万水,陈艾荣.风—汽车—桥梁系统空间耦合振动研究[J].土木工程学报,2007,40(9):53-58.
[11]楼梦麟,沈 霞.弹性地基梁振动特性的近似分析方法[J].应用力学学报,2007,21(3):149-153.
Dynamic ResponseAnalysis of Cable-stayed Bridges Subjected to Moving Load
YUAN Hong-zhi,MA Jian-min
(Department of Mechanics and Engineering Science,Fudan University,Shanghai 200433,China)
By using the approximate analysis method of cable-stayed bridge,the cable-stayed bridge of floating system is simplified into three models:a beam supported by discrete springs,a beam on an continuous elastic foundation,and a beam on an elastic continuous foundation with variable foundation coefficients.The dynamic equation of the cable-stayed bridge structure under moving load is established and solved by the forth-order Runge-Kutta method.The natural frequencies and dynamic responses of the three models are compared one another.The results show that when the equivalent elastic coefficient of the cable is small,both the difference of natural frequency and the difference of deflection of the three models are small;and when it is large,the differences are also large.The effects of velocity,stiffness and damping of the moving load on the dynamic responses of the bridge are analyzed.The results show that,the spectrum of the dynamic responses of the bridge consists of natural frequency of the bridge and the selfvibration frequency of the moving load.When the stiffness of the moving load is large or the damping is small,the responses of the bridge are great.
vibration and wave;cable-stayed bridge;moving load;dynamic responses
1006-1355(2014)03-0148-07
U441
A
10.3969/j.issn.1006-1335.2014.03.032
斜拉桥具有跨度大、重量轻、便于施工等优点,在国内外路桥建设中广泛应用。当车辆驶过桥面时,车辆移动和车辆自身振动会激起桥面振动。对此问题的研究不但有助于斜拉桥的优化设计,对斜拉桥的安全运行和寿命预测也有积极意义。
斜拉桥在移动载荷作用下动态响应的研究一直是该领域研究的重点之一,一是桥梁结构和载荷模型的简化;二是桥梁动态响应的计算分析。对桥梁结构的简化主要是拉索的简化,Smith[1]将拉索简化成对主梁的弹性支撑,并给出等效弹性系数K的表达式;柳惠芬[2]则在此基础上,将等效弹性系数在主梁上分摊,将斜拉桥简化成弹性地基梁[3]。对移动载荷的简化,Kocatürk等[4]用移动力来模拟车辆载荷,没考虑车辆载荷质量惯性和自振的影响;Bilello[5]用移动质量模拟车辆载荷,考虑了载荷质量惯性的影响;王颖泽[6]等用移动弹簧质量模拟车辆载荷;周玉民等[7]用四分之一车辆模型模拟载荷;张庆等[8]用双自由度质量弹簧阻尼来模拟载荷;张志超[9]则用两系悬挂的四轮模型来模拟车辆载荷;韩万水[10]等则用五自由度质量弹簧阻尼模拟车辆载荷三维模型。上述研究仅对简化为简支梁的桥梁进行了研究,本文将斜拉桥结构简化成两端简支中间离散弹性支撑梁、均匀地基系数梁和变地基系数梁[11]三种模型,并对三种模型的固有频率和三种模型在相同移动载荷作用下的动态响应做比较;考虑了移动载荷的水平移动和垂直振动同时对桥梁的作用,建立了斜拉桥的动力学方程,用四阶龙格库塔法对斜拉桥结构模型在移动载荷作用下的动态响应进行计算,并对移动载荷移动速度、垂直振动的刚度和阻尼对桥梁动态响应的影响进行计算分析。
2013-07-05
袁宏智(1989-),男,湖北孝感人,硕士生,目前从事土木与结构工程的研究。
E-mail:11210290015@fudan.edu.cn
