基于小波变换和陀螺的高旋弹角运动测量技术

杨登红，李东光，申强，曾广裕，杨瑞伟

(北京理工大学机电动态控制重点实验室，北京100081)

高旋弹的俯仰角速度、偏航角速度和滚转角速度的变化率低，但其滚转角速度很大，可达300 r/s，直接用陀螺难以测量如此高的角速度。本文通过对高旋弹角运动特性进行分析研究发现，以俯仰轴为敏感轴安装的低量程陀螺所敏感的角速度由俯仰、偏航和滚转角速度耦合而成，其大小主要由俯仰角速度决定，由于俯仰角速度较小，所以耦合角速度较小，因此利用低量程陀螺可以测量该耦合角速度。对该耦合角速度进行小波滤波即可获得光滑耦合角速度曲线，在短时间内，该曲线可近似为正弦曲线，利用正弦曲线过零点和极值点即可计算高旋弹的俯仰角速度、滚转角速度和滚转角。因此，本文提出一种基于小波变换和低量程陀螺的高旋弹角运动参数测量方法，利用低量程陀螺测量高旋弹耦合角速度，再利用小波变换滤波获得光滑曲线，然后利用正弦曲线过零点和极值点计算高旋弹的俯仰角速度、滚转角速度和滚转角。

1 弹体耦合角运动信号特性研究

1.1 弹体角运动耦合

采用低量程陀螺测量弹体俯仰角运动时，陀螺在弹体上的安装方式如图1所示，图中Xb、Yb、Zb轴为弹体坐标系的3个轴，弹体旋转轴为Xb轴、陀螺敏感轴为Zb、感受角速度为ωbz。

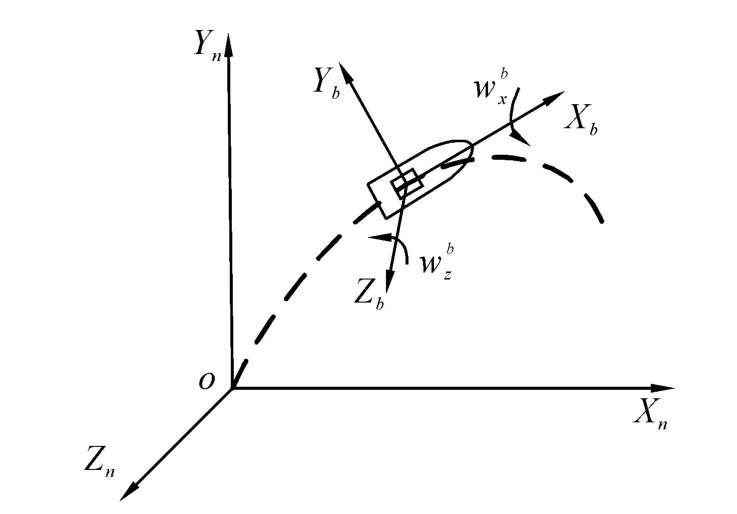
图1 低量程陀螺安装位置及敏感轴示意图Fig.1 The installation of the low-range gyro and its measurement axes

陀螺受到弹体滚转运动和偏航运动的影响，测量信号受到滚转角速度和偏航角速度调制，根据旋转弹体坐标系、非旋转弹体坐标系与地面惯性坐标转换关系可得

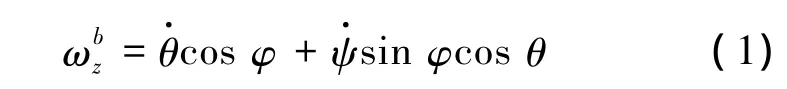
1.2 耦合参数特性

如式(1)所示低量程陀螺所测弹体角速度ωbz、受到俯仰角θ、俯仰角速度、滚转角φ和偏航角速度的影响，需要分析这些参数对耦合角速度ωbz的影响。

式(1)可根据三角函数关系改写为

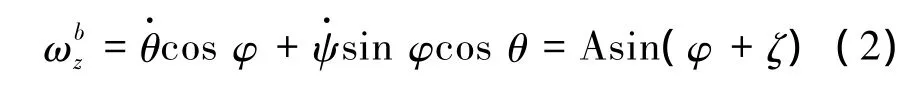
可见，在短时间内，A和φ+ζ可视为常数，则耦合角速度信号近似成以A为幅值、φ+ζ为相位的周期信号。

选取初速为900 m/s、射角为45°且随机风干扰很大的弹体角运动数据进行分析，得到结果如图2～5所示。

可见，俯仰角、偏航角和滚转角变化均比较缓慢，俯仰角速度和偏航角速度较小，且其变化率也较小，但在弹道始端和末端都有相对剧烈的变化，这些变化对小波分析有较大的影响。由图5可以看出，滚转耦合角运动变化曲线的包络变化趋势与俯仰角速度变化趋势相同，信号频率和滚转角速度相符，由局部放大图看出，耦合信号中具有明显的周期特性。

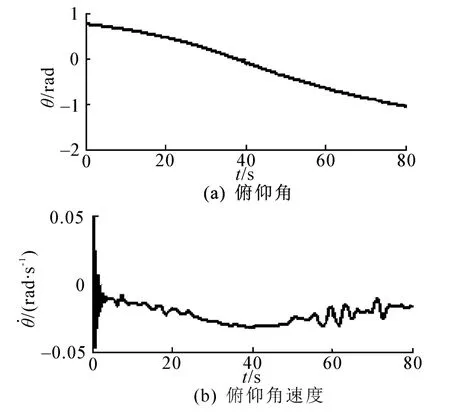
图2 俯仰角及俯仰角速度曲线Fig.2 The pitch angle and pitch rate curve

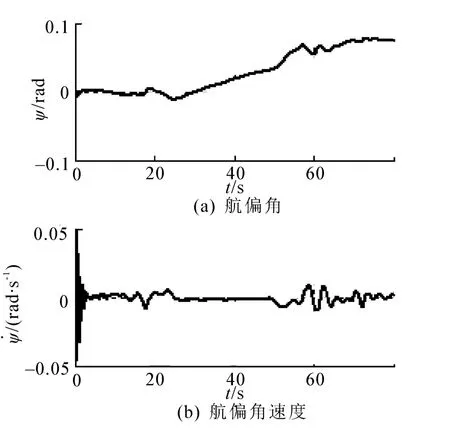
图3 偏航角及偏航角速度曲线Fig.3 The yaw angle and yaw rate curve

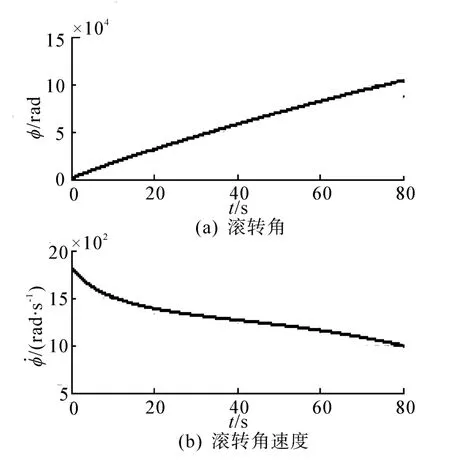
图4 滚转角及滚转角速度曲线Fig.4 The roll angle and roll rate curve

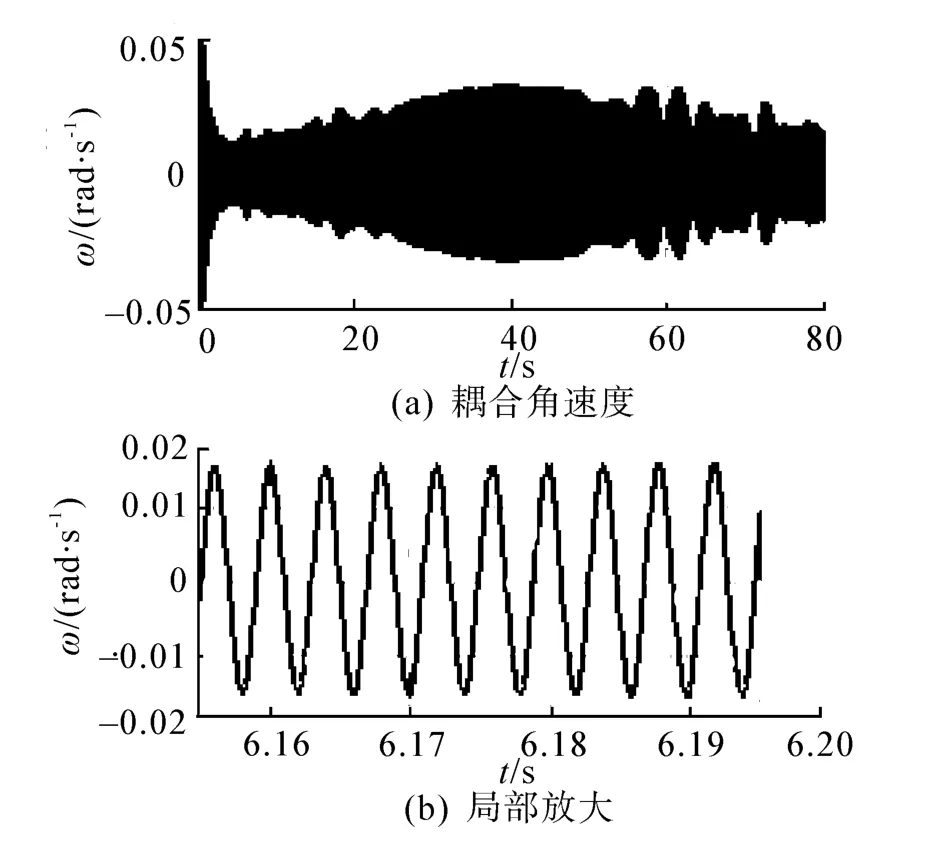
图5 耦合角速度及局部放大曲线Fig.5 The coupled angular rate and its partial curve

基于上述高旋弹耦合角速度信号的误差特性如图6所示。

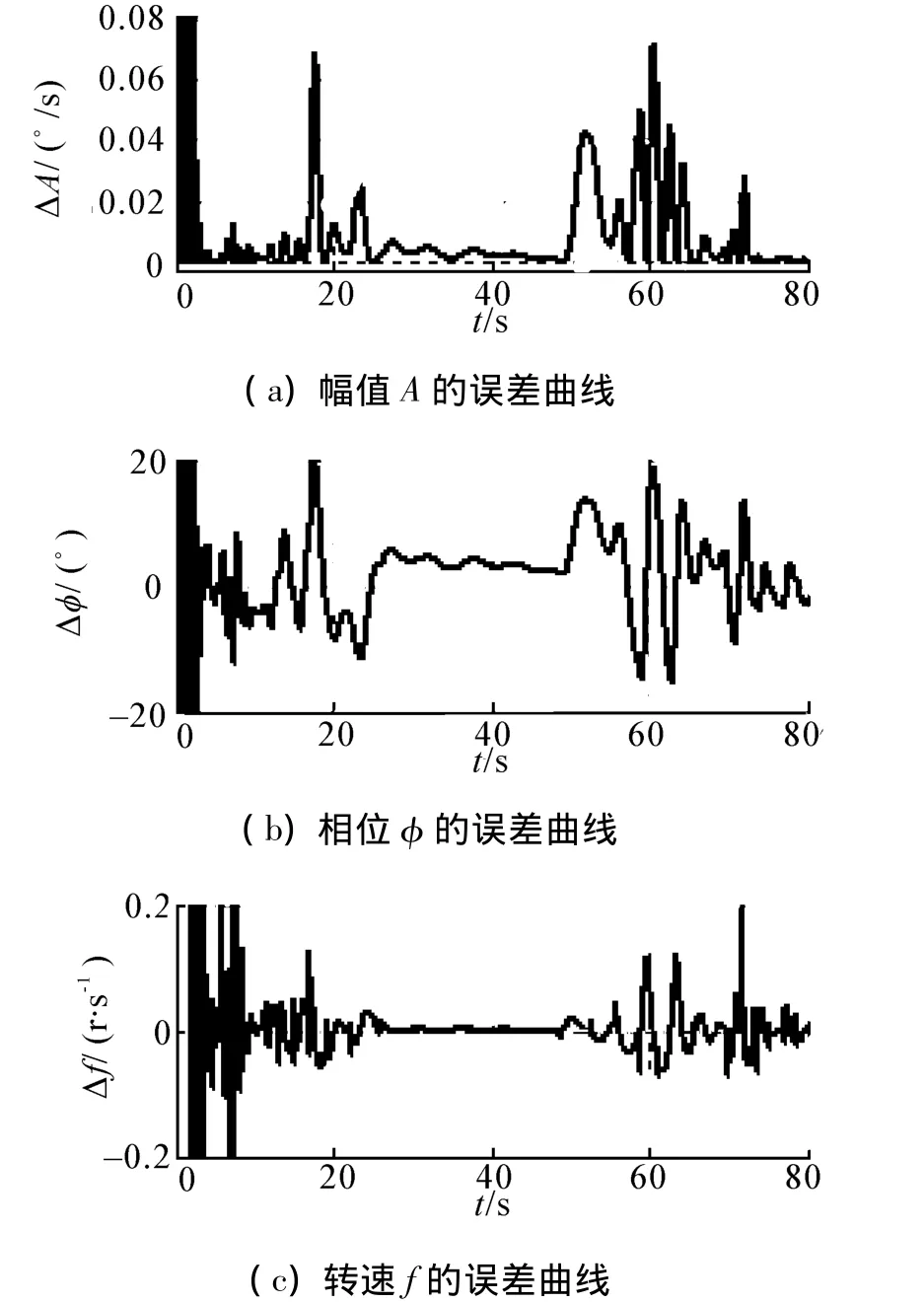
图6 耦合信号误差特性曲线Fig.6 The error characteristic curve of coupled signal

耦合信号幅值与俯仰角速度之差为 ΔA=，以幅值A作为高旋弹俯仰角速度时，其误差为 ΔA的大小如图所示，可到0.08(°)/s范围内，若对随机风进行处理，误差可以更小;由高旋弹角速度耦合产生的耦合相位为Δφ，由于随机风的干扰，该耦合相位较大，但随机风较小时，相位差值可达5°范围之内，以耦合信号相位φ+ζ作为弹体滚转角φ时，误差由Δφ即ζ决定;若以耦合角速度信号频率f=作为滚转角速度时，滚转角速度误差为Δfcos2θ)，实际误差小于 0.2r/s。可见，利用正弦曲线的过零点和极值点计算式(2)所示三角函数的幅值、相位和频率并分别作为弹体俯仰角速度、滚转角速度和滚转角φ，误差大小在上述范围内，因此采用正弦曲线的过零点和极值点计算相关角运动参数是可行的。因此本文提出的利用低量程陀螺测量耦合信号ωbz，选取合适的滤波方法对信号进行滤波处理，得到较为精确的测量值，再利用正弦曲线特性和过零相位检测法获取信号的幅值、相位及频率，从而获取弹体飞行俯仰角速度、滚转角速度和滚转角φ的角运动参数测量方法是合理的。

2 小波变换及其应用特性

小波变换由时域与时间-尺度域之间的变换和反变换组成，小波分解变换过程中，原始信号被不同尺度分解到尺度空间和小波空间，利用分解信号可将不同频带的信号进行重构，并在时域中直接观察，因此，小波变换又被称为时频特性良好的线性变换，在信号基波提取和频率测量上具有独到的优势［1-2］。若设原始信号f(t)的频段为(0～f)Hz，则原始信号的小波分解如图7(a)所示，其中，a0(k)为原始信号f(t)的采样序列f(k)，算符“↓2”表示基2的下采样，每经过一层小波分解，信号频带的尺度减半。小波分解后，可以对不同频带信号进行重构，小波重构过程如图7(b)所示。

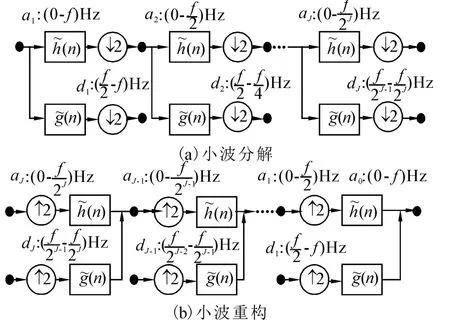
图7 小波分解与小波重构结构图Fig.7 Wavelet decomposition and wavelet reconstruction block diagram

在信号重构前，可以对某些特定的高频系数置0，可以滤除高频成分，实现信号去噪，也可以对某特定频段外的系数置0，实现信号带通或带阻滤波［2］。

小波滤波器具有线性相位特性［2］，其相位滞后与信号频率呈线性关系，实际应用中根据所设计或选用基小波的相位特性和实际信号频率对相位测量结果进行相位补偿，得到较为精确的相位测量结果。

3 高旋弹体运动参数测量方法

低量程陀螺测量弹体耦合角运动的模型如式(2)所示，可以看出耦合信号具有明显的周期特性，在短时间内具有线性的频率变化和相位变化，通过对测量信号进行小波滤波可以获取光滑的耦合角运动曲线，该曲线为近似正弦函数曲线，可分段作为正弦曲线处理。

文献［3］中采用极值法检测小波变换得到基波频率，虽然极值法原理简单，计算方便，但其对采样频率要求较高，而且非周期采样时的重构基波误差极易造成极值误差和极点漂移，影响算法测频精度。文献［4］采用过零法检测基波频率，与极值法类似，过零法的检测精度也受采样频率的影响，容易出现零点漂移。本文将过零法和极值法结合，充分利用正弦曲线过零点和极值点获取基波特征，计算出基波对应点的频率、幅值和相位。

因此，本文在利用小波滤波获取一定频带的基波的基础上，利用正弦曲线过零点和极值点计算对应点的幅值、频率和相位，并根据相关参数特性对计算结果进行平滑滤波，得到角运动耦合信号的幅值A、频率f和相位φ的测量值，对幅值、频率和相位进行一阶插值，得到幅值、频率和相位序列，再根据实测频率计算相位校正量，对相位进行校正。

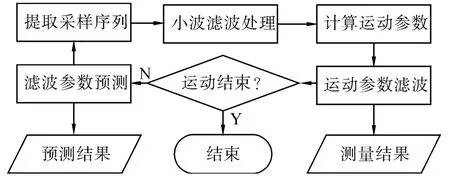
图8 角运动参数测量过程Fig.8 Angle motion parameters measuring procedure

选取初速为900 m/s、射角为45°且随机风干扰较大的弹体角运动数据采用上述角运动参数测量方法进行分析，得到结果如图9～12所示。

其中，图9为利用小波分析对耦合角运动信号滤波后得到的结果，ω为耦合角速度，Δω小波滤波滤除的干扰，可见，小波滤波有效滤除了信号中的干扰。

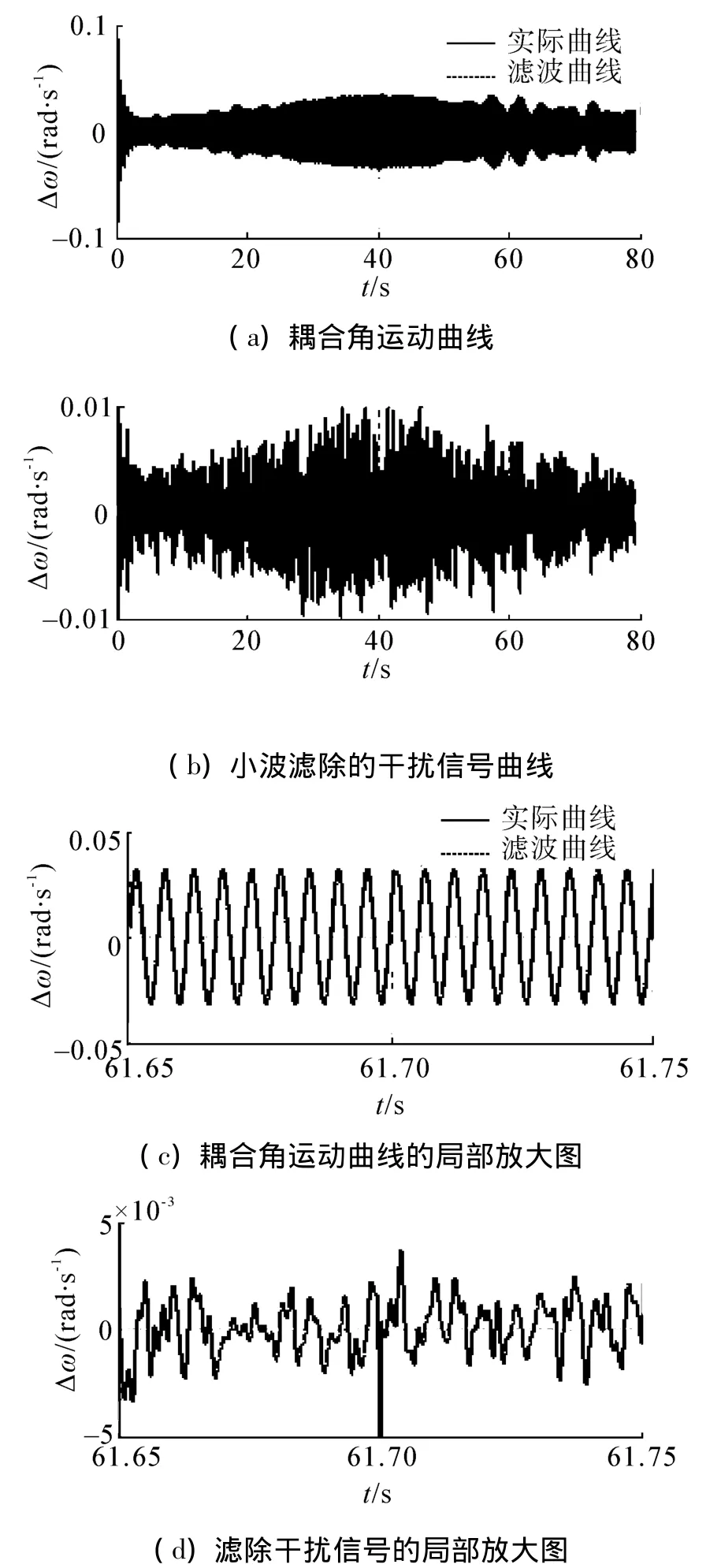
图9 角运动耦合信号和滤除噪声及局部曲线Fig.9 Coupled angular motion signal and the flitted noise with wavelet filter and its partial curve

图11为俯仰角速度测量结果及其测量误差，可见，俯仰角速度最大测量误差为1.1×10-3rad/s，即0.063(°)/s，相对精度达3.6%;图12 为滚转角测量结果及其局部放大，可见，滚转角测量误差在2°以内。

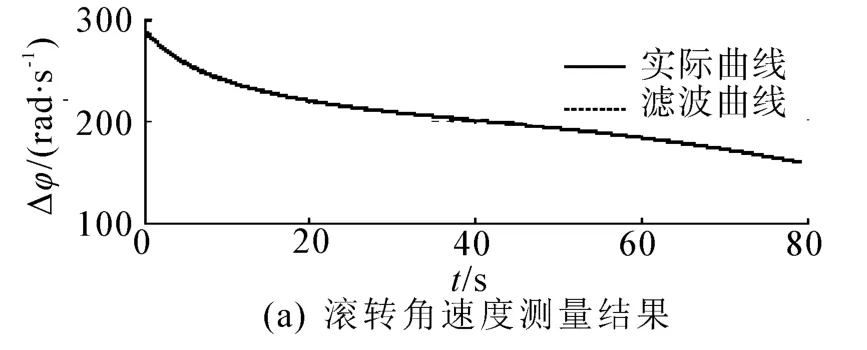
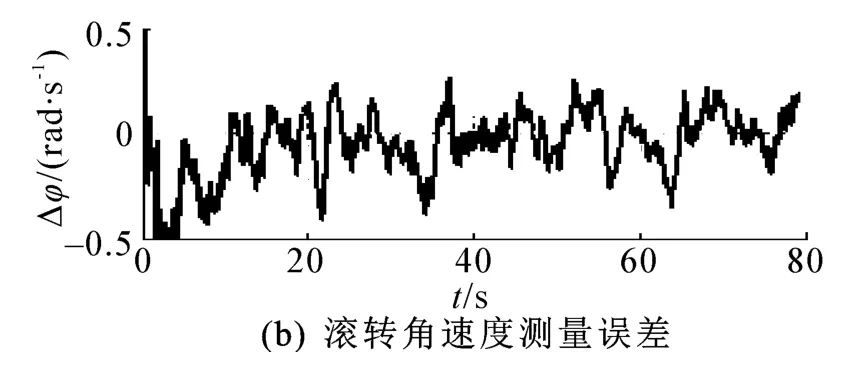
图10 转速测量结果图Fig.10 The roll rate measurement results

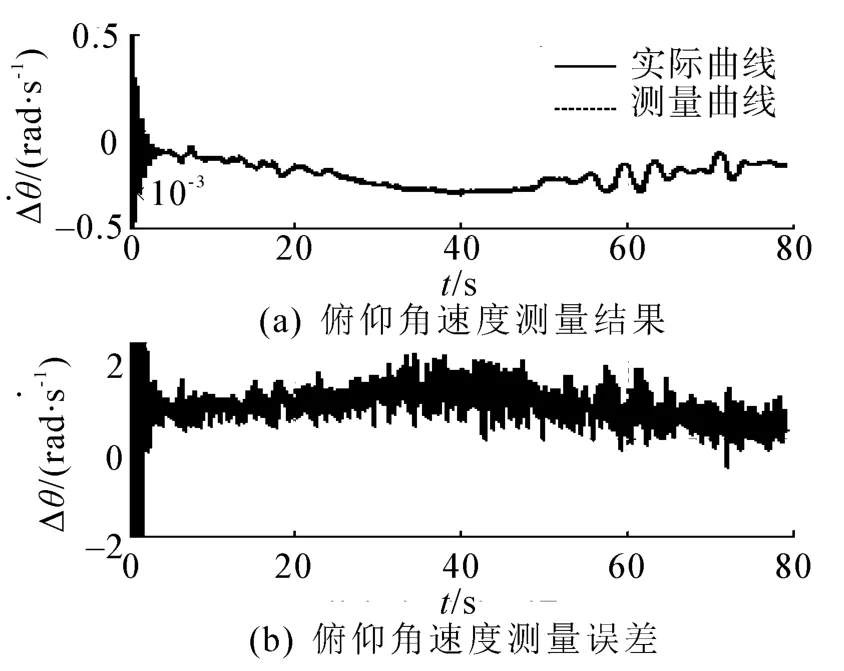
图11 俯仰角速度测量结果Fig.11 The pitch rate measurement results

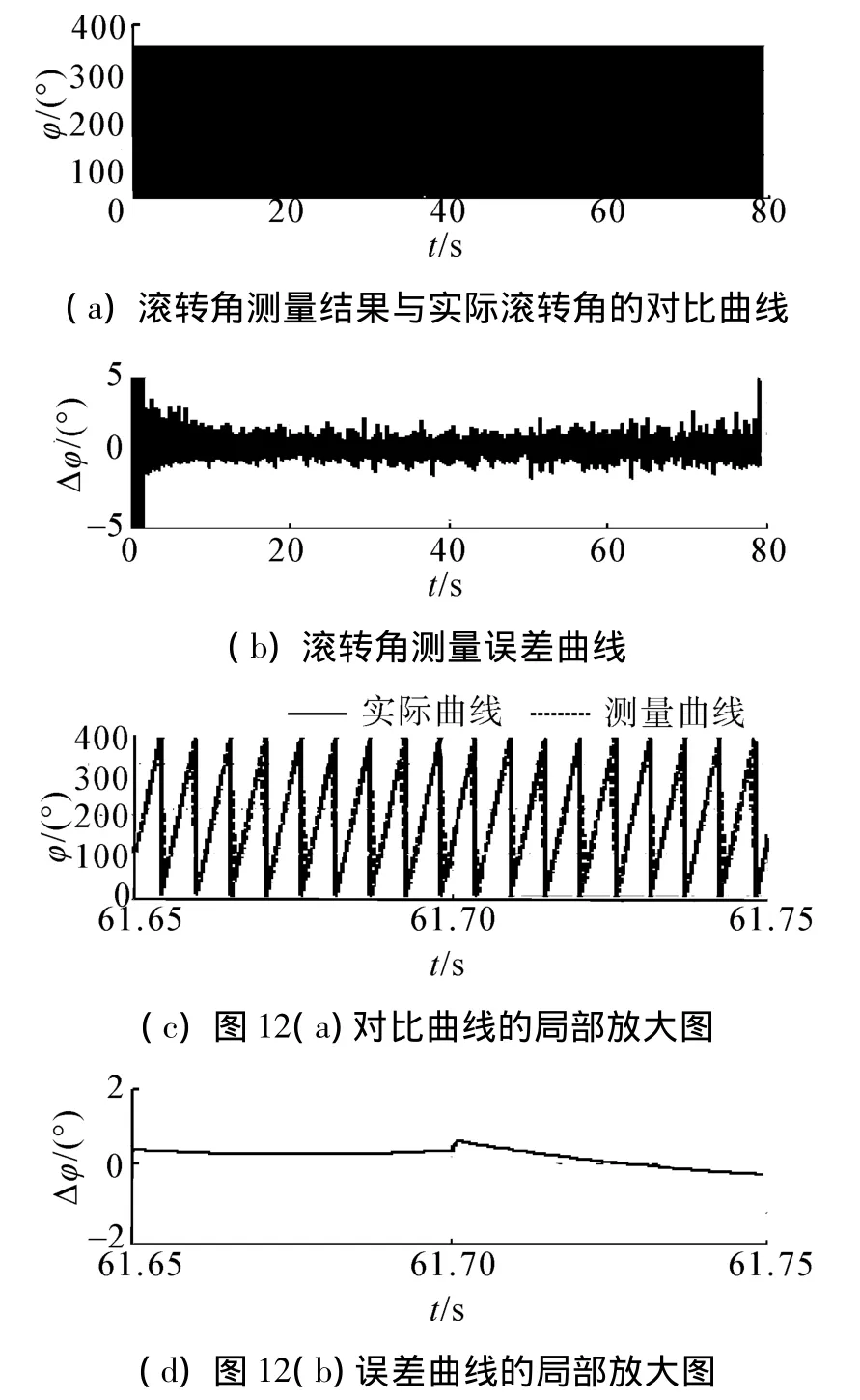
图12 相位测量结果及局部曲线Fig.12 The rotation phase measurement results and its partial curve

4 结束语

［1］应展烽，吴军基，易文俊.基于小波变换和三点法的基波频率测量［J］.电机与控制学报，2010，14(2):65-70.YING Zhanfeng，WU Junji，YI Wenjun.Study on frequency detection based on wavelet transform and three-points algorithm［J］.Electric Machines and Control，2010，14(2):65-70.

［2］范延滨，潘振宽，王正彦.小波理论算法与滤波器组［M］.北京:科学出版社，2011:50-86.FAN Yanbin，PAN Zhenkuan，WANG Zhengyan.Wavelet transform algorithm and filter bank［M］.Beijing:Science Press，2011:50-86.

［3］王肖芬，徐科军.基于小波变换的基波提取和频率测量［J］.仪器仪表学报，2005，26(2):146-151.WANG Xiaofen，XU Kejun.Fundamental wave extraction and frequency measurement based on wavelet transform［J］.Chinese Journal of Scientific Instrumentation，2005，26(2):146-151.

［4］金华烽，何奔.电力系统频率的实时估算［J］.继电器，1998，26(3):17-20.JING Huafeng，HE Ben.Real estimation of power system frequency［J］.Relay，1998，26(3):17-20.

［5］JAMES G H，CARNE T G，LAUFFER J P.The natural excitation technique(NEXT)for modal parameter extraction from operating structures［J］.Int J Anal Exp Modal Anal，1995(10):260-277.

［6］LIU K，DENG L.Experimental veri fi cation of an algorithm for identi fi cation of linear time-varying systems［J］.J Sound Vib，2004(279):1170-1180.

［7］AKYILMAZ O，KUTTERER H，SHUM C K，et al.Fuzzywavelet based prediction of Earth rotation parameters［J］.Applied Soft Computing，2011(11):837-841.

［8］MALLAT S G.A theory for multiresolution signal decomposition:the wavelet representation［J］.IEEE Trans PAMI，1989，11(7):674-693.

［9］张德丰.MATLAB小波分析［M］.北京:机械工业出版社，2009:25-215.