组合导航系统滤波器截断误差抑制方法

王延东，贾宏光(中国科学院长春光学精密机械与物理研究所，长春130033)

组合导航系统滤波器截断误差抑制方法

王延东*，贾宏光
(中国科学院长春光学精密机械与物理研究所，长春130033)

组合导航系统作为重要的定位和姿态测量的技术手段，其基本设计思想是将GPS和SINS等导航设备输出的信息经过滤波器进行最优估计。但在采用Riccati方程更新协方差矩阵和计算Kalman增益过程中，截断误差随着迭代次数的增大而累积，破坏协方差矩阵的正定性和对称性，降低滤波器计算的数值稳定性，严重时导致组合系统故障发散。本文建立了Riccati方程一阶误差模型，从理论上分析截断误差对滤波器估计性能的影响，引入基于Bierman算法和Thorton算法的Kalman滤波器进行更新方法，解决了截断误差引起的滤波器数值稳定性的问题。通过强实时半物理仿真系统验证表明，相比于基于Kalman滤波器的系统，基于Bierman-Thorton算法的组合导航系统有更强的数值稳定性和较高的导航精度。

组合导航;Bierman-Thorton算法;半物理仿真;截断误差;Kalman滤波器

GPS/SINS组合导航系统系统采用最优估计技术，使各传感器发挥各自优势，提高了系统的导航精度，降低了系统，广泛应用于地面车辆、航空、航天和航海等领域。组合导航系统中，由于各状态变量及其初始对准估计误差的数值范围较大，导致其协方差矩阵通常为病态矩阵，而截断误差作为较小的扰动极易破坏其数值稳定性，甚至造成滤波器发散。并且组合导航系统滤波器、矩阵维数大、反复的矩阵乘法和求逆运算，都会引起较大的截断误差。因此在组合导航系统中减小截断误差就非常重要。

组合导航系统中无论采用线性Kalman滤波器，还是EKF等非线性滤波器，都须对Riccati方程进行迭代运算［1］，本文探讨了Riccati方程更新过程中的共性问题。前人针对以上问题提出了许多数值计算方法，如Swerling求逆公式，Potter求逆算法，Joseph稳定算法，信息滤波器，Calson-Schmidt平方根算法和Bierman-Thorton算法，参见文献［1］。本文对比了截断误差引起的协方差矩阵误差的均方根，说明了基于UD分解的Bierman-Thorton量测更新和时间更新算法，对减小舍入误差引起的数值计算不稳定，抑制系统发散，减小计算量有明显的作用。并以某制导武器组合导航系统进行半物理仿真，分析Bierman-Thorton算法的在抑制滤波器抑制截断误差的作用［2］。

1 组合导航系统算法

组合导航系统的本质是应用信息融合技术，特别是滤波技术，对多传感器输出的信息量进行最优估计的过程。在组合导航系统的设计过程中，首先建立组合导航系统的状态方程和量测方程;采用Kalman等滤波器对系统状态进行最优估计，从噪声中估计出状态变量的最优值;利用这些状态估计值修正系统误差，进而得到准确的导航状态，达到提高定位和测姿精度的目的。

1.1 组合导航模型

本文的组合导航系统采用SINS误差量和惯性器件误差量作为状态变量，为了使系统方程为线性方程，SINS误差忽略了二阶及以上的误差小量，参见文献［3］。惯性器件应先根据惯性器件模型进行标定，补偿大部分的系统误差，而后对随机误差进行辨识和建模。组合导航系统原理，见图1［3-4］。

图1 组合导航系统原理图

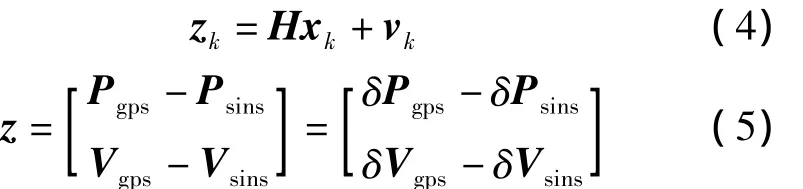
1.2 组合导航系统Kalman滤波计算方法

卡尔曼滤波器的实质是基于最小方差的估计算法，利用确定性和随机性的先验信息，通过初始值不

由以上分析，组合导航系统状态向量为:

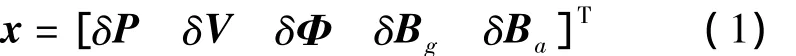
其中:δP表示当地地理下的位置误差，分别为纬度误差、经度误差和高度误差;δV表示当地地理坐标系下的三轴速度误差;δΦ表示载体系相对于当地地理坐标系的误差角;δBg表示三轴陀螺的零偏; δBa表示三轴加速度计的零偏。

则组合导航连续系统的状态方程为:其中:F为组合导航系统状态矩阵;G为噪声驱动矩阵;w为系统噪声。

系统噪声w由陀螺零偏稳定性wgb和白噪声wgr、加速度计零偏稳定性wab和白噪声war组成，见式(3)。

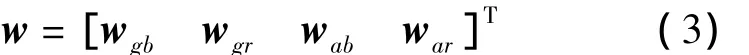
系统的量测方程为式(4)，量测值为GPS与SINS二者输出的速度位置之差，见式(5)。断的递推，得出最小方差的估计值。卡尔曼滤波器5个要素包含:式(1)状态方程;式(6)系统噪声方差矩阵;式(8)协方差矩阵;式(5)量测方程;式(8)量测噪声方差矩阵。

Riccati方程的迭代计算完成的是协方差矩阵P和Kalman增益K的更新，见式(9)～(11)。式(9)为协方差矩阵的时间更新，式(10)为Kalman增益的计算，式(11)为协方差矩阵的量测更新［5］。

在完成P的更新和K计算后，计算组合导航系统误差修正量，闭环修正系统误差修正量见式(13)，并以此校正SINS解算值和陀螺输出值，见式(13)。

1 截断误差对组合导航系统卡尔曼滤波器的影响

2.1 病态矩阵和矩阵的条件数

在数值计算中，当矩阵为“病态”时，数据存在微小扰动(误差)时，引起的输出数据(问题解)相对误差很大，该矩阵即为病态矩阵。矩阵病态特性以矩阵的条件数表示。

设A为非奇异阵，cond(A)υ为矩阵的条件数，见式(14)。

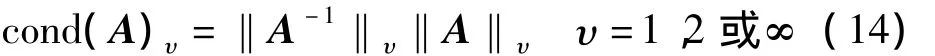
根据定义可知cond(A)≥1;当状态数值cond(A)接近∞时，A为奇异矩阵。cond(A)越接近于1，状态越好［4］。

2.2 截断误差对卡尔曼滤波器的影响

理论上在Kalman滤波中，Riccati方程协方差矩阵应与实际系统估计不确定性相同，如果二者存在差异，则认为存在“病态”问题。但是，在组合导航系统工程实现中存在许多问题可能引起协方差矩阵的“病态”。具体地说，①当建模不准确时，特别是对于采用系统误差量作为状态变量时(忽略了二阶小量)，导致理论模型与实际系统存在差异;②当滤波器选取的状态变量的方差估计值的数值范围相差较大;③式(16)中矩阵［HPHT+R］求逆计算;④数值计算的截断误差;⑤矩阵维数过大;⑥处理器的计算精度较低等。这些情况中，一些是不能解决的，一些是能够避免的。例如对惯性器件进行精密的标定，采用导航输出值作为状态变量并采用非线性滤波器进行估计能够一定程度地避免建模不准确的问题;矩阵求逆和大维数问题通过将稀疏矩阵分块计算，向量计算转化为标量的序贯处理方法解决;截断误差可采用对正定对称的协方差矩阵进行分解，并对分解后的三角矩阵和对角矩阵分别进行更新的方法克服［6］。例如，将P进行Cholesky分解，见式(15)，对矩阵C进行更新计算，这个思想即为平方根滤波器的基本思想。

考虑截断误差在Kalman滤波器传播方式，见式(9)。协方差矩阵P的一阶传播模型可写成式(16)。其中，δ项表示为累积误差，Δ表示为本次迭代引入的截断误差，f1为δPk(-)的一阶函数。

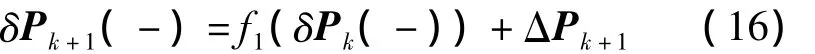
经过量测更新后的δPk+1(+)为式(17)。

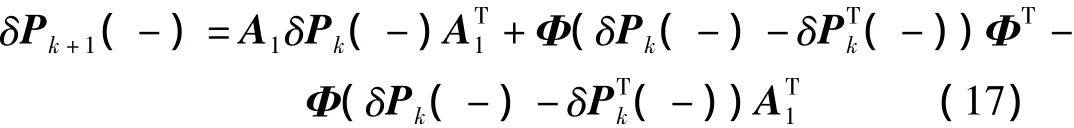
其中，A1=Φ-KkH。

平方根滤波器对P进行Cholesky，将分解后的矩阵进行量测更新和时间更新。平方根滤波器的截断误差一阶传播过程见式(18)。

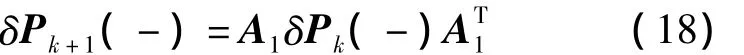
通过与式(17)对比看出，式(24)减少了对称性误差Φ(δPk(-)-δ(-))ΦT和非对称误差Φ (δPk(-)-δ(-)的引入。

不同的Kalman滤波器数值计算方法中的截断误差对协方差矩阵估计精度的影响不同，见图2。从图2中看出，Bierman与Calson量测更新算法在截断误差为小数点后9位时仍能得到较高的计算精度。

式(18)与式(17)相比说明平方根滤波器在抑

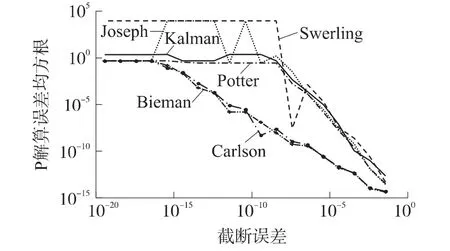
图2 Kalman滤波量测更新算法截断误差对协方差矩阵的影响

3 Bierman-Thorton算法基本原理

制截断误差在Riccati方程中传播具有明显的优势。基于改进Cholesky分解的量测更新和时间更新方法的称为改进的平方根滤波器或称为UD滤波器［7-8］。

3.1 改进Cholesky分解

对于一个正定对称矩阵能够分解为成式(19)的形式，其中U为上三角矩阵，D为对角矩阵，矩阵对角线元素为非零值。

3.2 过程噪声方差矩阵的对角化

在Thorton-Bierman算法中，须对过程噪声进行对角化处理。对角化方法即为改进Cholesky分解，见式(20)。

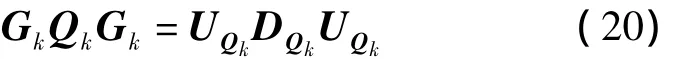
3.3 Bierman量测更新

Bierman算法完成的Riccati方程的量测更新，利用序贯处理的基本思想，设h为量测矩阵H的任意一维行向量，r为量测噪声R的对角元素，则协方差矩阵本次更新见式(21)和式(22)［9］。

3.4 Thorton时间更新

Thorton算法完成的是协方差矩阵的时间更新，Thorton时间更新算法也称作改进的加权Gram-Schmidt(MWGS)算法，相较于标准Gram-Schmidt算法有更强的数值稳定性。按照式(29)对系统噪声矩阵GkQkGk进行对角化处理，并定义矩阵A和Dw，见式(23)和式(24)。

采用加权Gram-Schmit正交化的思想，对A进行分解:

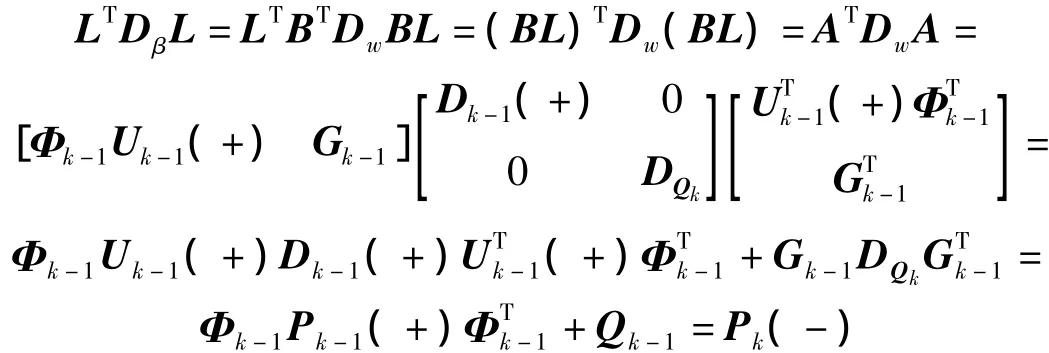
则LT和Dβ为时间更新后的上三角矩阵和对角矩阵，见(25)～(26)。

根据以上分析，基于Bierman-Thorton算法的组合导航系统设计过程见图3。

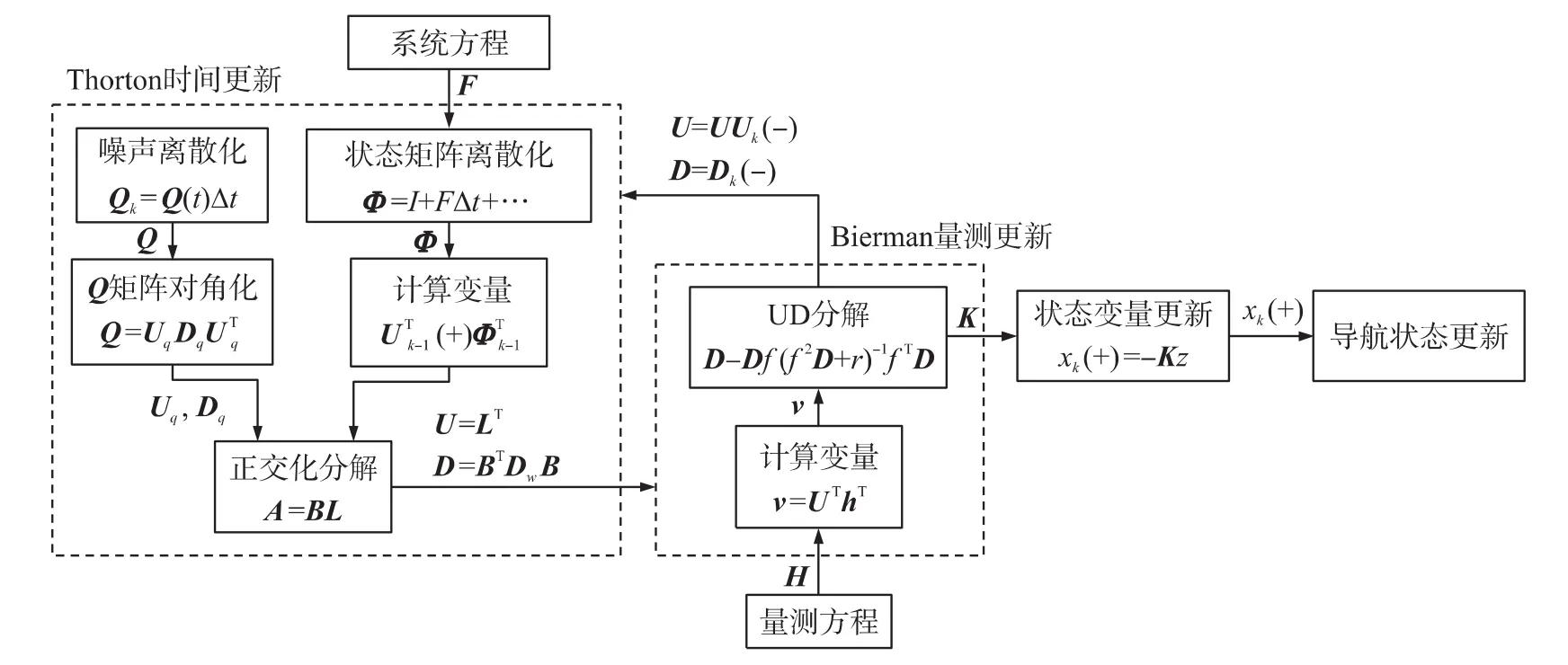
图3 UD滤波器组合导航系统原理图

4 组合导航系统半物理仿真

4.1半物理仿真系统

组合导航半物理仿真原理如图4所示。半物理仿真也称硬件在回路仿真，通过仿真机生成数字弹道，作用于仿真设备，仿真设备按照输入为被测对象提供物理效应，被测对象通过其上的传感器感知物理效应，按照设计的算法输出仿真结果［8］。

图4 组合导航半物理仿真原理图

组合导航系统半物理仿真系统由轨迹仿真机、三轴转台、GPS模拟器组成和数据显示和记录计算机组成。为保证仿真的强实时性，在VxWorks实时系统下开发，运行轨迹生成器，通过光纤反射内存与三轴仿真转台进行通信，通信内容为当前角位置;组合导航系统中的三轴陀螺固联安装在仿真转台上，输出角速度至导航计算机;仿真机根据加速度计标定后的误差模型，通过422串口按照加速度计协议将比力发送至导航计算机;仿真机计算当前地球坐标系的位置、速度、加速度、角位置、角速度和角加速度通过TCP/IP协议发送至GPS模拟器，GPS模拟器根据以上信息计算当前位置和时间计算生成GPS卫星的射频信号，将射频信号输入至组合导航系统中GPS接收机的接收端，GPS接收机将解算的位置和速度发送至导航计算机，完成组合导航计算，参见文献［10-11］。

根据Bierman-Thorton算法，在嵌入式系统中进行工程实现。嵌入式处理器采用TI公司的TMS320F28335浮点处理器，陀螺选择美国AD公司生产的ADIS16136三轴MEMS陀螺，性能指标见表1;加速度计选择COLBRYS公司生产的MEMS加速度计MS8000-10加速度计，性能指标见表2;GNSS接收机选择东方联星公司生产的CNS50 GPS接收机，性能指标见表3，参加文献［12-13］。

表1 ADIS16136陀螺关键指标

表2 MS9000-50加速度计关键指标

表3 CNS50 GPS接收机关键指标

4.2半物理仿真结果

根据以上基于Bierman-Thorton的组合导航系统算法，对其进行工程实现，并进行半物理仿真，仿真结果见图5～图8和表4。

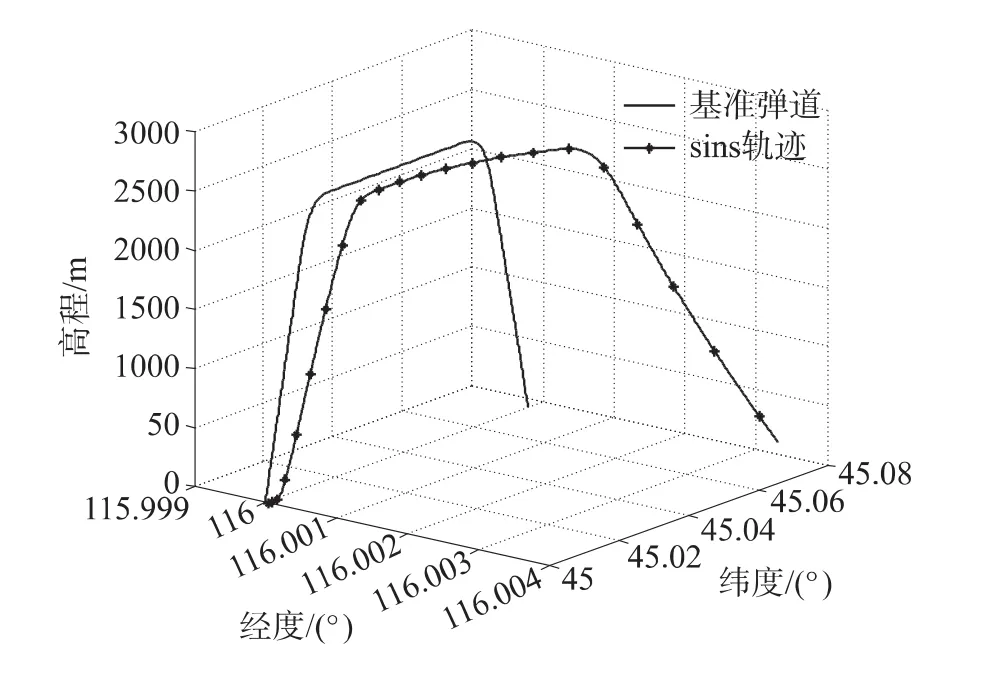
图5 仿真基准弹道

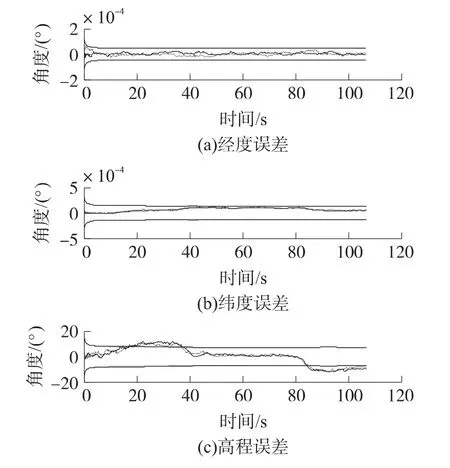
图6 位置误差

图7 速度误差

图8 姿态角误差

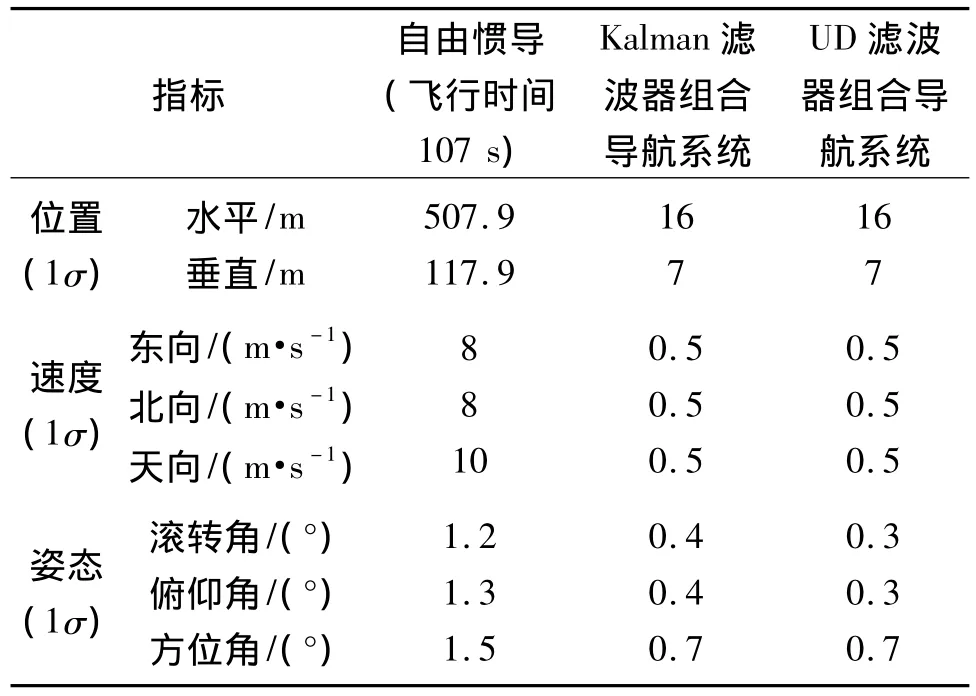
表4 自由惯导系统、Kalman滤波器和改进平方根滤波器半物理仿真结果对比

从仿真结果看出，相对于自由惯导系统，组合导航系统精度明显提高。改进平方根滤波器与传统Kalman滤波器相比，由于截断误差影响较小，姿态解算精度优于Kalman滤波器。位置和速度的解算精度相当。

根据式(20)，对比Kalman滤波器和改进平方根滤波器的协方差矩阵的条件数，取矩阵的∞范数，见图9。由于状态变量之间的估计误差差异较大，协方差矩阵都为病态矩阵，但结果表明，基于改进平方根滤波器的条件数小于Kalman滤波器一个量级，说明基于改进平方根滤波器数值稳定性优越。

图9 改进平方根滤波器与Kalman滤波器组合导航系统协方差矩阵条件数

5 结论

本文介绍了组合导航系统的设计方法，论证了截断误差在Kalman滤波器Riccati方程迭代运算中的传播的方式;并提出了抑制截断误差的方法，即Bierman-Thorton量测更新和时间更新算法。通过半物理仿真验证，基于改进平方根滤波器的组合导航系统具有数值稳定性强，导航精度高的优势。文中对截断误差对导航精度和可靠性进行了系统分析，但对于组合导航系统，影响其精度和可靠性的误差源还包括粗大误差，传感器测量野值等重要因素，这些因此也能够以适当数值算法克服，因此在解决截断误差的组合导航系统的同时，也需深入研究粗大误差，传感器测量野值等误差机理和解决方法。

［1］Brown R G，Hwang P Y C.Introduction to Random Signals and Applied Kalman Filtering［M］.2nd Ed.New York:Wiley，1992:156 -162

［2］Verhaegen M，Van Dooren P.Numerical Aspects of Different Kalman Filter Implementations［J］.IEEE Transactions on Automatic Control，1986(31):907-917

［3］Rogers R M.Applied Mathematics in Integrated Navigation Systems［M］.3rd Ed.New York:American Institute of Aeronautics and Astronautics，Inc.，2007:267-277

［4］马骏，杨功流.紧耦合MINS/GPS组合导航系统数据融合的分析与处理［J］.传感技术学报，2011，24(9):1284-1289

［5］Gibbs，Richard G.Square Root Modified Bryson-Frazier Smoother［J］. IEEE Transactions on Automatic Control，2011，56(2)，452-456.

［6］Grewal M S，Andrews A P.Kalman Filtering Theory and Practice U-sing MATLAB［M］.New York:Wiley，2008:238-242

［7］Richard G Gibbs.New Kalman Filter and Smoother Consistency Tests［J］.Automatica，2013，49:3141-3144.

［8］Michael K T，Jeffrey L A，Craig H B.Ensemble Square Root Filters［J］.Notes and Correspondence，2002，25(6):862-863.

［9］白亮，秦永元，成研.基于序贯处理的航位推算组合导航算法研究［J］.传感技术学报，2010，23(5):687-690.

［10］方靖，顾启泰，刘学斌，等.MINS/GPS组合导航系统设计与实验［J］.清华大学学报(自然科学版)，2007，47(8):1316-1319.

［11］隋树林，袁健，张文霞，等.基于UD-EKF自主光学导航方法仿真［J］.系统仿真学报，2007，19(3):482-485.

［12］Liu Guangfu，Zhang Weigong，Liu Xu，et al.Data Synchronization in IMU/GPS Integrated Measurement System of Vehicle Motion Parameters［J］.Journal of Southeast University(English Edition)，2006，22(2):200-203.

［13］高宪军，翟林培.GPS/INS组合导航系统的研究［J］.光学精密工程，2004，12(2):146-149.

王延东(1985-)，男，辽宁本溪人，毕业于北京理工大学。助理研究员，硕士，主要从事组合导航技术和半物理仿真研究，wyd321@126.com;

贾宏光(1971-)，男，黑龙江五常人，毕业于中科院长春光机所。研究员，博士生导师，主要从事飞行器总体设计。

Roundoff Error Restraining Method of Integrated Navigation System

WANG Yandong*，JIA Hongguang

(Changchun Institute of Optics，Fine Mechanics and Physics，Chinese Academy of Sciences，Changchun 130033，China)

As the most important technology for positioning and attitude measuring，the integrated navigation system is made use of SINS and GPS information for optimal estimation by Kalman filtering.It is reviewed that the roundoff error accumulating would undermine the numerical stability of the filter，when the estimation covariance matrix is updated by virtue of Riccati equation.Severely，it ruined the property of positive-definite of covariance matrix，leading the navigation system to divergence.It is presented the one order model of roundoff error propagation of Riccati equation，and analyzed how roundoff error affect Kalman filtering in theory.It is introduced the Bierman-Thorton algorithm in the essay，and the element of the algorithm is described to how to solve the numerical stability problem due to roundoff error in integrated navigation system.Consequently，it is proved that Riccati equation updating by Bierman-Thorton algorithm has better numerical stability and accuracy than which by conventional Kalman filtering，which is borne on hardware-in-the-loop simulation.

integrated navigation system;Bierman-Thorton algorithm;hardware-in-the-loop simulation;roundoff error;Kalman filtering

V249.3

A

1004－1699(2014)05－0616－06

10.3969/j.issn.1004－1699.2014.05.009

2014-01-16

2014-04-16