基于相关向量机的MEMS陀螺仪随机漂移补偿

沈强，刘洁瑜，王琪，王杰飞(第二炮兵工程大学，西安710025)

基于相关向量机的MEMS陀螺仪随机漂移补偿

沈强，刘洁瑜*，王琪，王杰飞
(第二炮兵工程大学，西安710025)

提出了一种基于相关向量机的MEMS陀螺仪随机漂移预测方法。针对MEMS陀螺仪随机漂移误差的非线性、不确定性等特点，建立了相关向量机预测模型，并采用EM算法获得模型的参数。针对随机漂移的混沌特性，利用相空间重构技术，将重构后的漂移序列作为输入变量进行模型的训练和预测。训练和测试结果均表明，该方法具有很好的预测效果，优于常用的时间序列分析法和支持向量机法。利用预测结果对随机漂移进行补偿，有效地提高了陀螺的使用精度。

MEMS陀螺仪;随机漂移;相关向量机;相空间重构;EM算法

随着精确制导武器的迅速发展，MEMS惯性器件正成为当前惯性技术的一个研究热点。MEMS陀螺的随机漂移产生的机理错综复杂，具有非线性和不确定性等特点，已成为影响MEMS陀螺仪精度的主要因素，必须通过有效的方法进行预测和补偿［1］。

比较常用的处理方法包括以时间序列分析为主的线性预测方法和神经网络、机器学习等非线性预测方法。文献［2-4］将线性预测方法和神经网络应用于MEMS陀螺的随机漂移补偿，在一定程度上提高了陀螺仪的精度，但是线性预测方法必须假设时间序列具有平稳性、独立性特征，会对模型的精度产生不利影响;神经网络存在过拟合现象，算法泛化能力差。基于机器学习理论的支持向量机方法SVM(Support Vector Machine)不易发生过拟合现象，有良好的泛化性能，文献［5-6］将SVM用于陀螺仪随机误差的建模，取得了较好的效果。但该方法也具有明显的缺陷:解相对上述方法是稀疏的，但当训练集增大时，核函数数量显著增加;需要调整不敏感参数，通常要求交叉验证，浪费时间和数据计算;核函数必须为连续对称的正定核。

相关向量机RVM(Relevance Vector Machine)是一种新的机器学习算法，与SVM相比，它是一种基于贝叶斯的稀疏概率模型，通过回归估计获得预测值的分布。RVM能够突破SVM固有的局限，在预测性能相当的情况下，能够极大的减少所需的核函数［7-8］。

本文将相关向量机用于MEMS陀螺仪的随机漂移预测补偿。首先对随机漂移序列进行相空间重构，然后利用重构后的时间序列建立RVM预测模型，并采用EM算法估计模型参数，最后通过实验验证模型的有效性。

1 相关向量机模型

假定训练样本集{xi，ti}ni=1，目标值ti独立分布，且带有附加噪声εi，则目标值可以表示为

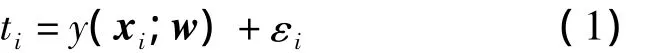
其中，w是模型权值。则RVM的模型由下式定义［9］

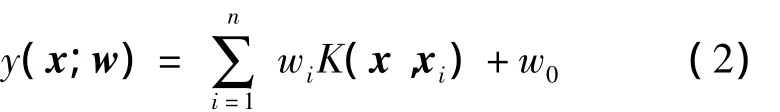
式中，w=(w0，w1，…，wn)T为权值，K(·，·)为核函数，基函数由核参数化。

假设εi～N(0，σ2)，σ2假设为未知量，后面在数据训练的时候迭代更新获取。则存在p(ti|x)=N(ti|y(xi)，σ2)。那么数据集的似然函数可以表示为

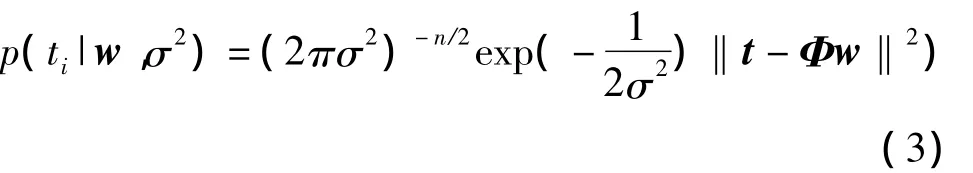
其中，t=(t1，t2，…，tn)T为目标向量;Φ=［φ(x1)，φ(x2)，…，φ(xn)］T为参数向量;φ(xi)=［1，K (x1，xi)，…，K(xn，xi)］T为基函数。

如果直接通过最大似然函数来估计w，会导致过学习现象，因而定义服从高斯分布的先验概率分布

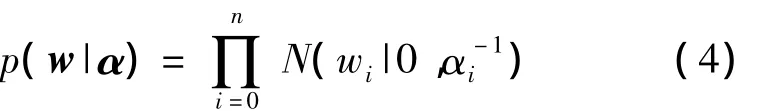
α=(α0，α1，…，αn)T为n+1维超参数。这样每一个权值对应一个独立的超参数，这是导致模型稀疏性的根本原因。

2 MEMS陀螺随机漂移建模

MEMS陀螺随机漂移可以看成是一个与温度、形变、应力干扰等相关量有关的多维非线性混沌系统。受各种变量的影响，随机漂移具有相对复杂、难以精确预测的特点。一般的建模过程会进行简化和假设，影响模型的精度，利用相空间重构法将陀螺随机漂移时间序列扩展到高维相空间后，再进行超参数的求解，一方面可以充分体现序列信息，显著提高预测精度［10-12］;另一方面，可把一维标量序列转换为满足RVM要求的测试序列。

2.1 相空间重构

假设检测到的随机漂移序列是{xt}nt=1，根据坐标延迟重构法的Takens嵌入定理，状态空间中重构的一点状态向量可以表示为xt=(xt-(m-1)τ，xt-(m-2)τ，…xt)T，其中m为嵌入维数，τ为延迟时间。于是重构的预测模型为

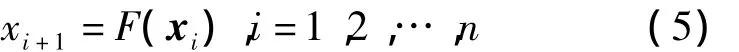
在这里可将xi+1看作RVM的目标值，而xi为输入值。

在相空间重构中，嵌入维数m和时间延迟τ的选取十分重要，其精度直接关系到相空间重构后描述奇异吸引子特征的不变量的准确度。大量实验表明m和τ的关系与重构相空间的时间窗tw密切相关(tw=(m-1)τ)，对于特定的时间序列，其tw相对固定，m和τ不恰当的配对将直接影响重构后的相空间结构与原空间的等价关系，因此相应地产生了m和τ的联合算法，如时间窗口法、C-C法等［13］。C-C法基于大量统计结果产生，计算量少，计算速度快，抗噪声性能好，本文采用C-C法来进行相空间重构参数的选择。

2.2 超参数求解

根据贝叶斯公式，由前面的模型推理得权值的后验概率分布为

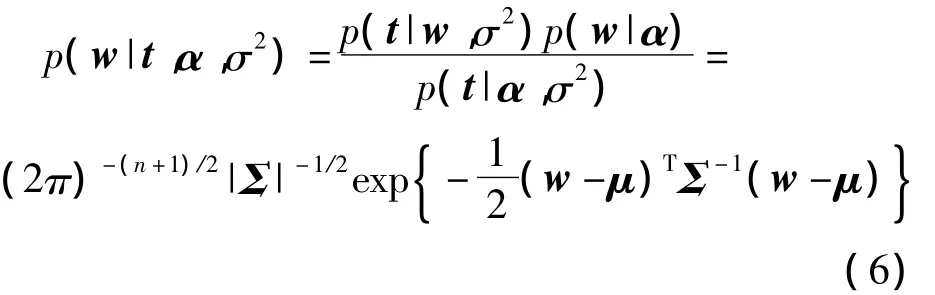
式中，σ2也作为RVMR的一个超参数，协方差矩阵Σ和均值向量μ分别为

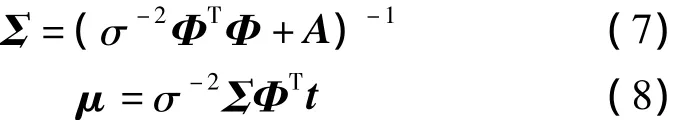
其中A=diag(α0，α1，…，αn)T为对角阵。RVM学习问题转化为求解超参数后验分布关于α和σ2的最大值问题。超参数α和σ2的优化，可通过EM算法近似求得

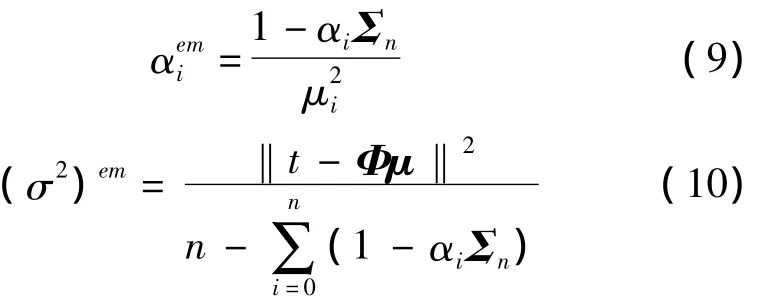
其中Σn是Σ中第i项在对角线上的元素。

先给出α和σ2初始值，然后通过式(9)、式(10)迭代计算，逐渐逼近优化的超参数α和σ2。在重新估计过程中，大部分的αi会趋向无穷大，其对应的wi为0，相关的核函数就会删除，其他权值不为零的训练样本成为关联向量(RV)，从而实现了稀疏化。RVM使用的核函数比SVM少得多，因此，在预测性能相当的情况下，RVM的稀疏性明显高于SVM。

2.3 回归预测

假设由2.2得到的超参数估计值为αM和σ2M，则对于新的测试样本，目标值t*后验概率分布可由式

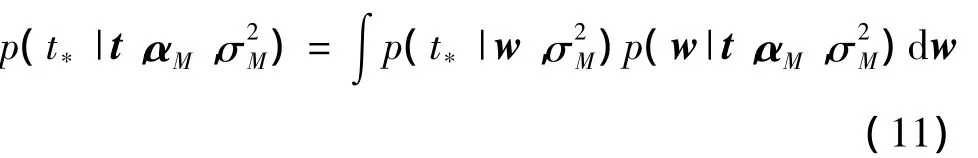
得到。式(11)中被积分的两项都服从高斯分布，故

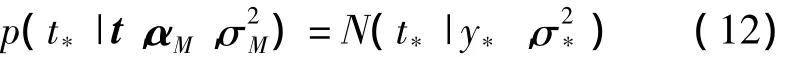
其中，期望y*及和方差σ2*分别为

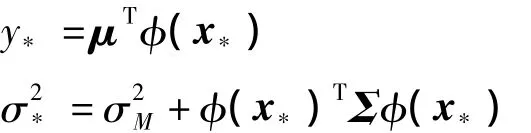
可以通过式(12)来预测t*的真实值，而σ2*为两预测变量的期望误差之和。

可见，RVM可以给出结果的后验概率，可根据训练数据自动调整其稀疏性，而SVM则需要由一个正规化参数来控制其稀疏性。

3 实验结果及分析

采集微惯性组合XW-ADU5600中x轴陀螺仪的静、动态输出数据，得到陀螺仪的输出序列，首先进行确定性误差补偿，得到陀螺仪随机漂移的时间序列。使用C-C法进行相空间重构时，数据超过3 000效果较好，因此本文选取其中长度为3 500的一段漂移序列进行实验，其中前2 500个数据作为训练数据，后1 000作为测试数据。通过C-C法获得嵌入维数m和时间延迟τ。

RVM权值是在贝叶斯框架下用最大似然方法来训练的，且RVM的核函数不受Mercer条件的限制，因此基函数可选用每个训练样本为中心的高斯函数。当缺少过程的先验知识时，在预测性能上径向基核函数要优于其他核函数。因此本文选用常用的径向基函数核K(xi，xj)=exp(-γ‖xi-xj‖2)，其中核函数的宽度参数γ取3.5，学习过程最大迭代次数选择1 200。

3.1 静态实验

图1为回归RVM在静态条件下的预测结果。原始1 000点漂移的RMSE标准差为0.105 3°/s，预测后的RMSE标准差为0.006 0°/s，陀螺仪精度提高了17.55倍。

为了证明RVM对陀螺漂移预测效果提高的有效性，将基于时间序列的ARMA(2，1)模型、RBF神经网络以及SVM用于陀螺静态漂移的预测，并对预测结果进行了比较，结果如表1所示。

表1 各种方法比较

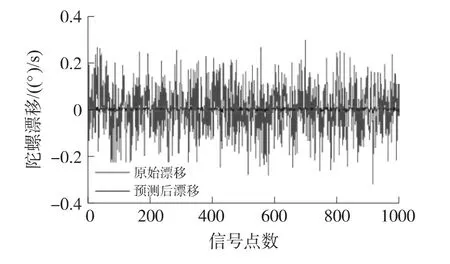
图1 静态条件下的预测结果

SVM和RVM相对ARMA、RBF神经网络具有较明显的优势，对于训练样本，SVM支持向量个数为126，而RVM相关向量个数为34，稀疏化效果明显优于前者，即RVM使用的核函数更少，结构更为简单，因此预测速度更快，占用内存更少。

3.2 恒速率实验

将陀螺仪放置在速率转台上控制转台分别以角速率20°/s、40°/s、60°/s旋转并且各采集1组数据。图2为回归相关向量机法在恒速率条件下的预测结果。

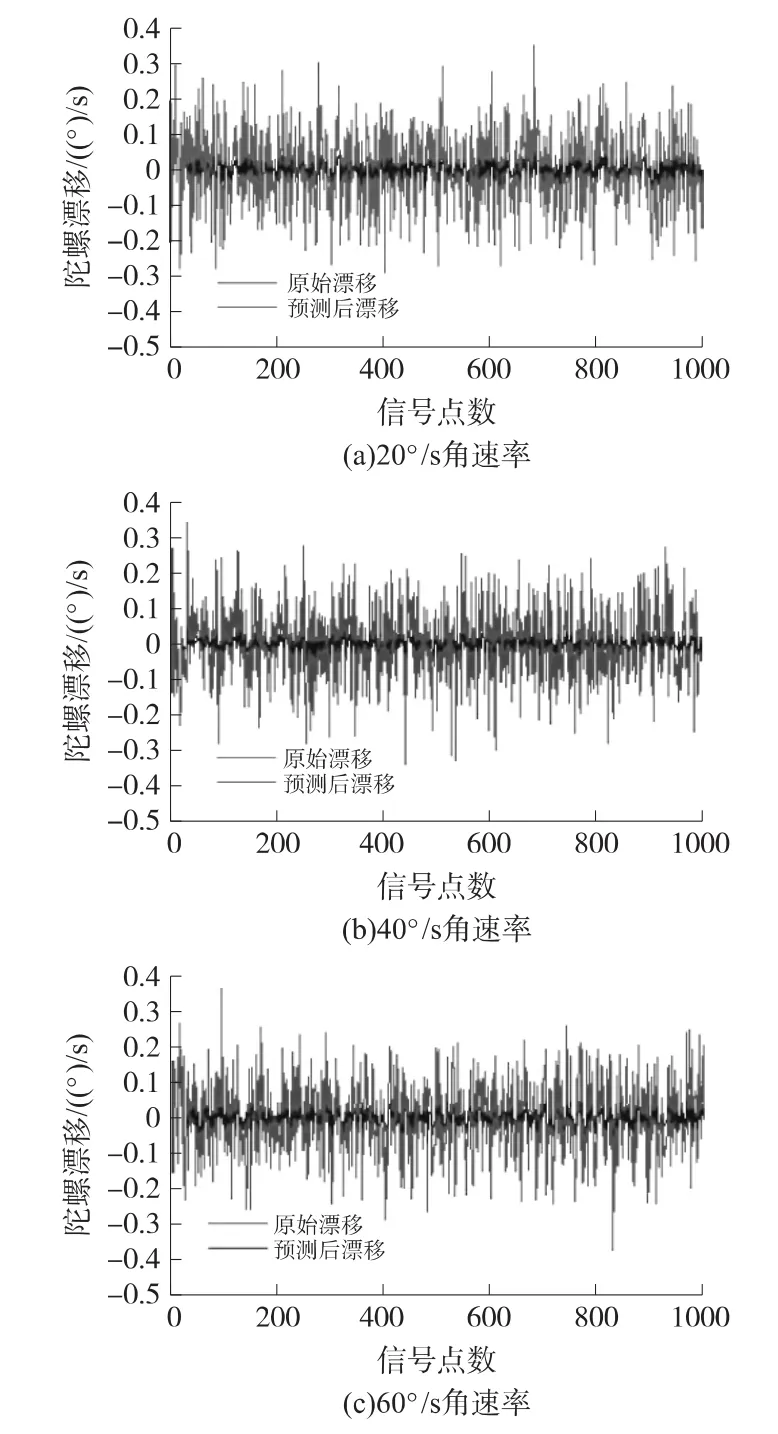
图2 恒速率条件下的预测结果

由图2可以直观的看出，预测后的漂移有明显的降低。具体原始数据和预测值的均值和RMSE标准差数值如表2所示。

表2 恒速率条件下预测结果

根据表内数据，在恒速率条件下RVM预测精度也有显著提高，证明RVM方法依然有效。

4 结束语

本文将基于贝叶斯的相关向量机法用于MEMS陀螺仪的随机漂移预测补偿，通过C-C法相空间重构将时间序列转换为相关向量机模型可用的数据形式，通过EM算法实现了相关向量机回归的超参数优化。实验结果表明，该方法克服了传统方法的不足，并弥补了支持向量机的缺陷，非常适合MEMS陀螺仪随机漂移的预测补偿，对于提高MEMS陀螺仪的应用精度具有一定的参考意义。

［1］陈旭光，杨平，陈意.MEMS陀螺仪零位误差分析与处理［J］.传感技术学报，2012，25(5):628-632.

［2］谈振藩，张勤拓.MEMS陀螺误差辨识与补偿［J］.传感器与微系统，2010，29(3):39-41

［3］牛春峰，刘世平，王中原.基于小波神经网络的MEMS陀螺输出预测方法［J］.海军工程大学学报，2012，24(2):29-32.

［4］宋吉磊，吴训忠，郭铃.微机电系统陀螺仪随机漂移误差建模与滤波研究［J］.导弹与航天运载技术，2012(4):35-38

［5］李泽民，段凤阳，马佳智.基于支持向量机的MEMS陀螺仪随机漂移补偿［J］.传感技术学报，2012，25(8):1084-1087

［6］Sebald D，Buckiew J.Support Vector Machine Techniques for Nonlinear Equalization［J］.IEEE Transactions on Signal Processing，2000，48(11):3217-3226.

［7］Wahyu C，Achmad W，Bo-Suk Y.Application of Relevance Vector Machine and Logistic Regression for Machine Degradation Assessment［J］.Mechanical System and Signal Processing，2010(24): 1161-1171.

［8］杨树仁，沈洪远.基于相关向量机的机器学习算法研究与应用［J］.计算机技术与自动化，2010，29(1):43-47

［9］Tipping M E.Sparse Bayesian Learning and the Relevance Vector Machine［J］.Journal of Machine Learning Research，2001，1(3): 211-244.

［10］吉训生，王寿荣.硅微陀螺漂移混沌特性分析及预测［J］.中北大学学报，2011，32(5):567-573.

［11］孙宏伟，房建成.基于多尺度多参量的硅MEMS陀螺仪漂移预测［J］.宇航学报，2009，30(2):591-594.

［12］李松，刘力军，谷晨.混沌时间序列预测模型的比较研究［J］.计算机工程与应用，2009，45(32):53-56.

［13］陆振波，蔡志明，姜可宇.基于改进的C-C方法的相空间重构参数选择［J］.系统仿真学报，2007，19(11):2527-2529.

沈强(1989-)，男，汉族，山东人，硕士研究生，仪器科学与技术专业，主要研究方向为MEMS陀螺仪误差补偿技术研究，shenq110@163.com;

刘洁瑜(1970-)，女，汉族，陕西西安人，博士学位，教授，硕士生导师，主要研究方向为惯性仪表及导航技术，主持并参与了多项重要科研项目，多次获得各级奖项，liujieyu128@163.com。

Random Drift Compensation of MEMS Gyros Based on Relevance Vector Machine

SHEN Qiang，LIU Jieyu*，WANG Qi，WANG Jiefei

(The Second Artillery Engineering University，Xi’an 710025，China)

A prediction and compensation method for MEMS gyroscope random drift based on relevance vector machine is proposed in this paper.Objected to the nonlinearity and indetermination of random drift error，the relevance vector machine modelis established，and the parameters ofprediction modelare gotby the Expectation Maximization (EM)algorithm.According to the chaotic property of random drift，the drift time-series which have been reconstructed by phase space reconstruction are used in this model.Both the train and test results indicate that this method can predict the gyroscope random drift accurately.Its prediction accuracy is superior to the time series method and support vector machine.Gyroscopes application precision can be further improved in practical system ifrandom drift is compensated by the predicting result.

MEMS gyroscope;random drift;relevance vector machine;phase space reconstruction;EM algorithm

V241.5

A

1004－1699(2014)05－0596－04

10.3969/j.issn.1004－1699.2014.05.005

2014-03-05

2014-04-22