基于系统最优维修策略的自动化车床管理的数学优化模型
2014-08-29黑龙江姚克俭
黑龙江 姚克俭
1 问题产生的背景
由于刀具损坏等原因会使工序出现故障,而工序出现故障是完全随机的,工作人员通过检查零件来确定工序是否出现故障,并且计划在刀具加工一定件数的零件后定期更换新刀具。
因此,给定检查间隔,对零件做检查,当发现零件不合格时则认为工序发生故障并立即进行停机检查,若实际存在故障则进行修理,无故障则继续生产;当检查发现零件合格则不干涉设备的工作,当到了定期更换刀具时刻,即使设备未出现故障,也进行刀具更新。
问题一:如果工序故障时产出的零件均为不合格品,正常产出的零件均为合格品,讨论该工序设计效益最好的检查间隔和刀具更换策略;
问题二:如果该工序正常时产出的零件不全是合格品,有2%为不合格品;而工序故障时产出的零件有40%为合格品,60%为不合格品,工序正常而误认有故障停机产生的损失费用为1500元/次,讨论该工序设计效益最好的检查间隔和刀具更换策略。
2 问题一的检查间隔与刀具更换策略模型
2.1 刀具故障记录的统计分析
通过检验可知:在α=0.10的显著水平下,刀具无故障工作时间近似服从N(μ,δ2)分布,由极大似然估计法得到μ=600,δ2=195.642.
假设Ho:X1的概率密度函数为f(x1)=,x∈R
将X(0~1200)分为12个区间,若Ho为真,则X1的概率密度为,查标准正态分布函数表可以得到概率Pi;所以
2.2 刀具无故障工作时间的概率分布
由于刀具损失故障占95%,整个无故障工作时间的分布近似于刀具无故障工作时间长的分布,即X~N(0.95μ,(0.95σ)2)。
2.3 刀具更换策略
在定期更换前,必须进行检查。若检查出故障,立即修理,若没有检查出故障,再进行定期更换。为了实际操作的方便,可以将定期更换周期定在第次检查后,即:若τ0为常数,则τ1=mτ0(m=1,2,…)。
2.4 问题一的数学模型
若X>τ1,损失为:L1=mt+k(t为检查费用,k为更换刀具的费用)
若 τ0<X<(n+1)τ0n=(0,1,2,…m-1);
损失为Ln=(n+1)t+d+((n+1)τ0-X)f(d为故障调节所需费用,f为产出不合格品的损失费用)
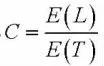
针对问题一的结果,我们采用蒙特卡罗法进行模拟检验,具体步骤如下:
⑴工序无故障工作时间X~N(600,9,1.642),用蒙特卡洛法模拟产生1000个无故障工作时间的伪随机数Xi(i=1,2,…1000)。
⑵给定检查间隔τ0和刀具定期更换间隔τ1,可以计算出Xi所对应的损失费用Li,
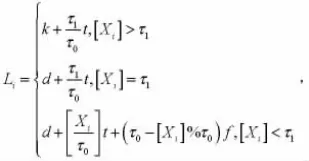
⑷对τ0,τ1进行搜索,求得单个零件损失费用C最小时的最优检查间隔τ0=18,定期更换刀具间隔τ1=378,相应的单个零件损失费用为4.16元。将问题一的结果与蒙特卡洛模拟的结果进行比较,列表如下:

由以上数据观察可发现用计算机模拟的结果与问题一的结果比较接近,因此说明问题一的结果比较稳定。
2.5 灵敏度分析
对于X~N(600,195.642)的正态分布,我们改变P(P为工序正常时不合格产品的比例)和(为工序故障时不合格产品的比例)得下表:
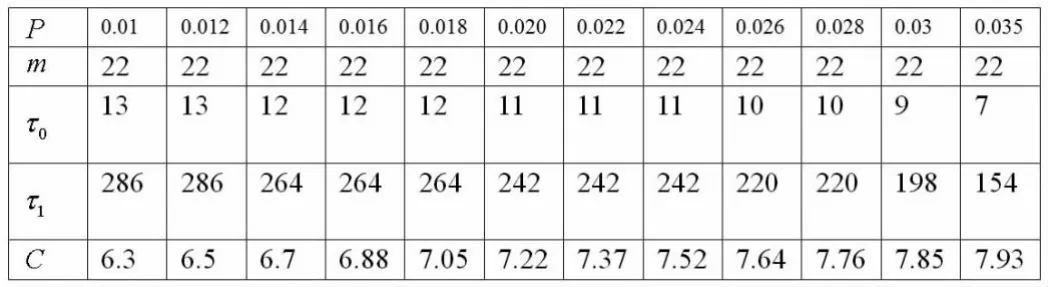
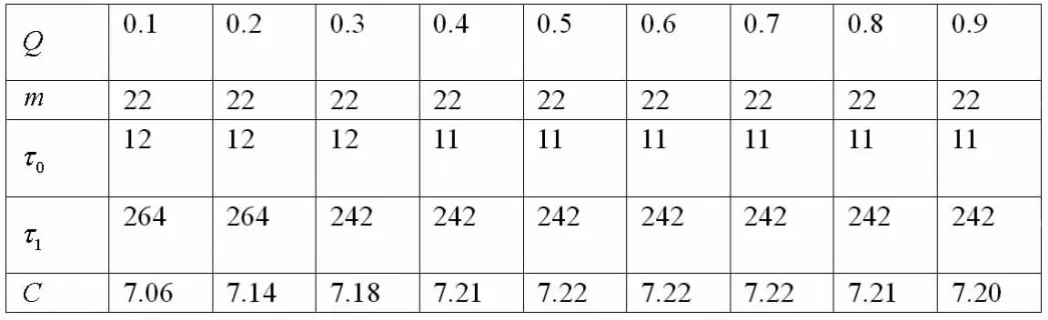
同理,改变误认为有故障而停机产生的损失费(1500元/次),发现它的变化对C的并不明显。
2.6 误差分析
我们在分析工序无故障的工作时间的同时,可以用刀具无故障工作时间的分布来近似判断,但是实际工序无故障的工作时间是未知的,若用正态分布来描述,其均值μ、均方差δ2的不确定性,对结果会造成一定的误差,我们用问题一的结果来进行误差分析,得下表:
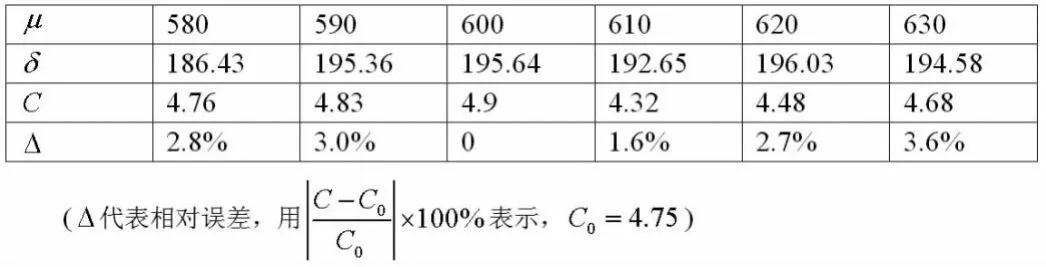
由此可知,均值μ、均方差δ的较小变化对结果的影响不大,因此我们采用的方法近似工序无故障分配工作时间是合理的。
3 问题二的检查间隔与刀具更换策略模型
3.1 问题二的分析
该问题需要考虑两种情况:⑴在工序正常工作时有可能检查到2%的不合格零件而误认为出现故障停机,发现误检后不进行换刀,继续正常工作,每次误停机将造成1500元的损失;⑵由于工序发生故障后仍有40%的合格零件产生,必然会导致因为检查到40%的合格零件而认为工序正常的错误,这样会增加不合格零件的数量和相应不必要的检查,从而使工序的损失增加。
3.2 问题二的数学模型
我们建立以单位合格零件的期望损失为目标的函数方程
系统工序合格零件的单位期望损失E(L)=
其中系统工序的总损失U总=U1(换刀前出现故障的损失)+U2(换刀前未出现故障的损失);假设整个系统共包括N次更新过程,换刀前出现故障的更新次数:N·F(T)(F(T)为以T更新周期的情况下工序出现故障的概率),换刀前未出现故障的更新次数:N·(1-F(T))。
所以 U1=N·(1-F(T))P1U2=N·F(T)P1P2
P1、P2为在两次总损失U1、U2下的单位更新过程的损失费用。
下面通过对一个换刀间隔T的研究来求P1、P2。
⑴换刀前未出现故障的更新过程的单位损失费用P1包括:一次换刀费用K;检查费用g1tg1=;误检测而停机造成的损失费用为×1500=30g1;在工序正常运行中产生的不合格零件的损失费用=单位换刀间隔T内产生的不合格零件数T×20%与单个不合格零件的损失f的乘积,即;
综合上述费用即为换刀前未出现故障的更新过程的单位损耗费用P1,
P1=K+g1T+30g1T+,
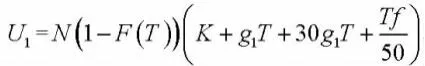
⑵同理,换刀前未出现故障的总损失U2=NF(T)P2,
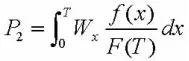
其中单位换刀间隔内的x点处发生故障的平均损失费用Wx包括:
①发生故障前的检查费用(g2-1)(g2表示包括故障后那次检查的故障前所有检查次数的和);
②发生故障前由于误检停机造成的损失费用 (g2-1)×2%×1500=30(g2-1);
④发生故障后的检查所需费用 ;
⑤对故障进行维修换刀的平均损失:(1-0.4g1-g2+1)d,其中0.4g1-g2+1为第g1-g2+1次检查时检查到合格品时的概率。
⑥发生故障后产生的不合格零件的平均损失费用:
当故障发生后第一次检查到合格零件而误认为是无故障发生直到检查出故障而进行换刀或维修为止的情况,这时损失可分为两个部分:
第一,发生故障产生后到第一次检查所产生不合格零件的损失,即为0.6hf。
第二,从发生故障后的第一次检查直到维修换刀时产生的不合格零件的平均损失费用为(H+0.4Tc+0.42Tc+…+0.4g1-g2T)c0.6f
整个系统的平均损失为
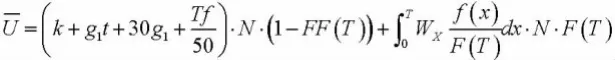
共产生的合格品零件总数为:
⑴换刀前未发生故障所产生的总的合格品零件个数:N[1-F(T)]T×98%;
⑵换刀前发生故障所产生的总的合格品零件个数:
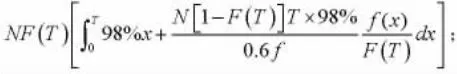
考虑到一般设备使用期限内可分为稳定期和不稳定期。这里的稳定是指故障少,而所谓不稳定是指故障比较多。
可以改进等间隔检查方式,使其在稳定期内检查间隔长,在不稳定期内检查间隔短,从而获得更高的效益。也就是说故障率大时(即设备运行到时刻未发生故障的条件下,[x,x+dx]时间内设备发生故障的条件概率最大),则单位时间内的检查次数n(x)也随之增大,令n(x)=,其中
p(x)dx是设备在[x,x+dx]内发生故障的概率,1-F(x)是时刻设备未发生故障的概率。
相对于问题一,由于问题二发生故障后仍有40%的合格品产生,因此给检查带来了困难,为了尽量减少误检造成的损失,于是相应的检查间隔变大而换刀时间间隔减小,从而单位期望值也由4.75变为9.047。
设计安装工序自动检测调节装置,对于每个零件进行检查,假设检查费用为零,下面给出的自动检测调节系统可以有效避免上述问题中正常工序而误认为故障停机产生的损失,从而降低单位零件的平均管理成本。
设为自动检测调节装置统计的件数,本系统按顺序检查个零件出现的不合格品数,建立动态检测模式,自动记录按顺序检查的和个零件中出现的不合格品数,并且自动记录工序正常时所检测的零件个数,有以下四种情况:
⑴顺序统计的个零件,次品率低于2%,认为工序正常,继续生产;
⑵顺序统计的个零件,次品率高于2%低于60%,但所有已检查零件的次品率低于2%,认为工序正常,继续生产;
⑶顺序统计的个零件,次品率高于60%,但所有已检查零件的次品率低于2%,认为工序正常,继续生产;
⑷顺序统计的个零件,次品率高于60%,并且所有检查零件的次品率高于2%,认为工序故障,系统自动发出信号并进行调节。
若考虑到其它故障,我们将上述模型的假设条件改为:其它故障与刀具故障的发生相互独立,其它故障服从于区间[0,22800]的均匀分布,该模型的表达式依然成立,只需遍历其它故障的发生、刀具故障的发生以及第一次检测出不合格品这三个事件的所有情况即可推出,只不过其形式相当复杂,有待于我们进一步完善。
4 模型的评价与改进
该模型通过对检查间隔和换刀间隔进行遍历搜索,得到了固定检查间隔下的最优解。它是以单位期望效益为目标的更新报酬定理的改进与推广,广泛适合于自动化2的管理系统,对多道工序和多种零件的复杂车床管理系统有一定的指导意义。
[1]蔡俊.可靠工程学[M].哈尔滨:黑龙江科学技术出版社,1990,2.
[2]沈玉波,冯敬海.可修系统的最优化检测更新模型[J].数学实践与认识,1999,03.
