橡胶纳米复合材料计算机模拟研究进展与挑战

刘 军， 沈建祥， 张立群

(北京化工大学，北京 100029)

1 前 言

轮胎用橡胶复合材料通常会加入炭黑或白炭黑等粉体，其原生粒子(Primary Particle)尺寸在100 nm以下，可被定义为橡胶纳米复合材料。随着各种新型纳米材料被发现与成功实现大规模的可控合成，如碳纳米管与石墨烯，这进一步丰富了橡胶纳米复合材料的种类。目前一致认为，橡胶纳米复合是实现其高效增强的必要手段[1]。本文针对橡胶常用纳米增强颗粒——三维球状(炭黑或白炭黑)、二维片状(粘土或石墨烯)与一维杆状(碳纳米管)，橡胶纳米复合材料关键结构与性能——分散及机理、界面结合(应力传递)、静态力学(应力应变)与动态力学(滞后损失)，总结了作者课题组在过去几年里，借用计算机模拟技术(分子动力学模拟)对这些关键基础科学问题的研究成果。对分子动力学模拟，采用典型的珠簧模型(Bead-Spring Model)来模拟橡胶分子链，粗粒度模型来模拟不同形状的纳米颗粒[2]。模拟的力场包括Lennard-Jones相互作用能与有限伸长非线性弹性势能(Finite Extensible Non-Linear Elastic)分别模拟非键和能(Non-Bonded Interaction)与键和能(Bonded Interaction)[3-4]。

2 橡胶纳米复合材料结构性能关系模拟

2.1 分散及机理

成功制备橡胶纳米复合材料的首要关键问题是如何实现颗粒纳米尺度的分散。模拟了球状纳米颗粒[5]与表面接枝化学改性纳米颗粒[6]在橡胶分子链中的分散行为，系统研究了分子链与颗粒界面相互作用、颗粒填充分数、接枝分子链长与接枝密度、本体分子链长与本体分子链与接枝分子链相容性对分散的影响。由图1a所示，发现对于平衡态体系而言，在界面相互作用为εnp=2.0时，Snapshot图显示获得了一个最佳分散。从图1b可以看出，通过计算周围临近纳米颗粒的平均数目与第二维里系数，进一步定量地验证了该结果。该模拟结论与Schweizer等人理论预测的结论一致。通过计算颗粒-颗粒总的相互作用能与周围临近纳米颗粒的数目，模拟结果表明：存在一个最佳的接枝密度以获得纳米颗粒的均匀分散(如图2a，b所示)。同时，也考察了橡胶分子链长与片层相互作用能、温度、分子链长、表面改性剂与层间距对插层动力学的影响[7]。采用第二勒让德多项式表征了分子链在层间的取向排列，结果表明，靠近上下板处分子链平行于板排列，在远离板处分子链垂直于板排列，并且该趋势随着分子链与板间作用能增大而更明显(如图3所示)。对杆状颗粒，也发现存在一个最佳的界面作用来获得均匀分散的颗粒。通过对杆表面化学接枝或施加剪切场，均能有效降低其聚集程度[8]。

2.2 界面结合

图1 不同界面相互作用下纳米颗粒分散的Snapshot图(a)和周围临近纳米颗粒的平均数目与第二维里系数随界面相互作用的变化(b)Fig.1 Snapshots of the dispersion state of spherical with respect to the interfacial interaction(a) and the change of the number of neighbor fillers and second virial coefficient as a function of the polymer-filler interaction strength(b)

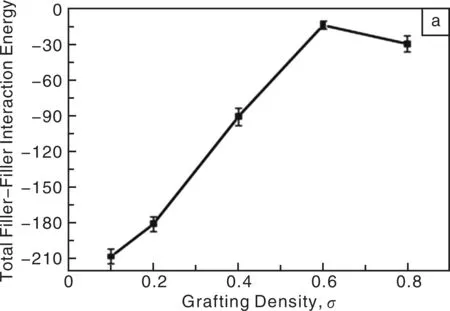
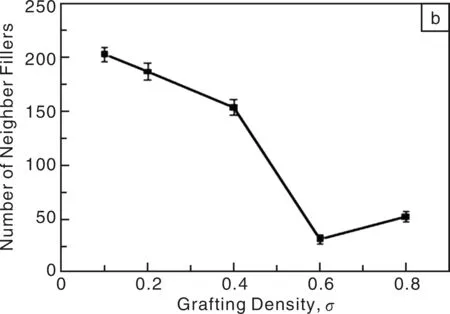
图2 颗粒-颗粒总的相互作用能(a)和周围临近纳米颗粒的数目(b)随接枝密度的变化Fig.2 The change of the total filler-filler interaction energy(a)and the number of neighbor fillers(b) as a function of the grafting density

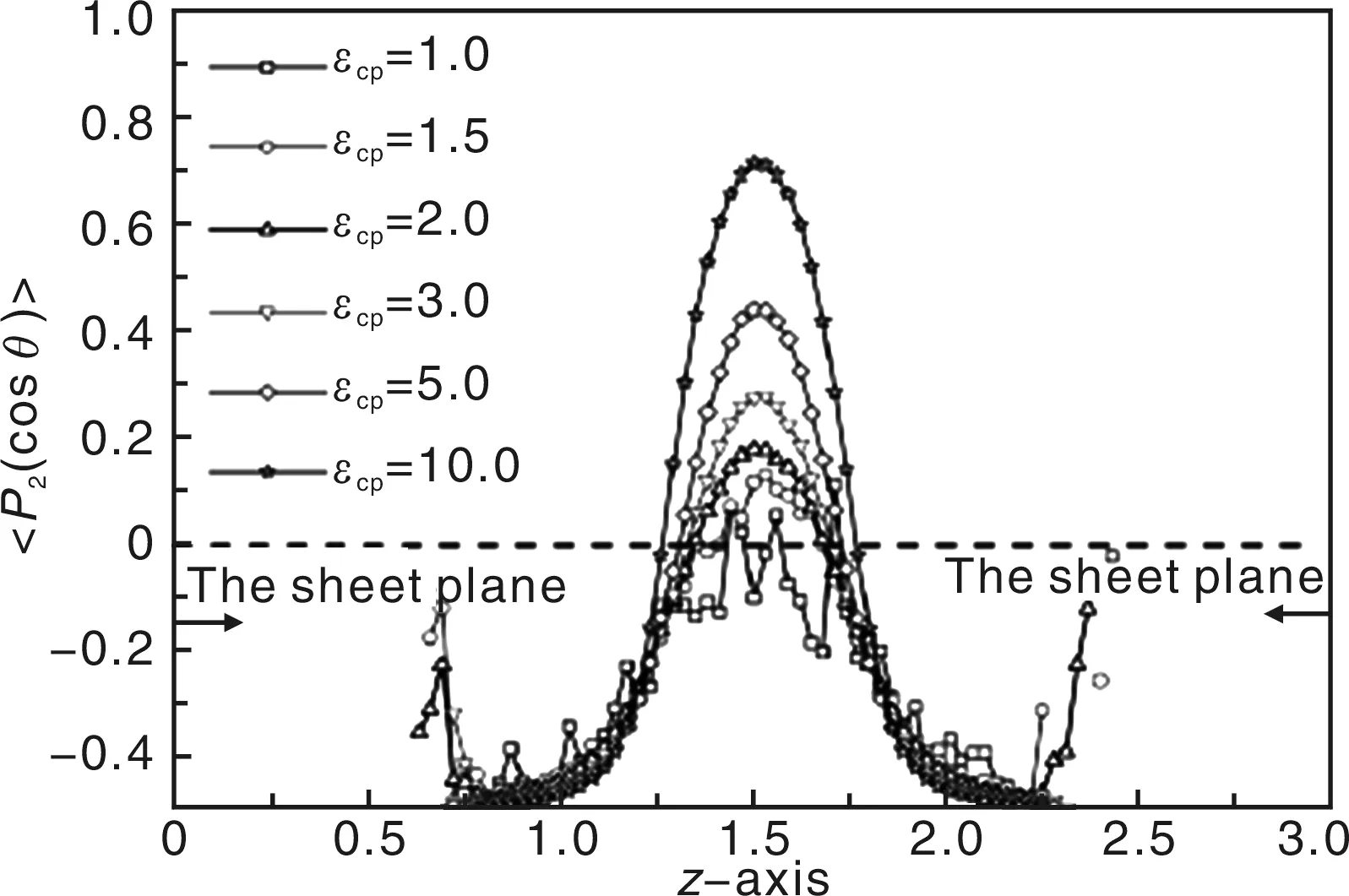
图3 片层间不同界面作用下分子链键取向离板间距的变化Fig.3 Bond orientation as a function of its distance from clay sheet surface in the case of different interfacial interactions

复合材料能否有效将力从橡胶基体传递给纳米颗粒取决于界面结合的好坏。考察了分子链与球状纳米颗粒界面结合状态[9]。结果表明：界面区尺寸大概为分子链均方根回转半径Rg，与界面相互作用和颗粒尺寸无关。在弱界面作用下，分子链垂直于颗粒表面吸附，而在强界面作用下，分子链包覆在颗粒表面吸附(图4a)，同时界面区由不同分子链的链段构成(图4b)。界面区分子链的取向与活动性由界面焓(Interfacial Enthalpy)控制，而其尺寸与构象由构象熵(Conformational Entropy)控制。在强界面(类似氢键)作用下，模拟发现界面区分子链依然具有一定的活动性，并能发生吸附-解吸附过程(图4c)，该发现与实验上报道的界面区存在聚合物玻璃化层结果相反[10]。

同时，也探讨了橡胶分子链与片状纳米颗粒间界面相互作用(图5)[11]，发现界面区存在聚合物活动性梯度。由于片上存在很多作用点，在类似氢键作用情况下，会出现聚合物玻璃化层，并对不同作用强度下界面区分子链吸附-脱吸附动力学过程进行了表征。

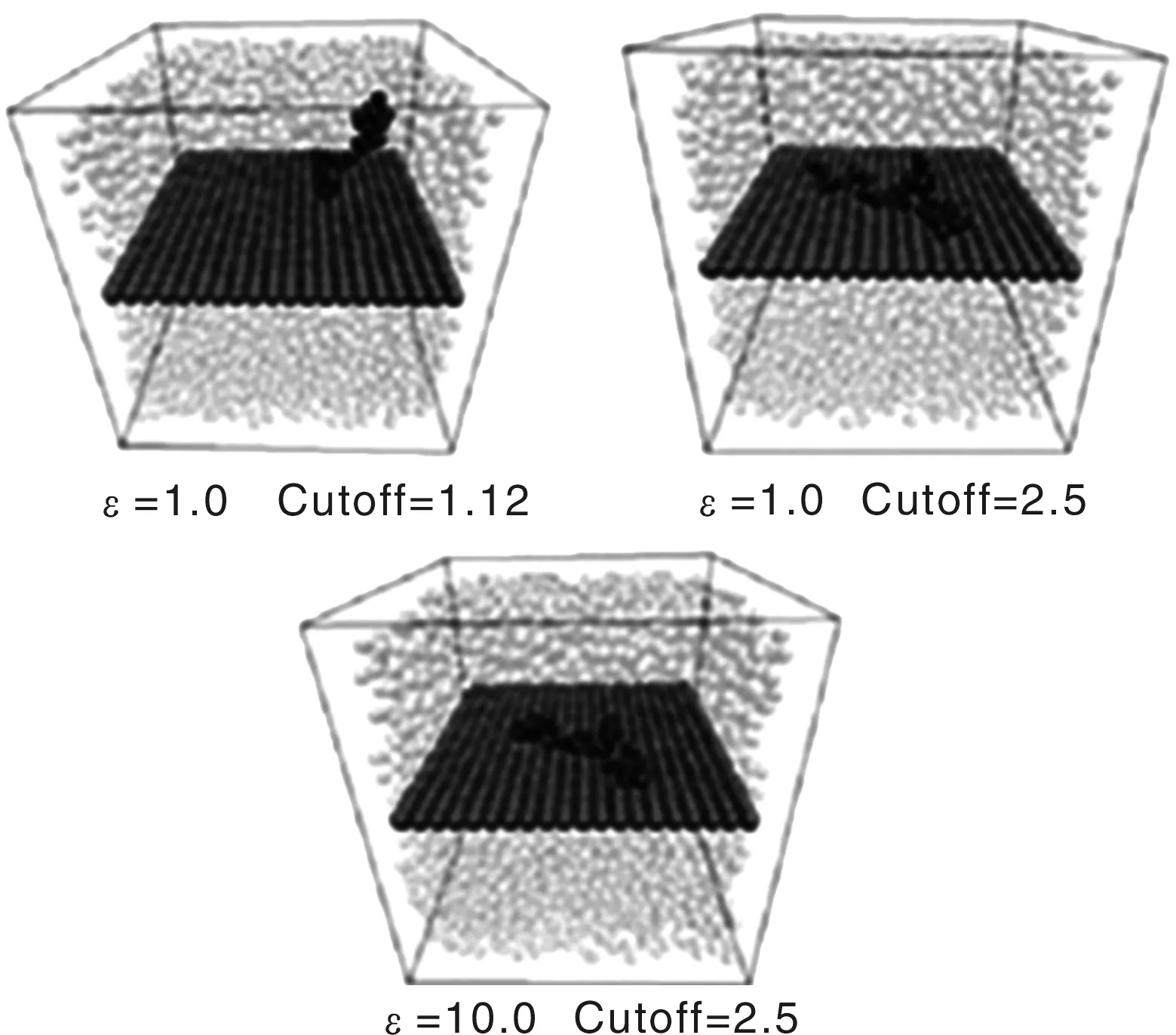
图5 不同界面作用下分子链在片状颗粒表面的吸附状态Fig.5 Adsorption state of displayed single chain on sheet surface

2.3 静态力学性能

纳米颗粒的加入能明显提高橡胶基体的力学性能，但对其力学增强机理依然不清楚。模拟单轴拉伸(图6a)[9]，发现在一定界面作用下，存在一个最佳增强分数(图6b与6c)，原因是分子链取向存在一个最佳填充分数。模拟发现球状纳米颗粒增强橡胶来自于两方面：一是颗粒诱导分子链取向与排列，二是分子链吸附临近颗粒形成桥链在大变形下的有限链伸长。前者受颗粒含量、颗粒尺寸与颗粒-分子链相互作用的影响，后者随界面物理化学作用的增加而变得更明显。同时，分析出纳米颗粒增强塑料基体效果比较差的原因在于纳米颗粒的引入反倒降低了拉伸过程中分子链的取向度(图6c)。提出了一个临界粒子间距(Critical Particle-Particle Distance, CPPD)来解释复合材料拉伸强度随填充分数呈现的逾渗现象，并且解释了高效增强必须加入高填充的纳米颗粒的原因[12]。

2.4 动态力学性能

如何有效降低轮胎用橡胶纳米复合材料的滞后损失是制备绿色轮胎首要解决的关键科学问题。首次模拟了碳纳米弹簧的引入对橡胶基体粘弹性的影响(图7a所示)[13]。有文献报道，碳纳米弹簧具有力学可回复变形[14]，与橡胶复合后，可用图7b中的粘弹性模型来描述，即两个弹簧与一个粘壶的并联。通过对其拉伸-回复过程的模拟(图7c)，发现体系动态滞后损失(Dynamic Hysteresis Loss, DHL)随着碳纳米弹簧弹性系数的增加而逐渐减小(图7d), 分析其中的原因是随着碳纳米弹簧弹性系数的增大，在拉伸过程中储存的能量更多，在回复过程中会更有效带动周围橡胶分子链的运动，降低体系内摩擦与滞后损失。该发现为工业上制备低滞后损失的轮胎提供了科学依据与理论指导，也为碳纳米材料的大规模工业化应用提供了新的途径。该研究结果在2013APS March meeting上以题为 “Material Science Advances Energy Efficiency”进行了Highlight[15]。

图6 球状填充体系单轴拉伸示意图(a),低填充分数(b)与高填充分数(c)下应力应变曲线，玻璃态下不同填充分数下分子链键取向随拉伸应变变化示意图(d)Fig.6 Uni-axial tension of spherical NPs filled rubber system(a), stress-strain curves at low filler volume fraction(b) and high filler volume fraction(c), and bond orientation of glassy polymers with different filler volume fraction(d)

对橡胶纳米复合材料，实验上发现体系储能模量随应变幅度的增大会逐渐变小，且该非线性行为随着填充分数的逐渐增大而变得更明显，该现象也被称为 “Payne效应”。Payne效应的出现会增大体系的滞后损失。但目前对其产生的分子机理还不清楚。模拟了两种不同分散状态下(如图8a与9a)其模量随应变的变化,其中图8a为纳米颗粒直接接触聚集，图9a为纳米颗粒通过吸附分子链而连接成网。对这两种不同初始分散体系，均发现随着填充分数的增加，其非线性行为逐渐变得明显，如图8b与图9b。前一种分散态其Payne效应由颗粒直接接触聚集引起，而后一种分散态则是由分子链同时吸附多个颗粒成网而导致的。通过逐渐增大颗粒-颗粒相互作用能(图8c), 颗粒-分子链相互作用能(图9c)，其非线性行为均会变得更加明显。

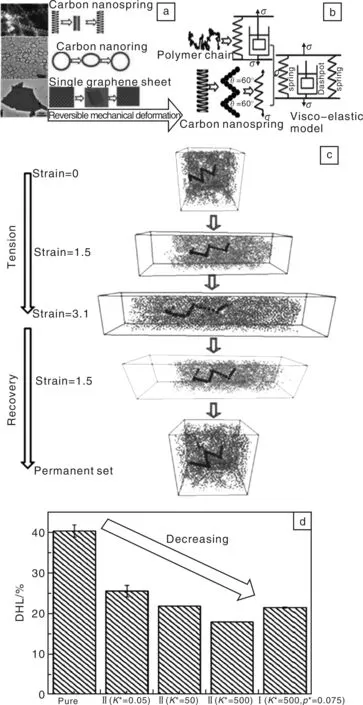
图7 碳纳米弹簧、碳纳米环与单片石墨烯力学可回复变形示意图(a)，碳纳米弹簧填充橡胶体系粘弹性模型示意图(b)，碳纳米弹簧填充橡胶体系拉伸回复过程示意图(c)，动态滞后损失随着碳纳米弹簧弹性体系数逐渐增大而减小(d)Fig.7 Schematics of the reversible mechanical deformation of carbon nanospring, carbon nanoring and single graphene sheet(a), the visco-elastic model of carbon nanosprings filled rubber system(b), snapshot of the reversible mechanical deformation of carbon springs filled rubber system(c), and the variation of the dynamic hysteresis loss(DHL) as a function of the elastic constant of the carbon nanosprings(d)

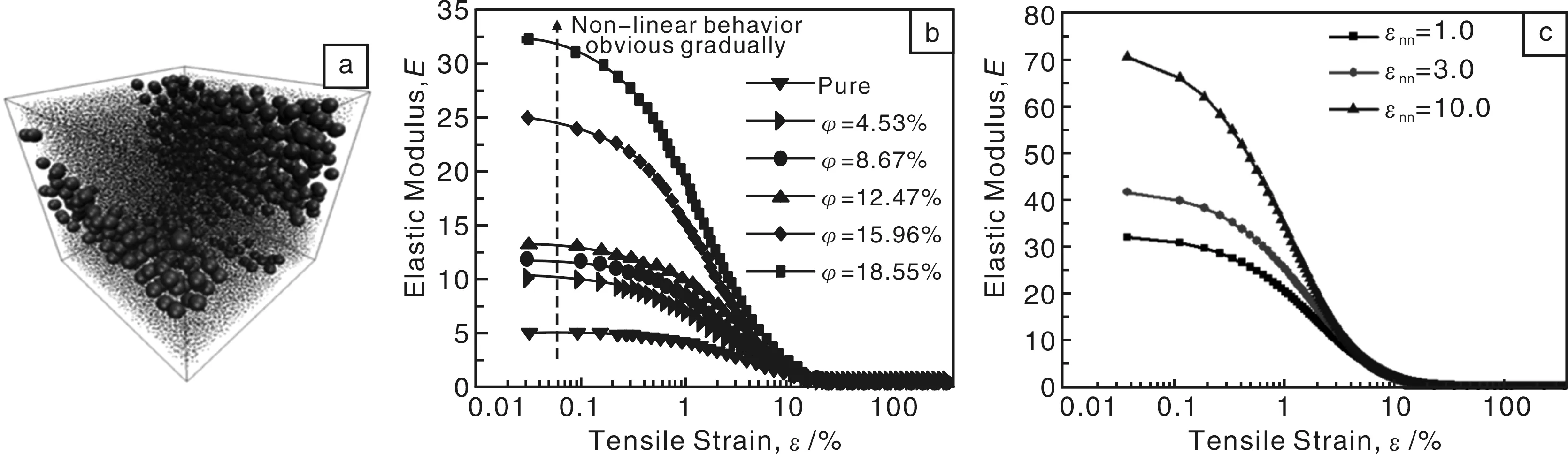
图8 初始状态为球状颗粒聚集的体系(a), 非线性行为随着填充分数(b)与颗粒-颗粒相互作用能(c)增加而逐渐增大Fig.8 Aggregation state of spherical NPs as the initial state(a), the non-linear behavior becoming more obvious with the increase of the filler volume fraction(b) and the NP-NP interaction strengthening(c)

图9 初始状态为球状颗粒分散的体系(a), 非线性行为随着填充分数(b)和颗粒-聚合物相互作用能(c)增加而逐渐增大Fig.9 Dispersion state of spherical NPs as the initial state(a), the non-linear behavior becoming more obvious with the increase of the filler volume fraction(b) and the NP-polymer interaction strengthening(c)

3 结 语

橡胶纳米复合材料多层次多尺度主要表现在：对分子链从重复单元(≈1 nm)→链段(≈5～10 nm)→分子链回转半径与分子链末段距(≈50～100 nm), 对球状填充颗粒从原生粒子(≈20～50 nm)→聚结体(≈100～200 nm)→聚集体(≈104～106nm)，对各向异性颗粒其长径比会达到1 000左右(长度会达到mm级)而容易团聚。要通过计算机模拟科学全面地建立橡胶纳米复合材料微观结构与性能关系，还有如下难题需要解决。

(1)从分散与界面研究入手，建立复合材料双网络结构模型(化学交联网络与大分子链-颗粒形成的物理网络)。

(2)系统模拟在动态应变与静态拉伸、压缩与剪切下网络结构的演化行为及规律。

(3)构建网络结构参数与动态粘弹性(储能模量、损耗模量与损耗因子)、动态裂纹引发与扩展、应力应变(本构关系)的定量模型。

参考文献 References

[1] Hamed G H, Reinforcement of Rubber[J].RubberChemistryandTechnology, 2000, 73:524.

[2] Zeng Q H, Yu A B, Lu G Q. Multiscale Modeling and Simulation of Polymer Nanocomposites[J].ProgressinPolymerScience, 2008, 33 (2): 191-269.

[3] Liu J, Cao D P, Zhang L Q,etal. Molecular Dynamics Simulation for Insight into Microscopic Mechanism of Polymer Reinforcement[J].PhysicalChemistryChemicalPhysics, 2009, 11:11 365.

[4] Liu J, Zhang L Q, Cao D P,etal. Computational Simulation of Elastomer Nanocomposites: Current Progress and Future Challenges[J].RubberChemistryandTechnology, 2012, 85: 450.

[5] Liu J, Gao Y Y, Zhang L Q,etal. Nanoparticle Dispersion and Aggregation in Polymer Nanocomposites: Insights from Molecular Dynamics Simulation[J].Langmuir, 2011, 27: 7 926.

[6] Shen J X, Liu J, Gao Y Y,etal. Revisiting the Dispersion Mechanism of Grafted Nanoparticles in Polymer Matrix: A Detailed Molecular Dynamics Simulation[J].Langmuir, 2011, 27: 15 213.

[7] Gao Y Y, Liu J, Shen J X,etal. Microstructure and Intercalation Dynamics of Polymer Chains in Layered Sheets[J].RSCAdvances, 2013(3): 21 655.

[8] Gao Y Y, Liu J, Shen J X,etal. Molecular Dynamics Simulation of Dispersion and Aggregation Kinetics of Nanorods in Polymer Nanocomposites[J].Polymer, 2014, 55:1 273.

[9] Liu J, Wu S Z, Zhang L Q,etal. Polymer-Nanoparticle Interfacial Behavior Revisited: A Molecular Dynamics Study[J].PhysicalChemistryChemicalPhysics, 2011, 13:518.

[10] Merabia S, Sotta P, Long D R. A Microscopic Model for the Reinforcement and the Nonlinear Behavior of Filled Elastomers and Thermoplastic Elastomers (Payne and Mullins Effects)[J].Macromolecules, 2008, 41:8 252.

[11] Gao Y Y, Liu J, Zhang L Q,etal. Existence of a Glassy Layer in the Polymer-Nanosheet Interface: Evidence from Molecular Dynamics[J].MacromolecularTheoryandSimulation, 2013, 23, 36.

[12] Wang Z H, Liu J, Wu S Z,etal. Novel Percolation Phenomena and Mechanism of Strengthening Elastomers by Nanofillers[J].PhysicalChemistryChemicalPhysics, 2010, 12:(12), 3 014-3 030.

[13] Liu J, Lu Y L, Tian M,etal. The Interesting Influence of Nanosprings on the Viscoelasticity of Elastomeric Polymer Materials: Simulation and Experiment[J].AdvancedFunctionalMaterials, 2013, 23:1 156.

[14] Poggi M A, Boyles J S, Bottomley L A. Measuring the Compression of a Carbon Nanospring[J].NanoLett, 2004, 4(6): 1 009-1 016.

[15] Liu Jun(刘 军), Zhang Liqun(张立群), Cao Dapeng(曹达鹏).TheInterestingInfluenceofNanospringsontheViscoelasticityofElastomericPolymerMaterials:SimulationandExperiment(纳米弹簧调节聚合物粘弹性的模拟与实验研究)[EB/OL].(2013-03-18)[2014-04-04].http://www.newswise.com/articles/2013-aps-march-meeting-to-feature-advances-in-energy-armor-quantum-communication-medicine-and-much-more.