不确定参数分数阶Lorenz混沌系统的混合函数投影同步
2014-08-28刘景琳
刘景琳
(广东技术师范学院电子与信息学院,广州 510665)
自1990年Pecora和Carrol[1]对2个不同初始条件的相同混沌系统实现同步以来,混沌同步在各个科学领域的潜在应用取得了许多研究成果.至今相继提出了各种同步方案[2-3]:完全同步、相同步、反相同步、广义同步、滞后同步等.1999年,Mainieri和Rehacek[4]在部分线性系统中观察到一种新的同步现象——投影同步,即驱动系统和响应系统之间的对应变量按照一定的比例因子演化,它是一类特殊的广义同步现象.目前对于投影同步的研究大多是基于驱动系统和响应系统之间按某常数(投影同步)或不同的常数(修正投影同步)比例因子进行同步,或按某一函数(函数投影同步)或不同函数(修正函数投影同步)的比例因子进行同步[5].近几年,有学者将修正函数投影同步中对称的比例函数矩阵变换为更一般的混合函数矩阵,实现了更具一般意义上的函数投影同步[6].同时在很多实际情况下,限于测量条件和工具的限制,很难知道系统参数的真值,系统的全部参数是不确定的或部分不确定的,因此在研究系统同步时兼具研究系统参数的辨识更具实际意义.
然而,先前的许多研究成果往往是在整数阶混沌系统领域,研究分数阶混沌系统很少.但在现实中,分数阶系统却更具有普遍性,具有比整数阶系统更为复杂丰富的动力学特性,具有更大的密钥空间,因而对分数阶混沌系统的同步研究具有更重要的理论价值和现实意义.
基于分数阶系统稳定性理论,本文通过设计自适应控制器和参数更新律,提出了一种自适应混合函数投影同步方案,用分数阶Lorenz混沌系统进行仿真实验,并实现对响应系统所有不确定系统参数的辨识.
1 分数阶微分和系统模型描述
分数阶微分的定义有几种,本文采用常用的Caputo定义[7],其数学表达式如下:

(1)
其中Dq表示分数阶微分的Caputo定义,Γ(·)为伽马函数,l-1<α 考虑下述形式的驱动—响应系统 Dqdx=f(x), (2) Dqry=g(y,θ)+Ω, (3) e=y-K(x)x, (4) eθ=θ-θ0, (5) Dqrθ=p(x,y,θ), (6) 其中K(x)是n×n实矩阵,矩阵元素kij(x)(i,j=1,2,…,n)是连续有界函数,θ0为θ的真值,p(x,y,θ)是m×(n+m)的实矩阵,m是不确定系统参数的数目. 当K(x)是实对称函数矩阵时,混合函数投影同步退化为修正函数投影同步或函数投影同步;当K(x)是实常数对称矩阵时,混合函数投影同步变成修正投影同步或投影同步;当K(x)是单位矩阵时,同步为完全同步;当K(x)是负单位矩阵时,同步为反同步.由此可见,以往相关文献所研究的各种投影同步都是混合函数投影同步的特例. 对于响应系统(3),定义一个补偿控制器Ω1(x)=Dqr(K(x)x)-g(K(x)x,θ0),则响应系统(3)中的控制器Ω可表示为Ω=Ω1(x)+Ω2,Ω2为一个n×1的向量函数阵.因此,响应系统(3)可化为Dqry=g(y,θ)+Dqr(K(x)x)-g(K(x)x,θ0)+Ω2.对式(4)两边求分数阶导数: Dqre=Dqry-Dqr(K(x)x)= g(y,θ)-g(K(x)x,θ0)+Ω2, (7) (8) 由于常数的Caputo微分为零,结合参数更新律式(6),得 Dqrθ=Dqr(θ-θ0)=p(x,y,θ)= (9) 联立式(8)和式(9),得 (10) 定理1 假设B(x,y,θ0)和满足下式 (11) 则 (12) 其中P是实对称正定矩阵,Q是实对称半正定矩阵,H表示矩阵的共轭转置. 证明假设为的任一特征值,其对应的特征向量为ξ,则 (13) 上式两边左乘ξHP,得 (14) 同理,可得 (15) 式(14)、(15)相加,得 结合式(11),上式可化为 (16) 又因为P是实对称正定矩阵,Q是实对称半正定矩阵,所以|arg|≥π/2>qrπ/2. 由分数阶系统稳定性理论[8]知式(12)成立,即驱动系统(2)和响应系统(3)达到自适应混合函数投影同步.证毕. 分数阶Lorenz混沌系统的微分方程为[9] (17) 图1 分数阶Lorenz系统的混沌吸引子 由式(2)、(3)和式(17)列写分数阶Lorenz驱动系统和响应系统如下: (18) (19) 其中,系统参数真值(a0,b0,c0)=(10,28,8/3). 响应系统的不确定系统参数θ=(a,b,c),参数更新律为 Dqrθ=p(x,y,θ)= (20) 依据上节的内容,可以得出 A(x,y,θ0)= 图2 Lorenz混沌系统的同步误差曲线 图3 不确定系统参数的辨识曲线 本文基于分数阶系统稳定性理论,针对分数阶Lorenz混沌系统,提出了一种自适应混合函数投影同步方法,并实现了对响应系统所有不确定系统参数的辨识.仿真实验表明,响应系统在受控的短时间内能与驱动系统达到同步.相对于修正函数投影同步和函数投影同步采用的对称函数矩阵,本文采用的混合函数矩阵的每个元素都不为零,同步是在响应系统和驱动系统之间按照任意给定的比例函数加权求和进行同步,因此增加了同步后混沌系统吸引子的结构复杂程度和混沌程度,所以利用混合函数投影同步进行保密通信可增加加密信息的安全性.对通信双方以外的第三方而言,混合函数是不可预知的,从而增加了加密信号在传输过程中被截获破译的难度,获得更好的安全性.混合函数投影同步在外界干扰下和在复杂网络中的同步及控制问题将是我们下一步研究的方向. 参考文献: [1] Pecora L M, Carroll T L. Synchronization in chaotic systems[J]. Physical Review Letters, 1990, 64(8): 821-824. [2] Zhang Q J, Lu J A. Chaos synchronization of a new chaotic system via nonlinear control[J]. Chaos, Solitons and Fractals, 2008, 37(1): 175-179. [3] 李丰国,林木欣. 混沌同步的电路演示系统[J]. 华南师范大学学报:自然科学版,1998(3): 58-64. Li F G, Lin M X. A circuit demonstrating system of chaotic synchronization[J].Journal of South China Normal University:Natural Science Edition, 1998(3): 58-64. [4] Mainieri R, Rehacek J. Projective synchronization in three-dimensional chaotic systems[J]. Physical Review Letters, 1999, 82(15): 3042-3045. [5] Du H Y, Zeng Q S, Wang C H. Modified function projective synchronization of chaotic system[J]. Chaos, Solitons and Fractals, 2009, 42(4): 2399-2404. [6] Zhou P, Yang X Y. A novel hybrid function projective synchronization between different fractional-order chaotic systems[J]. Discrete Dynamics in Nature and Society, 2011: Art 496846, 15pp. [7] Podlubny I. Fractional differential equations[M]. San Diego: Academic Press,1999. [8] Ogata K.Modern control engineering[M]. 3rd ed. Upper Saddle River: Prentice Hall, 1998. [9] Grigorenko I, Grigorenko E. Chaotic dynamics of the fractional Lorenz system[J]. Physical Review Letters, 2003, 91(3): 034101. [10] Zhou T S, Li C P. Synchronization in fractional order differential systems[J]. Physica D: Nonlinear Phenomena, 2005, 212(1/2): 111-125.
2 自适应混合函数投影同步方案






3 数值仿真
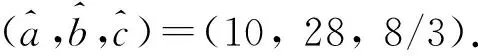


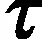

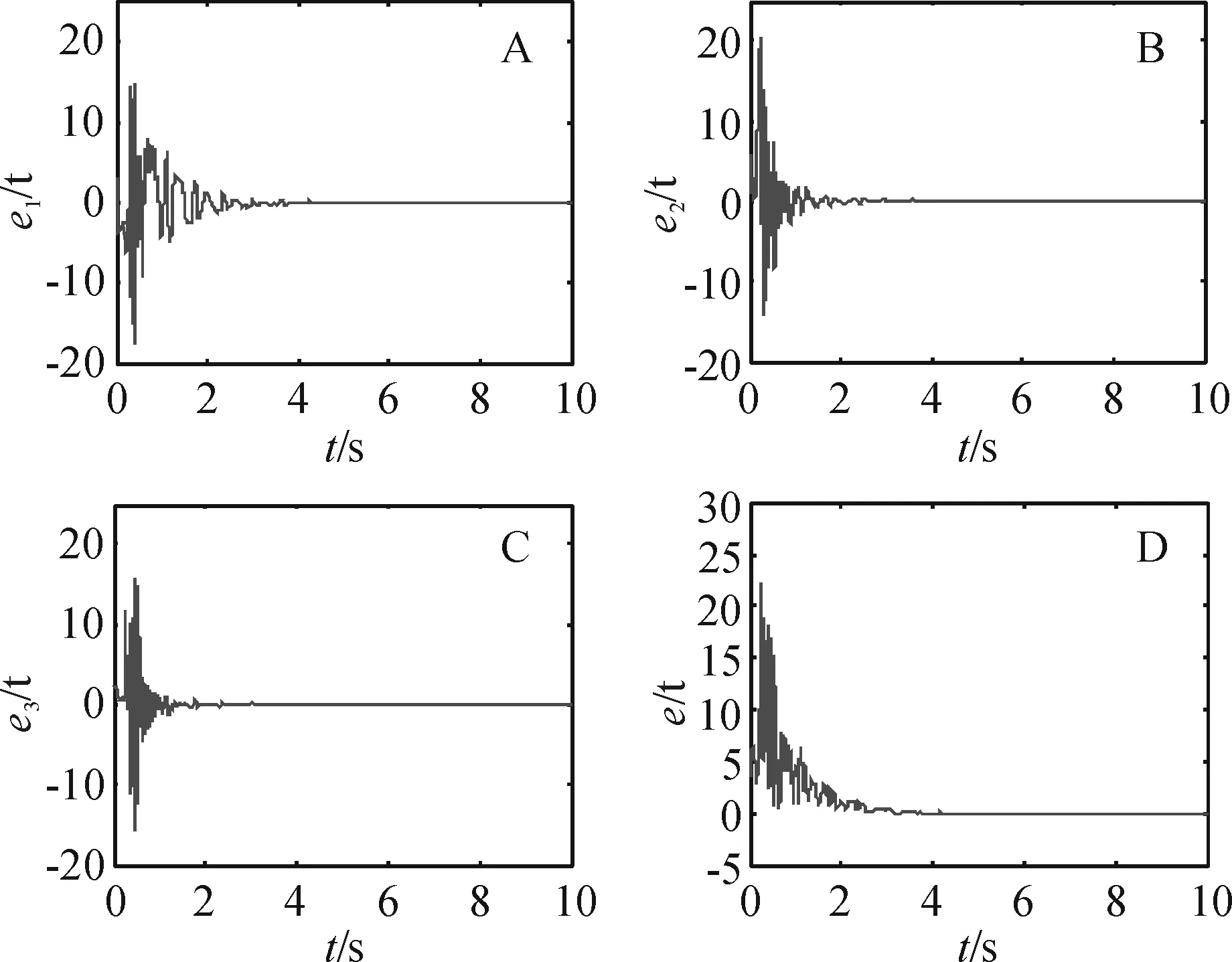

4 结论
