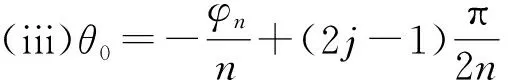与高阶导数分担多项式的整函数
2014-08-28陈敏风陈宗煊
陈敏风, 陈宗煊
(华南师范大学数学科学学院,广州 510631)
1 引言与结果
亚纯函数值分布理论的基本结果和标准记号见文献[1].另外,将使用记号(f)、σ(f)和σ2(f)分别表示亚纯函数f(z)的零点收敛指数、级和超级[2],σ2(f)被定义为
假设f和g是2个非常数亚纯函数,a是一个有限复数.我们说f和g有公共值aCM(IM),假若f-a和g-a有同样的零点并计及重数(忽略重数).我们说f和g有公共值zCM,或说f和g有公共不动点,假若f(z)-z和g(z)-z有同样的零点和同样的重数.
Rubel和Yang[3]首先研究了亚纯函数和它们的导数有公共值问题,得到如下定理.
定理A 假设f是非常数整函数.如果f和f′有2个有限公共值CM,那么f=f′.
如果整函数f和它的导数f′具有一个有限公共值CM,那么f和f′之间的关系将如何?Brück[4]提出了下面猜想.
猜想1 假设f是非常数整函数,其超级σ2(f)<∞且σ2(f)不是正整数.如果f和f′具有有限公共值aCM,那么f′-a=c(f-a),其中c是非零常数.
这个猜想对于a=0和f是有限级的情况分别由Brück[4]、Gundersen和Yang[5]证明,对于f具有无穷级且σ2(f)<1/2的情况由Chen和Shon[6]证明.
亚纯函数具有公共不动点的问题是唯一性理论中的重要问题,文献[7]证明了下面的定理:
定理B 假设f(z)和g(z)是2个非常数亚纯(整)函数,n≥11(n≥6)是正整数.如果fnf′(z)和gng′(z)具有公共值zCM,那么或f(z)=c1ecz2,g(z)=c2e-cz2,其中c1,c2和c是常数,满足4(c1c2)n+1c2=-1,或f(z)≡tg(z),其中t为满足tn+1=1的常数.
陈宗煊和张占亮[8]研究了与Brück猜想对应的整函数与它的高阶导数具有公共不动点的问题,得到下面定理.
定理C 假设f是非常数整函数且满足超级σ2(f)<1/2,k是一正整数.如果f和f(k)具有公共值zCM,那么
f(k)(z)-z=c(f(z)-z),
其中c是非零常数.
本文将考虑整函数与它的高阶导数分担多项式的问题,证明下面的定理.
定理1 假设f是非常数整函数且满足超级σ2(f)<1/2,k是一正整数.如果f和f(k)具有公共值p(z)CM,其中p(z)=amzm+am-1zm-1+…+a0(am≠0,am-1,…,a0均为常数),那么
f(k)(z)-p(z)=c(f(z)-p(z)),
其中c是非零常数.
由定理1可得到下面的推论.
推论1 假设f(z)满足定理1的假设条件.如果存在点z0满足f(k)(z0)=f(z0)≠p(z0),那么f(k)(z)=f(z).
推论2 假设f(z)满足定理1的假设条件.如果存在点z0和一正整数1≤n≤m满足f(k+n)(z0)=f(n)(z0)≠p(n)(z0),那么f(k)(z)=f(z).
推论3 假设f(z)满足定理1的假设条件.如果存在点z0和一正整数n>m满足f(k+n)(z0)=f(n)(z0)≠0,那么f(k)(z)=f(z).
2 相关引理
引理1[9]假设f是无穷级整函数,那么f能被表示成
f(z)=U(z)eV(z),
其中U和V是整函数且满足
(f)=(U)=σ(U),2(f)=2(U)=σ2(U),
σ2(f)=max{σ2(U),σ2(eV(z))},
引理2[10]假设g(z)是无穷级整函数且超级σ2(g)=σ,而v(r)是g(z)的中心指标.那么
类似于文献[11]的证明可得到下面的引理3.

(i)如果σ2(f)=α(0<α<∞),那么
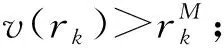
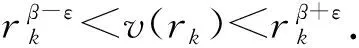
引理4[12]假设
Q(z)=bnzn+bn-1zn-1+…+b0,

那么存在一正数R=R(ε)满足对|z|=r>R,
Re{Q(z)}>αn(1-ε)sin(nε)rn,

Re{Q(z)}<-αn(1-ε)sin(nε)rn,


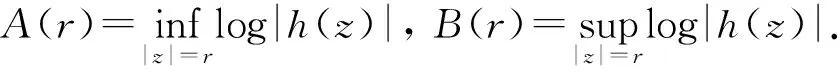
如果σ<α<1,那么


引理6[14]假设h(z)是整函数且下级μ=μ(h)<1/2和μ<σ=σ(h).如果μ≤δ 其中C(σ,δ,α)是仅依赖于σ、δ和α的正常数. 引理7[15]假设f(z)是超越亚纯函数,设α>1是给定常数.那么 (1) 引理9 假设F(z)是整函数,p(z)和Q(z)是非常数多项式,k是一正整数.其中p(z)=amzm+am-1zm-1+…+a0(am≠0,am-1,…,a0均为常数).如果F(z)和Q(z)满足 (2) 或 (3) 或 (4) 那么F(z)具有无穷级. (5) 取 如果Re{Q(z)}>αnθrn,由式(4)可得 (6) 由式(5)和Re{Q(z)}>αnθrn,可知当r→∞时 (7) (8) 由式(6)~(8)可知当r→∞时 |F(reiθ)|→0. (9) 如果Re{Q(z)}<-αnθrn,由式(4)得到 (10) 我们断言在argz=θ上|F(k)(reiθ)|≤2|amm|rm.否则,存在点列{rl}满足 M(rl,F(k)(reiθ),θ)= max{|F(k)(reiθ)|:0≤r≤rl,argz=θ} 和 |F(k)(rleiθ)|=M(rl,F(k)(reiθ),θ)>2|am|rlm. (11) 由于 F(rleiθ)=F(0)+F′(0)rleiθ+…+ 其中0≤|t|≤|t1|≤…≤|tk-1|≤|z|=rl.推导得 |F(rleiθ)|≤|F(0)|+rl|F′(0)|+…+ |F(0)|+rl|F′(0)|+…+ 和 (12) 因此,由于Re{Q(z)}<-αnθrn,由式(11)、(12),得到 (13) 和 (14) 由式(13)、(14)可知式(10)矛盾,表明|F(k)(reiθ)|≤2|am|rm在argz=θ上.所以 |F(reiθ)|≤2|am|rm+k<2|am|r2m(1≤k (15) 在射线argz=θ上. 由引理1可得 (16) 其中Q(z)是整函数,满足σ(Q)=σ2(eQ)<1/2. 下面假设f(z)是超越的.令F(z)=f(z)-p(z),那么由于f(z)是超越的, (17) 由式(16)得到 (18) 其中qk(z)满足如果1≤k (1)Q(z)是常数; (2)Q(z)是多项式且次数degQ=n≥1; (3)Q(z)是超越整函数. 现在分成3种情况来证明. 情况1:Q(z)是常数.定理1成立. 情况2:Q(z)是多项式且次数degQ=n≥1.下面将推导出矛盾. (19) 其中v(r)是F(z)的中心指标.把式(19)代入式(18)得 (20) 由于|F(z)|=M(r,F)和F(z)是超越的,可知 (21) (22) 如果δ=0,则对任意大的M(>0),当rl充分大时,有 (23) 对{zl=rleiθl},由式(20)、(21)和|F(zl)|=M(rl,F),得到 (24) 假设 (25) 由引理4,存在2n个开角域,对上面的ε, 对上面的θ0,存在3种情况: 再分成这3种子情况. (26) 其中d=αn(1-ε)sin(nε)>0.如果δ>0,那么由于3ε<δ、式(22)、(24)和式(26),可得 (27) 易知式(27)矛盾.如果δ=0,那么由式(23)、(24)和式(26),可知 (28) 易知式(28)也是矛盾的. (29) 其中d=αn(1-ε)sin(nε)>0.对{zl=rleiθl},由式(24)和式(29)可得 (30) 由式(30)推导出σ2(F)≥n,这与式(17)矛盾. (31) 或对δ=0,有 (32) 易知式(31)和式(32)都是矛盾的.所以在Ω1内最多有有限个点zl. (33) 由式(33)得到σ2(F)≥n≥1.这与式(17)矛盾.所以在Ω2内最多有有限个点zs. zl=rleiθ0(l>N). (34) 由式(34)和θ0=-φn/n+(2j-1)π/(2n),得到 Re{αneiφn(reiθ0)n}=0. (35) 现在考虑Re{Q(zl)},由式(25)、(35),可知存在2种子情况: 子情况(iii)(a):存在某个s(1≤s≤n-1),满足Re{bn-1(reiθ0)n-1}=…=Re{bs+1(reiθ0)s+1}=0和Re{bs(reiθ0)s}≠0; 子情况(iii)(b):Re{bn-1(reiθ0)n-1}=…=Re{b1(reiθ0)}=0. (36) 或当δ=0时,有 (37) 易知式(36)和式(37)都是矛盾的. (38) 由式(38)得到σ2(F)≥s≥1.这与式(17)矛盾. 对子情况(iii)(b), Re{bn-1(reiθ0)n-1}=…=Re{b1(reiθ0)}=0, 则存在常数M1>0满足-M1 e-M1≤|eQ(rleiθl)|=|eQ(rleiθ0)|≤eM1. (39) 由式(22)(或式(23))、(24)和式(39)得到 |eQ(rleiθl)|≤eM1, (40) 或 |eQ(rleiθl)|≤eM1. (41) 易知式(40)和式(41)都是矛盾的. (42) klogv(r)+O(1). (43) 由引理2有 对充分大的r,由式(43),得到 |Q(z)|≤rσ2(F)+1+O(1). (44) |Q(z)|≥M(r,Q)c, (45) (46) 参考文献: [1] 杨乐. 值分布论及其新研究[M]. 北京: 科学出版社, 1982. [2] 仪洪勋, 杨重骏. 亚纯函数唯一性理论[M]. 北京: 科学出版社, 1995. [3] Rubel L A, Yang C C. Values shared by an entire function and its derivative[M]∥Buckholtz J D,Suffridge T J. Complex analysis. Berlin: Speringer-Verlag, 1977, 599:101-103. [4] Brück R. On entire functions which share one value CM with their frist derivative[J]. Results in Mathematics, 1996, 30: 21-24. [5] Gundersen G, Yang L Z. Entire functions that share one value with one or two of their derivative[J]. Journal of Mathematical Analysis and Applications, 1998, 223: 88-95. [6] Chen Z X, Shon K H. On conjecture of R Brück concerning the entire function sharing one value CM with its derivative[J]. Taiwanese Journal of Mathematics, 2004, 8(2): 235-244. [7] Fang M L, Qiu H L. Meromorphic functions that share fixed-points[J]. Journal of Mathematical Analysis and Applications, 2000, 268: 426-439. [8] 陈宗煊, 张占亮. 与高阶导数有公共不动点的整函数[J]. 数学学报:中文版, 2007, 50(6): 1213-1222. Chen Z X, Zhang Z L. Entire functions sharing fixed points with their higher order derivatives[J]. Acta Mathemtica Sinica: Chinese Series, 2007, 50(6): 1213-1222. [9] Jank G, Volkmann L. Meromorphic function and differential-glaichungen[M].Boston:Birkhauser, 1985. [10] Chen Z X. On the hyper-order of solutions of some second-order linear differential equations[J]. Acta Mathemtica Sinica: English Series, 2002, 18(1): 79-88. [11] Chen Z X. The growth of solutions off″+e-zf′+Q(z)f=0 where the order(Q)=1[J]. Science in China: Series A, 2002, 45: 290-300. [12] Markushevich A I. Theory of functions of a complex variable(Vol 1)[M]. Translated by Silverman R A. Englewood Cliffs, NJ: Prentice-Hall, 1965. [13] Barry P D. On a theorem of besicovitch[J]. The Quarterly Journal of Mathematics, 1963, 14(1): 293-302. [14] Barry P D. Some theorems related to the cosπρtheorem[J]. Proceeding of the London Mathematical Society, 1970, 21: 334-360. [15] Gundersen G. Estimates for the logarithmic derivative of a meromorphic function, plus similar estimates[J]. Journal of the London Mathematical Society, 1988, 37(2): 88-104. [16] 何育赞, 萧修治. 代数体函数与常微分方程[M]. 北京: 科学出版社, 1988.






3 定理1的证明