基于estk-Berggren公式的动态固化动力学模型的非线性回归分析

左路,夏兰君

(湖北大学化学化工学院,湖北 武汉 430062)

基于estk-Berggren公式的动态固化动力学模型的非线性回归分析

左路,夏兰君

(湖北大学化学化工学院,湖北 武汉 430062)

动态自催化固化反应动力学研究中的机理函数基于SB公式,动力学模型需要拟合4个参数:指前因子A、活化能Ea、反应阶数m、n.本文中采用非线性最小二乘回归方法,拟合结果表明4个参数的非线性回归结果不稳定,尤其表现在参数A与m的估计结果上.笔者对造成上述结果的原因进行了分析,指出由于模型参数效应曲率相当大,增加了模型的非线性强度,使得最小二乘回归分析结果不可靠.根据实验数据特征,本文中在不确定机理函数形式前提下,运用Model-free方法,先获得活化能平均意义下的估计值,再进行参数A、m、n的非线性最小二乘回归分析.结果表明减少回归函数参数个数,可极大程度降低模型的非线性强度,从而获得有效的动力学参数估计.

化学动力学;非线性回归分析;非线性强度;曲率

0 引言

化学动力学从动态角度观察化学反应,研究反应对时间与温度等因素的依赖性,建立解释这种依赖的经验模型,通过实验数据获得模型参数来描述动力学特性.这种方法快速便捷,利用适当的动力学模型从现象角度量化反应特征,化学反应机理研究则退居其次.实际应用中,通过差式扫描量热分析法(differential scanning calorimeter,以下简称DSC),获得动态(非等温)条件,或者等温条件下自催化固化反应实验数据,对反应动力学模型进行回归分析,从而得到描述反应动力学特征的动力学参数.实验中扫描不同升温速率下(动态反应时)或者不同温度时(等温反应时)反应热流值,获得热流-时间曲线,热流曲线与基线间面积为整个反应热量值ΔHtotal.将时刻t扫描的热流值与整个反应热流值求比值得到该时刻的反应固化程度α(=ΔHt/ΔHtotal),α是时间t的函数α(t),取值于0≤α(t)≤1,在反应初始阶段α(t0)=0.

根据实验温度条件,动力学研究分为等温与动态方式,等温法相对于动态法具有可靠性强的优点,但是实验耗时长,且存在零时间效应,从上世纪60年代开始在动态过程中开展快速动力学研究.动态实验中,温度按照线性、双曲型、似等温型、任意型等控制程序以一定速率上升,对整个反应温度范围进行热流扫描,可以获得大量不同温度下的动力学信息.动态法获得反应动力学参数虽经过长期发展和研究,但是大量文献给出的各种环境、各种反应机理获得的动力学参数有着显著不同[1,3],存在参数不稳定、不可靠现象[4].造成这种现象的原因即有来自实验的误差因素、模型假定差异,也有数据处理方法等因素.本文中将对动态下自催化固化实验DSC数据进行非线性回归分析,从动力学模型特征上探讨造成上述差异的原因.

1 模型描述与数据预处理

动态动力学分析过程建立于基本速率方程dα/dt=k(T)f(α)[5]之上,dα/dt表示固化速率,k(T)为依赖绝对温度T的Arrhenius速率常数,f(α)是依赖于固化度α的反应机理函数(微分形式).不同反应机理下,f(α)具有不同的形式(表1).1971年estk与Berggren(以下简称SB)将反应机理函数描述为三参数形式f(α)=αa(1-α)b(-ln(1-α))p[6],SB公式源自于S形人口增长模型的Logistic函数[7],适用于广泛的动力学分析.1980年Gorbachev将公式简化为自催化反应的两参数形式f(α)=αm(1-α)n[8],αm描述反应结束或者产物形成规律,另一部分(1-α)n描述反应中的自催化效应. 这两部分作用相互抵消又相互依赖,指数m、n取值非负值,在m≤1时模型才有实际意义,指数n(>1)值与反应复杂程度成正比.

根据Arrhenius方程[9],反应速率常数为具有负指数的指数函数k(T)=Ae-Ea/RT,其中参数A为指前因子(s-1),Ea表示活化能(J/(mol-1·K-1)),R表示气体常数(=8.314J·K-1·mol-1). 将Arrhenius方程引入速率方程,得到动态动力学模型为

dα/dt=Ae-Ea/RTαm(1-α)n

(1)

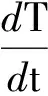
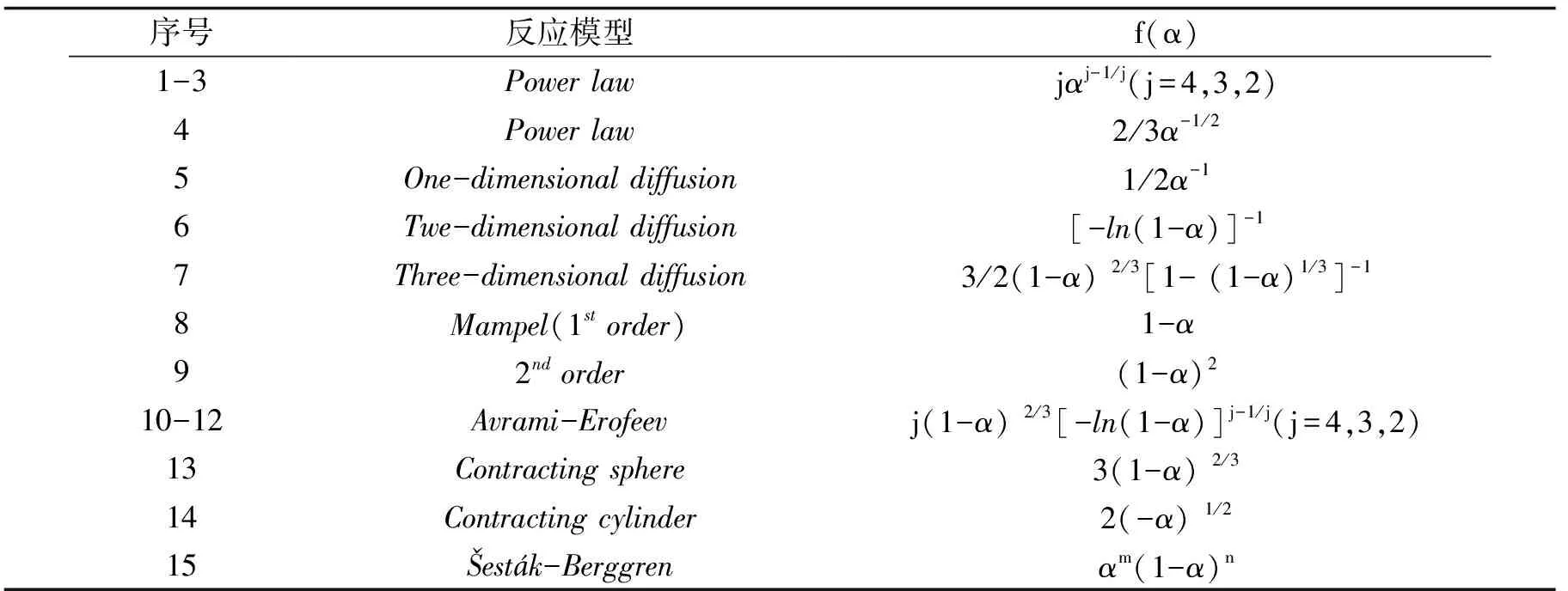
表1 反应机理函数

在升温速率分别为5、10、12.5、15、20 ℃/min时,通过DSC法得到实验数据(T,α,dα/dt)(见图1-图2),图1所示固化度-温度关系图呈现出典型的S形态.非线性最小二乘法进行回归分析时,拟合算法需要计算模型函数对估计参数的偏导数,其中偏导数∂f/∂m,∂f/∂n表达式中将分别出现对数函数lnα与ln(1-α),因此当α取值为0或者1时,将导致该偏导数无意义,拟合过程无法进行.因此,剔除实验数据中α为0或1的数据点,再利用其余数据点进行拟合. 本文中回归分析计算环境为美国WolframResearch公司的计算软件Mathematica,其强大的计算功能通过符号计算语言来实现,Mathematica从1988年第一版发布便标志着现代科学计算的开端.Mathematica在非线性回归的大样本数据处理中具有稳定、快速、精度高的优势,并且能够胜任回归模型非线性强度分析的复杂计算.

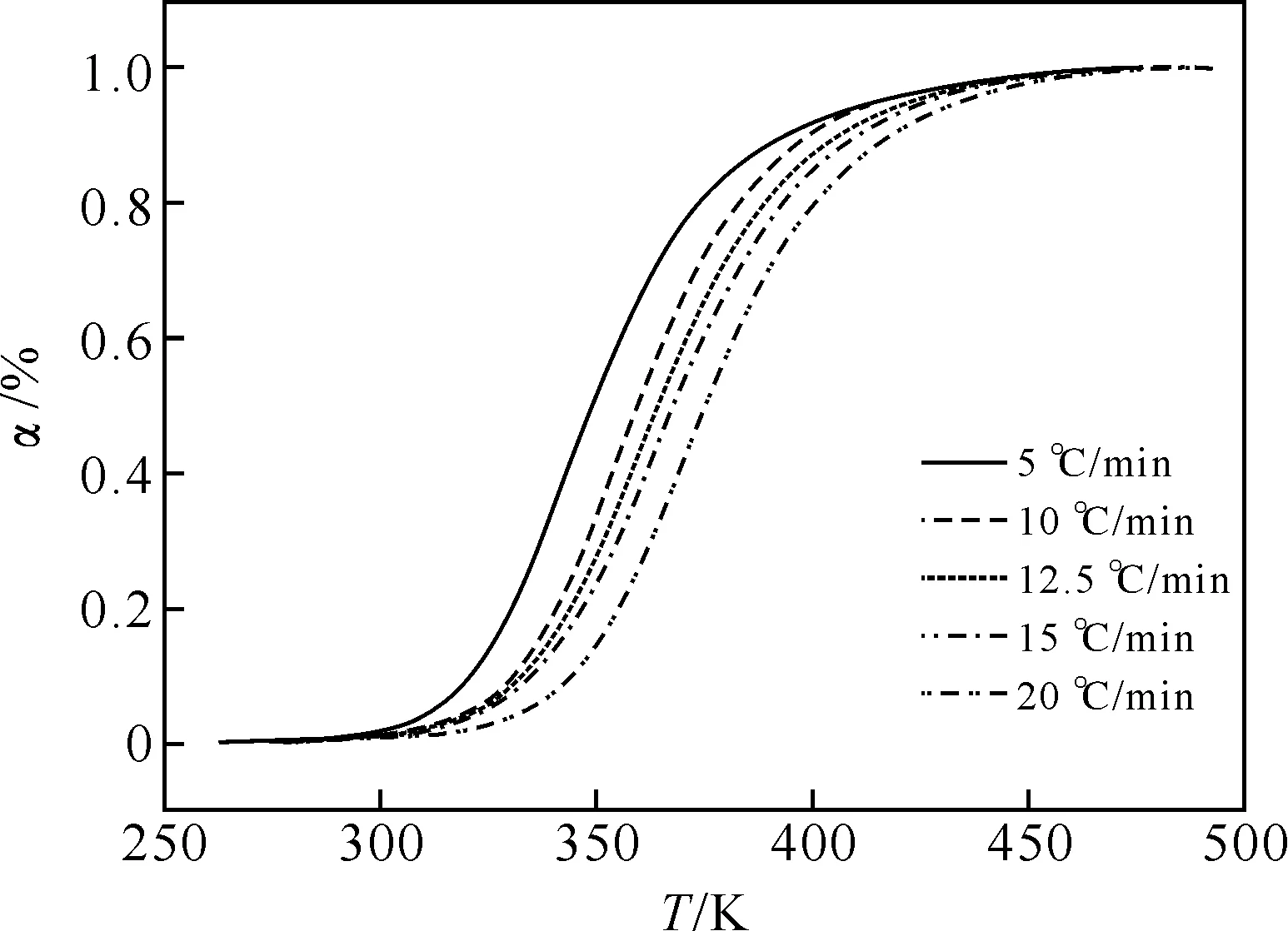
图1 不同升温速率下α-T图

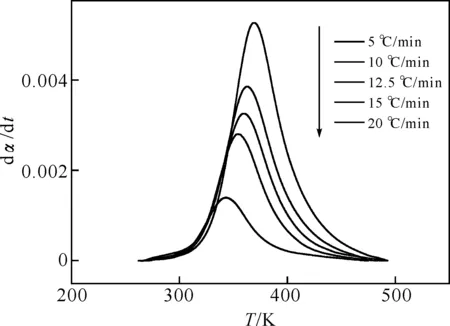
图2 不同升温速率下dα/dt-T图

2 模型的非线性回归分析

非线性回归的最小二乘法算法利用一阶泰勒展开式线性近似回归函数,并将此线性近似作为回归函数进行最小二乘回归分析.模型(1)的泰勒展开式略去增量Δi的二次及其以上的高次项,得到如下近似形式

(2)

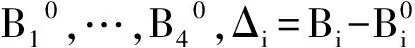
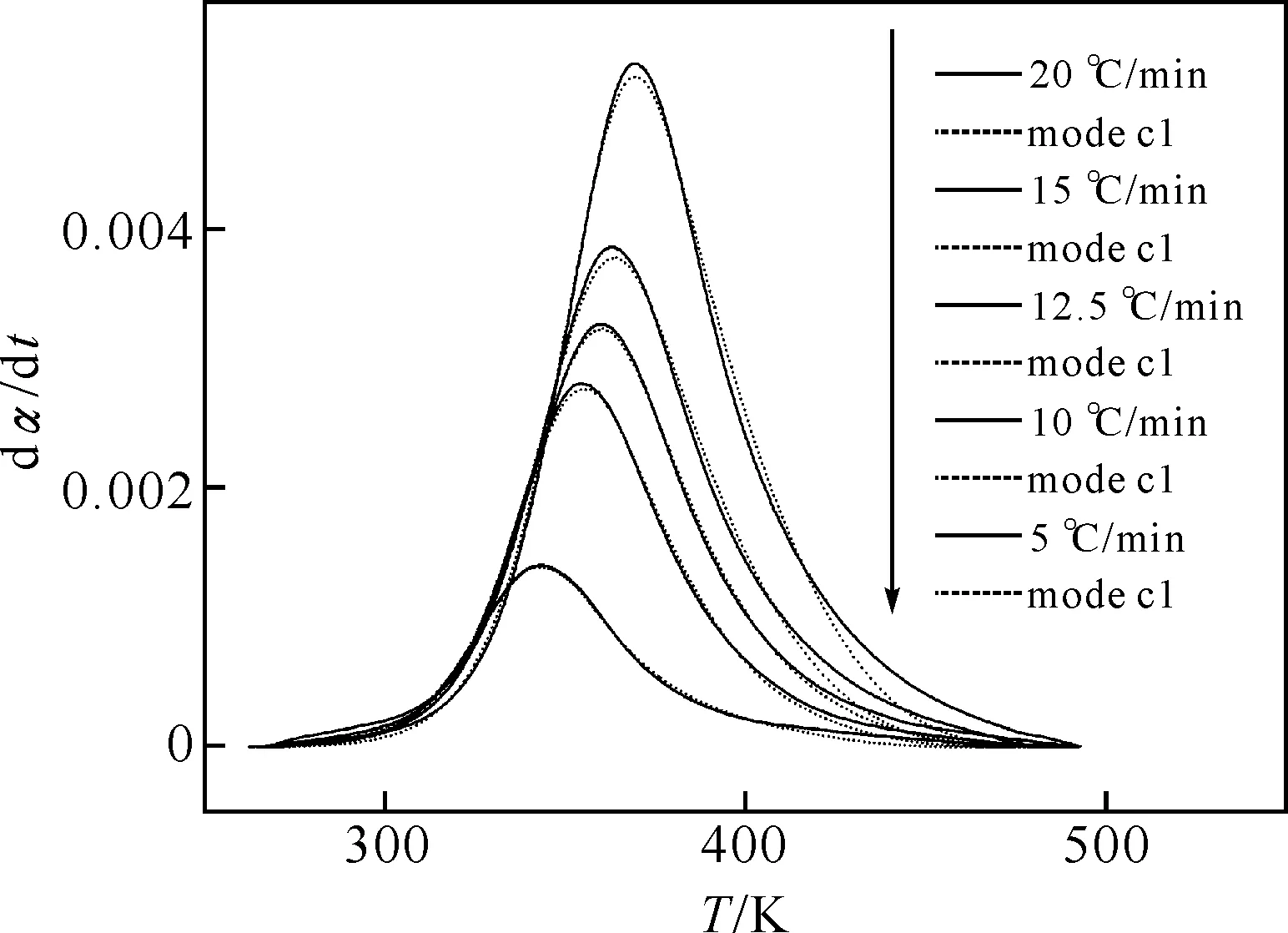
图3 模型(1)拟合结果图

2.1 4个参数的非线性拟合Mathematica中通过NonlinearModelFit函数,并采用最小二乘Levenberg-Marquardt法进行非线性拟合,Levenberg-Marquardt法是改良后的Gauss-Newton法,引入迭代阻尼因子修正了Gauss-Newton法可能存在的不收敛性.Levenberg-Marquardt法的迭代过程需要参数的初始值信息,并且对初始值的依赖性非常强,最大迭代次数的限制也会影响到最终的结果.参考文献 [11]中A,Ea,m,n的估计值,本文中选择分别用2.0×105(1/s)、40 000J/mol、0.2、1作为参数A,Ea,m,n的初始值,并设置迭代最大次数为500,拟合结果如表3和表4所示,曲线拟合结果比较见图3.除了反应后期阶段有偏差,所有升温速率下的回归结果与实验数据很好的拟合.这是因为反应到了一定阶段,反应过程还受到了扩散作用的控制,模型(1)中没有描述扩散因子.

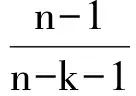
表3和表4中拟合的Adj-R2值均>0.99,与图3的拟合效果吻合.但是观察参数拟合效果发现A与m的估计值显示出很大的波动性,并且标准误差与估计值的比例分别为60%,95%,95%置信区间跨越0值,且区间长度达到估计值的2倍以上,估计结果失去了价值.

2.2模型非线性强度的度量最小二乘Levenberg-Marquardt法拟合实际是一种线性近似方法,估计效果的优劣与非线性模型有着密切的关系.Beale[12]在1960年提出了度量非线性模型的线性近似在统计推断上优劣程度的数量指标,即非线性强度的度量——曲率.Bates与Watts[13]将Beale的概念分解为固有曲率、参数效应曲率,并建立比较标准——相对曲率值,通过固有曲率、参数效应曲率与相对曲率的大小关系来判断回归模型的非线性强度.固有曲率大小反映了期望平面的平坦程度,期望平面越平坦,越可以用切平面去近似,近似效果越好.因此期望平面越平坦,固有曲率就越小.参数效应曲率则反映模型参数对于非线性程度的贡献值,若固有曲率、参数效应曲率均小于相对曲率值,那么对于非线性模型的线性近似具有可行性,并对其进行最小二乘法的回归分析结果可以接受;固有曲率大于相对曲率值时,说明模型的固有非线性非常强,不适合采用线性近似方法进行拟合,在实用上,模型的固有非线性往往可以忽略不计[14];参数效应曲率大于相对曲率值时,说明模型的非线性特征主要由参数造成,需要对参数进行变换,修正模型再进行回归分析.

模型(1)的曲率如表5所示,每个升温速率下模型的相对曲率一致,固有曲率、最大参数效应曲率随升温速率增加呈上升趋势.由于实验中每秒扫描一次以获得热流量数据,当升温速率低时,反应持续时间长,获得的数据信息丰富,因此参数效应曲率随着升温速率增加而上升.每个升温速率下,固有曲率远小于相对曲率,表明模型自身的固有非线性程度可以忽略不计,但是由于参数效应曲率极大程度超过了相对曲率,说明该模型的非线性特征主要受到参数的影响,因此希望通过参数变换或者减少模型(1)的参数个数降低参数效应曲率.

2.3三个参数的非线性拟合观察图2,我们会发现dα/dt曲线随着温度T的升高,有单一峰值出现.

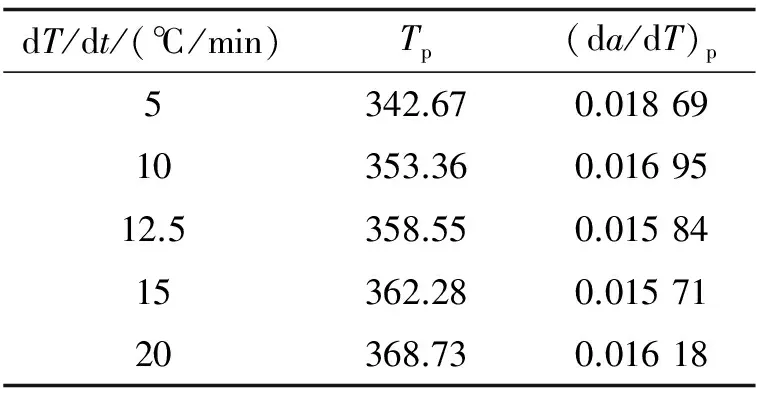
表2 不同升温速率下(da/dT)p,Tp值

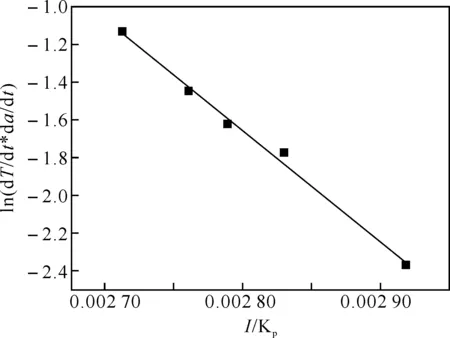
图4 Friedman法求活化能线性拟合图

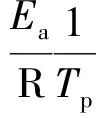
dα/dt=Ae-48 960.15/RTαm(1-α)n

(3)

在不同升温速率下重新拟合得到参数(表4中模型(3))与模型的非线性曲率值(表5中模型(3)),Adj-R2几乎没有变化,但是参数A,m,n的值随着升温速率的升高呈现出下降的趋势,并且标准误差比模型(1)的估计结果缩小10-1,置信区间更短且没有跨越0值. 模型(3)的相对曲率略有减小,固有曲率缩小10-1,参数效应曲率缩小10-4～10-5,并且两者均小于相对曲率,减少参数个数极大程度降低了模型的非线性程度,此时再进行的线性近似的最小二乘法是有效且可行的.

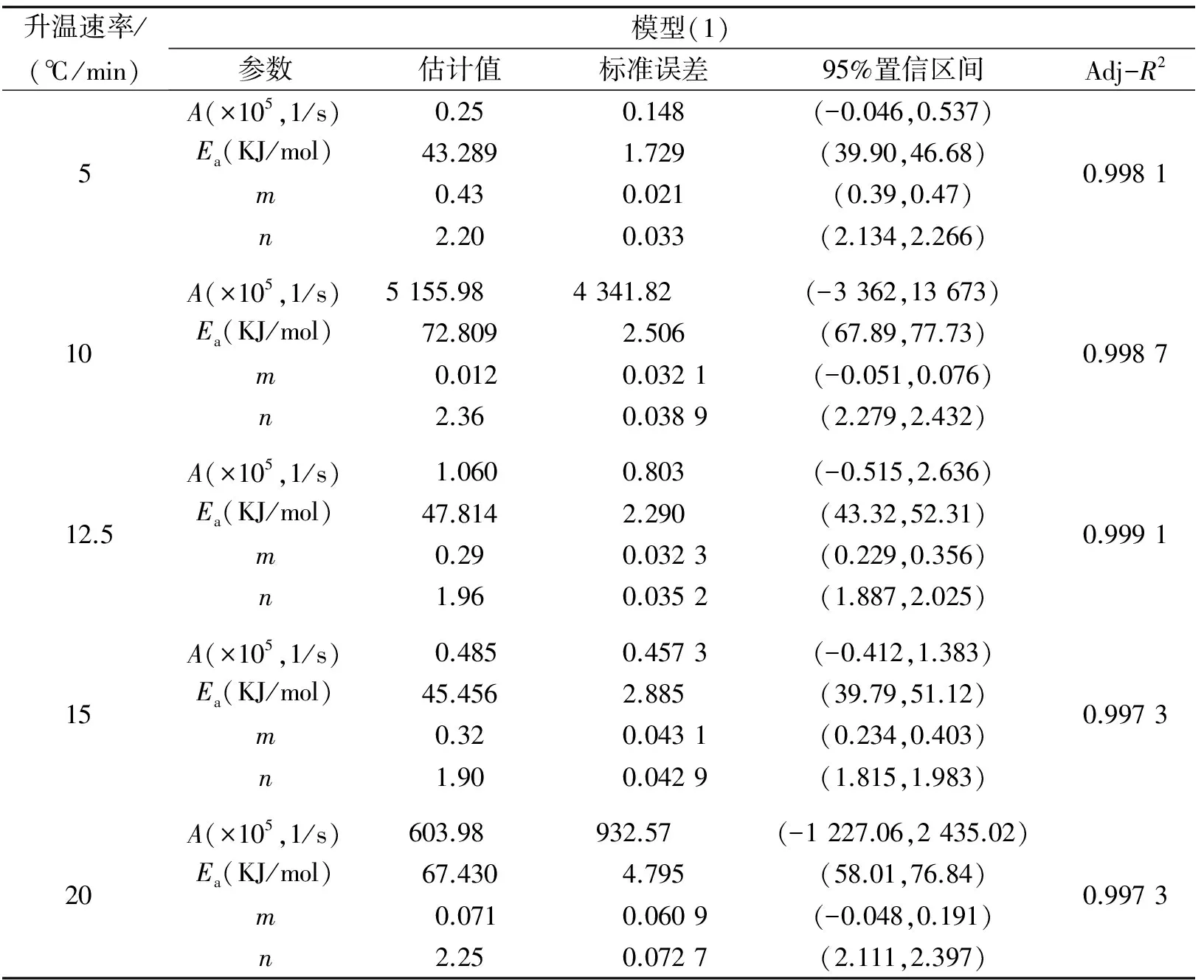
表3 模型(1)的非线性拟合结果

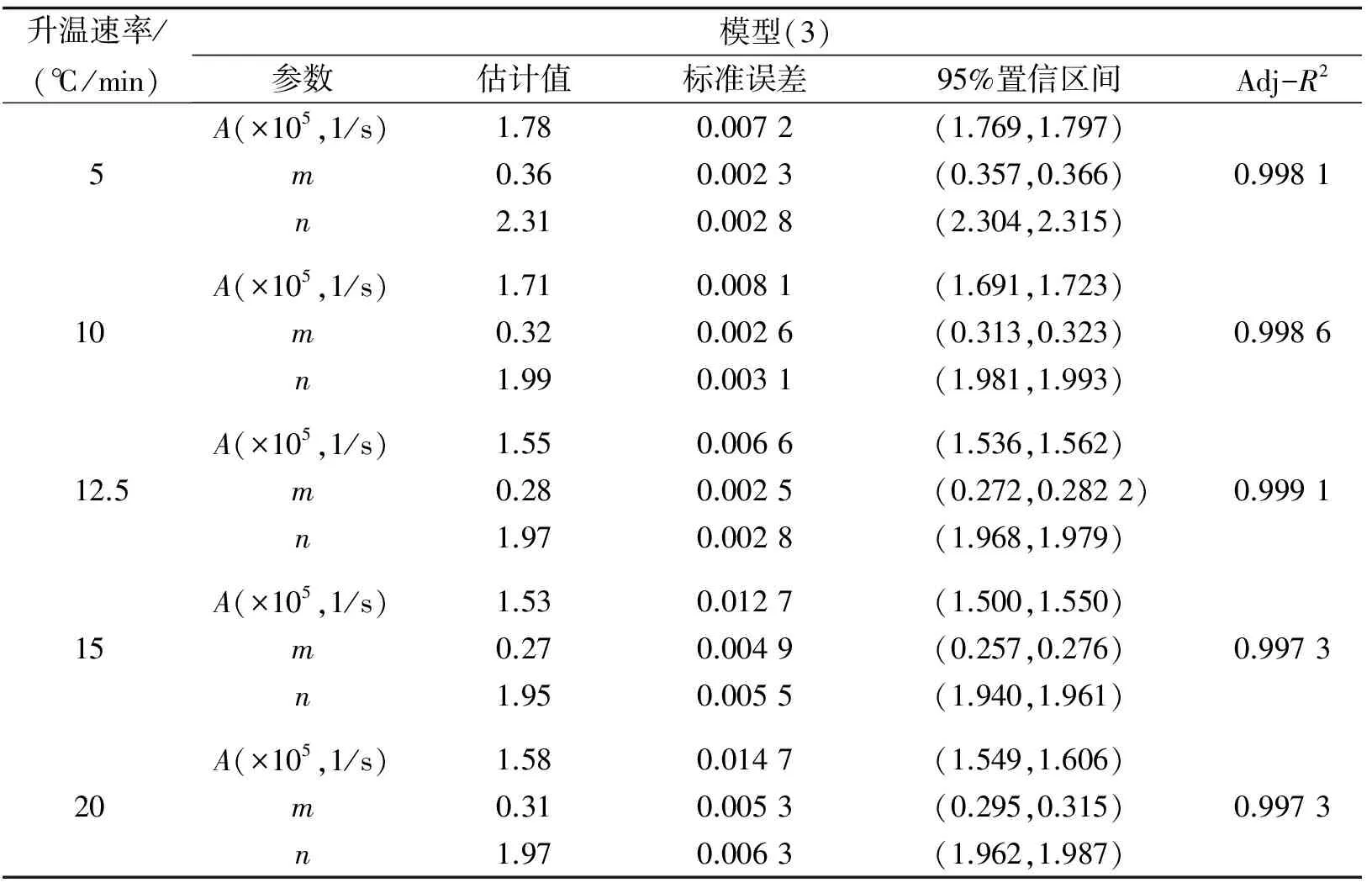
表4 模型(3)的非线性拟合结果

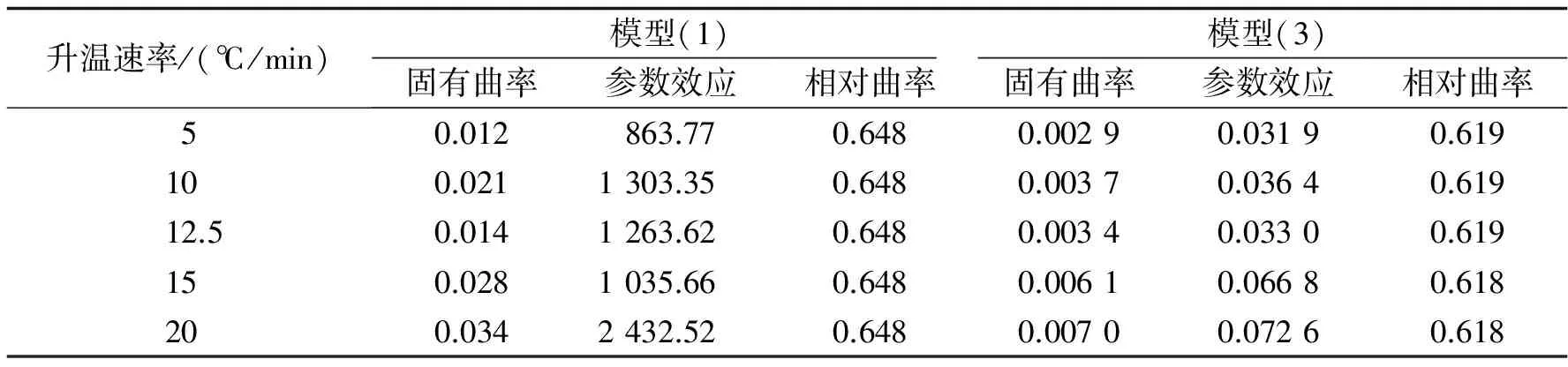
表5 不同升温速率下模型(1)、(3)的曲率

3 结论

动态条件下的快速动力学研究提供了较等温条件下温度范围广泛的反应信息,但是动力学模型也因此引入了新的变量.基于SB公式的自催化反应机理函数由两个参数决定,模型的复杂程度因此增加,影响了非线性回归中参数A、Ea、m、n的估计值.回归模型是温度和固化度的非线性函数,其非线性强度程度大小将影响回归分析结果的有效性.模型参数效应曲率大于相对曲率时,就要考虑对参数进行变换,通过峰值等数据特殊点值预先确定某些参数值,减少回归模型参数个数,改善拟合模型的非线性性态,利用最小二乘法得到的回归结果提供有价值的动力学特征参数值.

[1] Sergey V, Charles A W. Model-free and model-fitting approaches to kinetic analysis of isothermal and nonisothermal data[J]. Thermochimica Acta,1999(340/341):53-68.

[2] Omar Moussa, Anastasios P Vassilopoulos, Thomas Keller. Effects of low-temperature curing on physical behaviors of cold-curing epoxy adhesives in bridge construction[J]. International Journal of Adhesion & Adhesives,2012(32):15-22.

[3] Nicolas Sbirrazzuoli. Determination of pre-exponential factors and of the mathematical functionsf(α) ofG(α) that describe the reaction mechanism in a model-free way[J]. Thermochimica Acta,2013(564):59-69.

[4] 葛庆仁.非等温气固反应动力学曲线非线性拟合求解[J].中国核科技报告,1987(S1).

[5] Brown M E, Dollimore D, Galwey A K. Reactions in the solid state[J]. Comprehensive Chemical Kinetics,1980:22.

[8] Gorbachev V M. Some aspects ofestk’s generalized kinetic equation in thermal analysis[J]. J Therm Anal,1980,18:193-197.

[9] Arrhenius S. On the reaction rate of the inversion of non-refined sugar upon souring[J]. Z Phys Chem,1889(4):226-248.

[10] Macro Schwaab, José Carlo Pinto. Optimum reference temperature for reparameterization of the Arrhenius equation, Part 1: Problems involving one kinetic constant[J]. Chemical Engineering Science,2007(62):2750-2764.

[11] Sun L, Pang S, Sterling A, et al. Dynamic analysis of curing process of Epoxy Prepeg[J]. J Appl Polym Sci,2002,86(8):1911-23.

[12] Beale E M L. Confidence region in nonlinear estimation[J]. J R Statist Soc B,1960;22:41-88.

[13] Douglas M Bates, Donald G Watts. Nonlinear regression analysis and its applications[M].New York: John Wiley & Sons Inc.,1988:232-267.

[14] 韦博成.近代非线性回归分析[M].南京:东南大学出版社,1989:35-93.

[15] Henry L. Friedman. New methods for evaluating kinetic parameters from thermal analysis data[J]. Journal of Polymer Science Part B: Polymer Letters,1969;7:41-46.

(责任编辑 胡小洋)

Regression analysis of non-isothermal cure reaction kinetic model based onestk-Berggren equation

ZUO Lu,XIA Lanjun

(School of Chemistry & Chemical Engineering, Hubei University, Wuhan 430062, China)

In chemical kinetic analysis of non-isothermal cure reaction, autocatalytic reaction mechanism function was based onestk-Berggren equation, parameters of regression were pre-exponential factor A, activation energyEa, reaction ordermandn. In this article, we fit rate equation with four parameters by nonlinear regression based on the least squares estimation, regression result was unreliable, especially the estimator ofAandm. This article pointed that nonlinearity of model with large parameter-effects curvature was responsible for the terrible regression result. In the next section, according to characters of experiment data, we estimatedEafirstly with model-free methods, rate equation would only have three parameters, parameter-effects curvature of model was cut short, and with this solution we could get effective estimation of kinetic parameters.

chemical kinetic; nonlinear regression analysis; nonlinearity; curvature

2013-08-05

左路(1975-),讲师,E-mail:zlumail@hubu.edu.cn

1000-2375(2014)03-0224-06

TQ018;O643.11

A

10.3969/j.issn.1000-2375.2014.03.008