6 072阶单群同构于PSL(2,23)的初等群论证明
2014-03-27周峰徐涛刘合国
周峰,徐涛,刘合国
(湖北大学数学与统计学学院,湖北武汉430062)
本文中采用的符号和术语都是标准的,见文献[1-2].
我们知道,单群在群论里具有基本的重要性.一个单群通常可由它的数量特征(比如群的阶和元的阶的集合)来刻画.运用Sylow定理不难证明60阶单群同构于A5≅PSL(2,5)[1,3],Smith[1]和Huppert[3]分别用群论的不同方法证明了168阶单群同构于PSL(2,7).Isaacs[4]用特征标的理论证明了360阶单群同构于A6≅PSL(2,9),对这个看似简单的结果至今还没有见到纯粹的群论证明.值得指出的是,Rotman[5]希望运用初等群论证明360阶单群同构于A6,但他给出的提示“360阶单群只有6个Sylow 5-子群”是错误的,因为360阶单群的Sylow 5-子群的个数一定是36.在本文中,我们运用初等群论的方法证明了下面的结果.
定理 6 072阶单群同构于PSL(2,23).
定理的证明 设G为6 072阶单群,此时|G|=6 072=23·3·11·23.
首先证明G的Sylow 23-子群的个数n23(G)=24,Sylow 11-子群的个数n11(G)=276.设P是G的Sylow 23-子群,由Sylow定理知n23(G)≡1(mod 23)和n23(G)=|G∶NG(P)|,因此n23=1或24.注意到G是单群,于是n23(G)=24,进而,下证|NG(P)|=253=11·23.下证NG(P)包含23个Sylow 11-子群,根据Sylow定理得到n11(NG(P))=1或23.若NG(P)只有1个Sylow 11-子群Q,则Q◁NG(P),从而NG(P)⊆NG(Q),即有|G∶NG(Q)|整除|G∶NG(P)|=24,因为n11(G)=1(mod 11),所以n11(G)≠24,即|G∶NG(Q)|≤12,因此得到整除12!,矛盾.因此NG(P)包含23个Sylow 11-子群.根据Sylow定理得到G的Sylow 11-子群的个数n11(G)=1,12,23或276.由G是单群可以得到n11(G)≠1或12,若n11(G)=23,则NG(P)包含G的全部Sylow 11-子群,而NG(P)可由这些Sylow11-子群生成,这将有NG(P)◁G,矛盾于G是单群,所以n11(G)=276.
考虑G在Syl23(G)上的共轭作用.由于n23(G)=24,可设
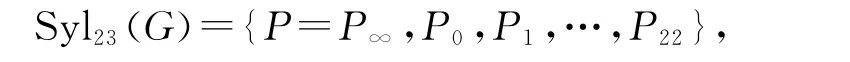
并用{∞,GF(23)}表示被置换的数码集合.设P=<u>,则u∈NG(P∞),所以u保持P∞不动.因为u∉NG(Pi)(0≤i≤22),所以u变动了GF(23)的每个元,因为u是G的一个23阶元,适当调整数码的排列顺序,u共轭作用在Syl23(G)上引起的置换总可以写成(∞)(0,1,2,…,22)的形式.显然u对应的映射为x→x+1,其中x∈{∞,GF(23)},这是一个线性分式映射.
设NG(P)=<u,n>,其中u是一个23阶元,n是一个11阶元.n∈NG(P),故n保持P∞不动.因为211≡1(mod23),所以对所有的x∈GF(11),n对应的映射为x→2x,这是一个线性分式映射.
设N=<n>是G的一个Sylow 11-子群,记H:=NG(N),则|G∶H|=n11(G)=276,从而|H|=22=2·11,于是H有一个2阶元t.由于N◁H,t共轭作用在N上,诱导了N的一个自同构,注意到t为2阶元,因此nt=n或nt=n-1.
若nt=n,则n与t可交换,nt是一个22阶元,即H含有22阶元,此时H是循环群,所以G的所有Sylow 11-子群Ni(1≤i≤276)的正规化子Hi都是循环群,且Hi≠Hj当且仅当NG(Ni)≠NG(Nj)(1≤i,j≤276).Hi含有φ(22)=10(φ为欧拉函数)个22阶元,而G含有276个Sylow 11-子群,因此所有正规化子共含有10·276=2 760个22阶元.
根据Sylow定理可以得到G的Sylow 3-子群的个数n3(G)=1,4,22,46,184或253.注意到G是单群,容易验证n3(G)≠1,4或22.若n3(G)≥46,则G至少有2·46=92个3阶元.因为n23(G)=24,所以G有22·24=528个23阶元,又n11(G)=276,故G有10·276=2 760个11阶元.综上我们得到G中22阶元、3阶元、23阶元和11阶元的总数至少有2 760+92+528+2 760=6 140个,而6 140>6 072=|G|,矛盾.因此nt=n-1.
下证t在{∞,GF(23)}上引起的置换为
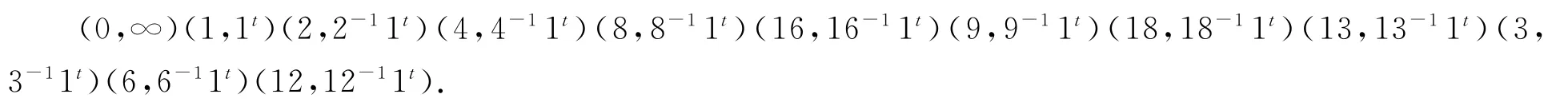
因为G在{∞,GF(23)}上传递,任意一个点的稳定子群阶为253,t为2阶元,所以t没有不动点,因此t对换n的不动点0和∞.由nt=n-1和xn=2x可得(2x)t=xnt=xtn-1,又xn-1=2-1x,故xtn-1=2-1xt,从而(2x)t=2-1xt.在等式(2x)t=2-1xt中我们分别取x=1,2,22,…,29,可以得到置换
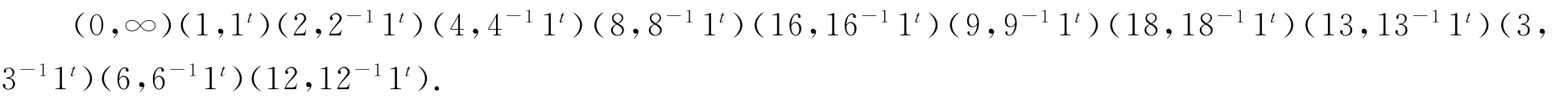
显然t对应的映射为x→x-11t,其中x∈{∞,GF(23)},这是一个线性分式映射.
综上所述,找到了G里的3个元素u:x→x+1,n:x=2x,t:x→x-11t,其中x∈{∞,GF(23)}.容易验证detu=1和detn=2,而GF(23)中的平方剩余为1,2,3,4,6,8,9,12,13,16和18.所以detu和detn是GF(23)中的平方剩余.下证1t不是GF(23)中的平方剩余.由于t在{∞,GF(23)}上引起的置换为
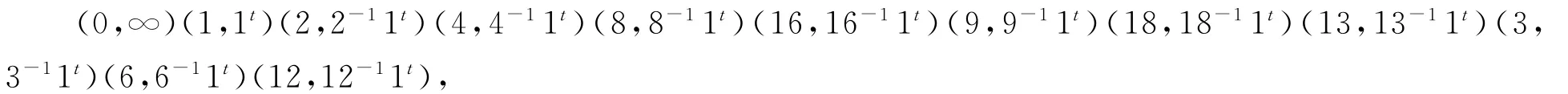
t没有不动点,故

进而

这表明1t不是GF(23)中的平方剩余.又-1不是GF(23)中的平方剩余,于是根据两个非平方剩余的乘积是平方剩余,得到dett=-1t是GF(23)中的平方剩余.因

容易看到u,n,t对应的线性分式映射属于PSL(2,23).
令A=<u,n,t>,其中u,n,t分别是23阶元,11阶元,2阶元.因为2·11·23=506整除|A|,所以|G∶A|≤12.注意到G是单群,于是G=A.故G同构于PSL(2,23)的一个子群,而,因此G≅PSL(2,23).
[1]Smith G,Tabachnikova O.Topics in group theory[M].Berlin:Springer-Verlag,2000.
[2]Isaacs I M.Finite group theory[M].Providence:American Mathematical Society,2008.
[3]B.Huppert.Enliche gruppen I[M].New York:Springer-Verlag,1967.
[4]Isaacs I M.Character theory of finite groups[M].New York:Academic Press,1976.
[5]Rotman J.An introduction to the theory of groups[M].New York:Springer-Verlag,1994.
