鸭式布局双旋弹飞行动力学建模与仿真

常思江,王中原,刘铁铮

(1.南京理工大学 能源与动力工程学院,南京 210094;2.中国兵器科学研究院 军贸装备发展部,北京 100089)

随着低间接伤害概率和高精度打击逐渐成为现代战争对弹药武器的基本要求,弹药应具有精确制导控制的能力。对此,常规弹药的制导化改造是一条颇具吸引力的低成本途径。在常规弹药中,旋转稳定弹是各国大量装备并经常使用的,近年来不少国家对其开展了弹道控制方面的研究。旋转稳定弹绕其纵轴高速旋转以保持稳定飞行,这给弹道控制带来了极大的困难。现有的用于旋转稳定弹的控制机构主要包括增阻机构[1]、减旋机构[2]及脉冲发动机[3]等,这些机构的应用避开了弹体高旋这一难点,但由于其工作状态是离散和有限次的,故这些有控旋转稳定弹还难以满足精确打击的要求。

目前,一种鸭式布局双旋弹成为极具发展潜力的有控旋转弹,如图1所示,其由前体(装有鸭舵)和后体两部分组成,二者间采用滚动轴承连接,在飞行过程中可分别以低速(每秒十几转)和高速(每秒几百转)绕弹体纵轴旋转,故谓之“双旋”。此种结构旨在克服弹体高速自旋给弹道控制带来的固有困难。

图1 鸭式布局双旋弹结构示意图

早在20世纪70年代,Widmayer R S[4]就提出了双旋弹的概念,并从工程角度进行了初步探索;Costello M等[5]对无控双旋弹的弹道模型和飞行特性进行了分析;德法研究所的Wernert P等[6-8]针对头部引信与后弹体滚转解耦的有控旋转弹进行了气动特性分析、稳定性分析及控制系统设计等一系列的初步研究。国内最早是由一些引信方面的专家、学者通过消化、吸收国外技术资料,提出在旋转稳定弹上发展二维弹道修正引信,由此开展了关于减旋装置[9]、修正能力[10]、气动特性数值模拟[11-12]等方面的初步研究。

由于双旋弹转速特性与常规旋转弹的差异较大,有必要建立合理的飞行动力学模型,并描述两体差动自旋、鸭舵控制等条件下的弹道变化规律,这有助于控制方案的设计。上述国外文献偏重于研究结果,分析过程不详甚至有不合理之处,而国内文献在弹道特性描述方面还不是很深入。对此,本文拟从飞行原理入手,在我国外弹道理论体系[13]下,详细讨论鸭式布局双旋弹的飞行动力学建模并进行仿真分析,以期为我国今后研制该类弹箭提供必要的理论依据。

1 飞行原理

在身管中未发射时,弹丸舵面折叠在前体控制舱内,全弹外表与普通旋转弹无异。当发射出炮口后,舵面暂不张开,飞行时前、后体可形成差动自旋,前体转速衰减快于后体。当弹丸飞行进入预定区域后,鸭舵张开,增大了前体的滚转阻尼力矩,使其转速衰减进一步加大,很快达到一较低水平,而后体几乎不受影响,仍可保持较高转速以维持陀螺稳定。如能合理设计前、后体参数(如质量、转动惯量等),弹丸可在“双旋”条件下保持飞行稳定,同时前体转速低,易于采用鸭舵实现较精确的弹道控制。

由于前、后体之间存在差动滚转,在六自由度刚体运动基础上增加了一个自由度,因此必须建立七自由度刚体动力学模型。

2 飞行动力学模型

2.1 坐标系

除外弹道学中常用的弹体坐标系、弹轴坐标系及速度坐标系等[13],对前、后弹体还应分别建立前体坐标系ox1y1Fz1F和后体坐标系ox1y1Az1A,如图2所示。

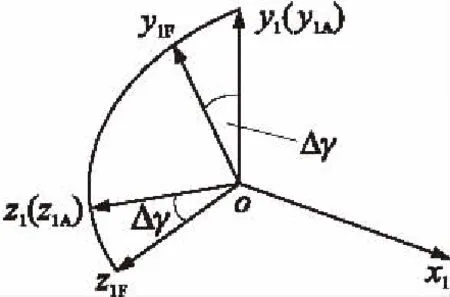
图2 前体坐标系和后体坐标系

后体坐标系ox1y1Az1A与常规的弹体坐标系ox1y1z1是重合的,而前体坐标系ox1y1Fz1F则是在后体坐标系基础上将oy1A轴绕ox1轴转过角度Δγ得到,Δγ为差动滚转角。根据此定义,有

Δγ=γF-γA

(1)

式中:γF,γA分别为前体和后体的滚转角;γA与弹体滚转角γ相同。

2.2 质心运动方程

鸭式布局双旋弹采用鸭舵控制,故可在速度坐标系中建立质心动力学方程:

式中:t为飞行时间;m为弹体质量;v为速度;θa为弹道倾角;ψ2为弹道偏角;Fx2,Fy2,Fz2为除控制力外的合外力在速度坐标系中的分量;Fc,x2,Fc,y2,Fc,z2分别为鸭舵控制力在速度坐标系中的分量;弹箭无控飞行时k=0,有控飞行时k=1。

由于方程中不显含弹丸的姿态运动参数,故质心运动学方程与普通旋转弹质心运动学方程[13]形式上是完全相同的。

2.3 绕质心运动方程

式中:Jy,F,Jx,F分别为前体对其自身惯性主轴的赤道转动惯量和极转动惯量。后体转动惯量表达式类似,只需将下标由F换成A。

根据动量矩定理,有

式中:LF为前体的动量矩矢量;ω1为弹轴坐标系的转动角速度矢量;MF为前体所受的合外力矩矢量;MV为后体作用于前体的滚转约束力矩矢量;FV为后体作用在前体上的约束力矢量;xF为前体质心到前、后体轴承耦合点的力臂矢量。

设动量矩LF在弹轴坐标系的投影分量分别为LF,ξ,LF,η,LF,ζ;角速度ω1在弹轴坐标系的投影分量分别为ω1ξ,ω1η,ω1ζ;外力矩MF在弹轴坐标系的投影分量分别为MF,ξ,MF,η,MF,ζ;滚转约束力矩MV在弹轴坐标系上的分量分别为MV,0,0,则矢量方程(4)在弹轴坐标系中的标量形式为

前体动量矩在弹轴坐标系中可表示为

式中:ωF,ξ,ωF,η,ωF,ζ是前体绕全弹质心转动的总角速度ωF在弹轴坐标系中的分量;由于前、后体差动自旋,近似认为ωF,η≈ωη和ωF,ζ≈ωζ,ωη,ωζ分别为全弹角速度在弹轴坐标系o′η轴和o′ζ轴上的分量。

利用式(3)～式(6),采用类似方法处理双旋弹的后体,可得绕全弹质心动力学方程:

式中:

双旋弹的绕心运动学方程为

式中:φa,φ2分别为弹体高低摆动角和方位摆动角。

以上质心运动方程和绕质心运动方程就构成了鸭式布局双旋弹的七自由度飞行动力学模型。

2.4 作用在弹上的力和力矩

在前体坐标系ox1y1Fz1F中建立鸭舵控制力模型,并将其投影到速度坐标系,可得:

式中:Fc,x1,Fc,y1分别为舵面偏转所产生的轴向力和法向力;δ1,δ2分别为弹体的高低攻角和侧向攻角;Fc,x2,Fc,y2,Fc,z2分别为鸭舵控制力在速度坐标系中的分量。

鸭舵控制力矩在弹轴坐标系中表示为

式中:ltG为舵面压心到弹体质心的距离。

舵面滚转阻尼力矩为

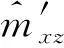
为便于研究,本文暂不考虑一些气动力和力矩的耦合效应,将作用在弹上的重力、阻力、升力、马格努斯力及翻转力矩、赤道阻尼力矩均按全弹组合体进行计算,而作用在前、后体上的马格努斯力矩和极阻尼力矩由于具有较大差别而应分别计算。

滚转约束力矩MV主要是由前、后体之间连接轴承产生的黏性阻尼力矩与滚动摩擦力矩组成。为便于分析,这里将滚动摩擦力矩折算到黏性阻尼力矩中,则有

式中:cV为折算了滚动摩擦影响的阻尼系数。

3 弹道仿真

3.1 主要仿真条件

根据以上飞行动力学模型可编制程序进行弹道仿真,主要仿真条件为:①前、后体及组合体在不同马赫数下的气动力系数采用工程方法[14]估算;②前体两对鸭舵正交布置,其中一对为减旋舵,另一对的舵偏角δc=5°,并在低速滚转下继电式偏转,单片舵面的面积为3.42 cm2;③前、后体转动惯量为Jy,F=0.011 8 kg·m2,Jx,F=0.001 2 kg·m2,Jy,A=0.042 4 kg·m2,Jx,A=0.004 3 kg·m2;④仿真时取初速v0=980 m/s,射角θ0=45°。

3.2 无控飞行弹道特性

根据以上条件首先进行无控弹道特性仿真,结果如图3～图5所示。其中,图3为舵面全程不张开和在t=30 s处张开所对应的前、后体转速变化曲线;图4和图5分别为舵面全程不张开与舵面在炮口立即张开所对应的全弹道攻角δ和偏流z曲线。

由图3可知,当舵面未张开时,出炮口后前、后体转速就产生逐渐增大的差异,前体转速衰减明显快于后体,一段时间后(图中约为10 s)前体转速基本保持为后体转速的60%左右。这主要是由于前、后体转动惯量不同导致旋转加速度不同,并形成转速差,这使两体间产生滚转约束力矩并引起两体极阻尼力矩和马格努斯力矩的差别;这些因素又反作用于转速,使弹体在舵面未张开时就形成双旋。当舵面张开后,前体转速急剧衰减,当t=60 s时,前体转速约为10 r/s,而后体转速约为196 r/s。从图中还可以看出,舵面张开与否对前体转速影响极大(差异超过100 r/s),而对后体转速变化影响较小(仅为5 r/s左右),这也是双旋弹保持飞行稳定的关键所在。

图3 不同条件下前、后体转速变化

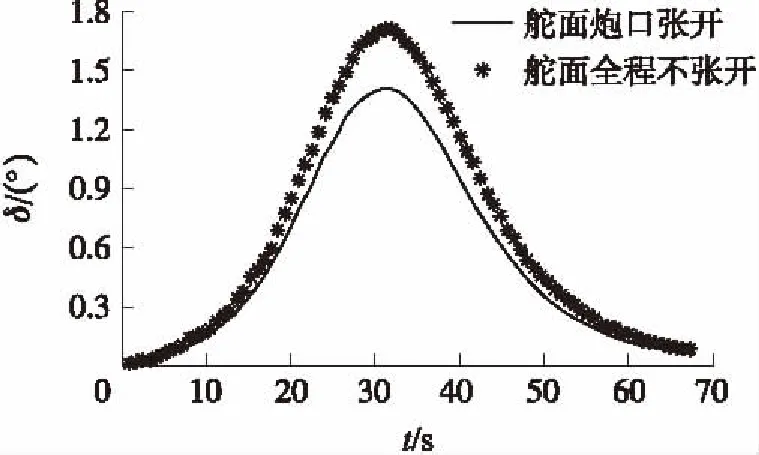
图4 不同条件下全弹道攻角δ变化

图5 不同条件下全弹道偏流z变化

根据图4、图5,与舵面全程不张开的情形相比,当舵面在炮口张开,全弹道攻角略小(图中最大差异约为0.3°),偏流也较小(图中最大差异约为100 m)。从表面上看,舵面张开时,由于鸭舵位于前部,会因弹丸攻角的存在形成一个附加翻转力矩,从而增大全弹攻角。但由于前体转速在舵面滚转阻尼作用下快速衰减并带动后体转速加速衰减,使得全弹转速明显小于舵面不张开时的转速,加之稳定飞行的弹丸攻角较小,则转速衰减的影响超过了舵面翻转力矩的影响,从而使得弹道上的动力平衡角在舵面张开条件下是减小的,进而导致偏流也减小,这符合一般的外弹道规律。从数值上看,由于前、后体参数设置较为合理,这种影响不是很大,弹丸仍可保持良好的飞行稳定性。

3.3 有控飞行弹道特性

下面考察双旋弹体在控制作用下的攻角运动响应。取鸭舵启控时刻为t=60.1 s,仿真结果如图6和图7所示。图6中的δc为舵偏角,图7中的XR表示弹丸的剩余飞行斜距离。

图6 不同舵偏角对应的攻角摆动曲线

图7 控制作用下弹轴绕速度轴的变化

图6反映了不同舵面偏转角对应的弹体攻角响应。由图所示,在鸭舵控制力和控制力矩作用下,攻角形成振荡,幅值衰减较缓慢,振荡频率逐渐加快,舵面偏转角相差2°,对应的攻角幅值也大约相差2°,舵面偏转角对弹体稳定性的影响较大。

分析图7,正的攻角分量δ2在控制力矩作用下进一步增大,但由于后体的高速自旋形成陀螺力矩,抑制了攻角的发散。在控制力矩和陀螺力矩的共同作用下,弹轴围绕速度轴形成几乎等幅的圆运动,攻角二分量δ1,δ2均是按照一定频率的弱收敛性振荡,且当控制方位γF=90°时为侧向弹道控制,δ1最大幅值小于δ2最大幅值。由于图中的攻角最大幅值并未超过一定限值(如15°),此时弹体为全弹道飞行稳定。

综上,如果控制参数或弹道参数设计不当,有可能在舵控瞬时使攻角超过最大限值,从而引起飞行失稳。而近乎等幅的攻角振荡也势必给该类有控弹的飞行控制带来负面影响,须采取一定方法对控制系统进行适配性设计,或通过对双旋弹结构、气动参数等的优化,尽可能减弱攻角振荡。

4 结束语

本文分析了鸭式布局双旋弹的飞行原理,在我国外弹道理论体系下建立了鸭舵控制双旋弹的飞行动力学模型,编制了计算程序,对其弹道特性进行了仿真分析,得到了该类旋转弹无控飞行和有控飞行时主要弹道参数的变化规律,为鸭式布局双旋弹的弹道参数优化、稳定性分析及控制方案设计等提供了理论依据。目前,国内对双旋弹的研究尚处于初步阶段,实际飞行中弹体双旋与鸭舵控制的耦合效应及其对飞行控制的影响,还需进一步的理论探讨,并结合相关试验开展深入研究。

[1] STOCKENSTROM A.A simplified approach to range dispersion reduction[C]// The 20th International Symposium on Ballistics.Orlando,USA:IBC,2002:179-185.

[2] PETTERSSON T,BURETTA R,COOK D.Aerodynamics and flight stability for a course corrected artillery round[C]// The 23rd International Symposium on Ballistics.Tarragona,Spain:IBC,2007:647-653.

[3] CORRIVEAU D,BERNER C,FLECK V.Trajectory correction using impulse thrusters for conventional artillery projectiles[C]// The 23rd International Symposium on Ballistics.Tarragona,Spain:IBC,2007:639-645.

[4] WIDMAYER R S.Terminal trajectory correction capability for standard spinning projectiles[C]// The 2nd International Symposium on Ballistics.Daytona,USA:IBC,1976:1-14.

[5] COSTELLO M,PETERSON A.Linear theory of a dual-spin projectile in atmospheric flight[J].Journal of Guidance,Control and Dynamics,2000,23(5):789-797.

[6] WERNERT P,LEOPOLD F,BIDINO D,et al.Wind tunnel tests and open-loop trajectory simulations for a 155 mm canards guided spin stabilized projectile[C]// AIAA Atmospheric Flight Mechanics Conference and Exhibit.Honolulu,Hawaii,USA:AIAA,2008:1-17.

[7] WERNERT P.Stability analysis for canard guided dual-spin stabilized projectiles[C]//AIAA Atmospheric Flight Mechanics Conference.Chicago,Illinois,USA:AIAA,2009:1-24.

[8] THEODOULIS S,WERNERT P.Flight control for a class of 155 mm spin-stabilized projectiles with course correction fuse(CCF)[C]// AIAA Guidance,Navigation and Control Conference.Portland,Oregon,USA:AIAA,2011:1-10.

[9] 揭涛,施坤林.旋转稳定弹弹道修正引信减旋装置研究[J].探测与控制学报,2007,29(5):9-12.

JIE Tao,SHI Kun-lin.Study on despining device of course correction fuze for spin-stabilized projectile[J].Journal of Detection & Control,2007,29(5):9-12.(in Chinese)

[10] 李虎全,李世义,罗会甫,等.旋转弹弹道修正引信修正能力仿真研究[J].系统仿真学报,2009,21(9):2 543-2 545.

LI Hu-quan,LI Shi-yi,LUO Hui-pu,et al.Study on correcting ability of trajectory correction fuze for spin stabilized projectiles[J].Journal of System Simulation,2009,21(9):2 543-2 545.(in Chinese)

[11] JI X,WANG H,ZENG S,et al.Lateral-directional aerodynamics of a canard guided spin stabilized projectile at supersonic velocity[J].Applied Mechanics and Materials,2012(110/116):4 343-4 350.

[12] JI X,WANG H,ZENG S,et al.Longitudinal aerodynamics of a canard guided spin stabilized projectile[J].Advanced Materials Research,2012(443/444):719-723.

[13] 韩子鹏.弹箭外弹道学[M].北京:北京理工大学出版社,2008.

HAN Zi-peng.Exterior ballistics for projectiles[M].Beijing:Beijing Institute of Technology Press,2008.(in Chinese)

[14] MOORE F G.Approximate methods for weapon aerodynamics[M].Reston,Virginia,USA:American Institute of Aeronautics and Astronautics,Inc.,2002.