陀螺外框摆动角受限时某末制导炮弹的弹道特性
2014-08-28佟德飞宋卫东刘炳辰
佟德飞,宋卫东,刘炳辰
(1.军械工程学院 火炮工程系,石家庄 050003;2.66294部队 北京 100042)
在惯性飞行阶段,末制导炮弹通过调整舵片的偏转来实现以基本不变的弹道倾角飞行,从而延长飞行距离[1]。该型末制导炮弹惯导陀螺仪为框架陀螺仪,陀螺转子沿着弹体纵轴安装。由于弹体的旋转,陀螺内框轴和外框轴随弹体一起旋转以保证转子的空间定轴特性,弹体每旋转一周,陀螺内框以及外框相对弹体交替摆动一次。外框轴摆动信号经处理实现控制信号输出并对鸭舵实施控制,实现飞行过程中对重力的补偿,即为惯导滑行增程的基本原理。
文献[2]通过仿真实验分析了基于惯导滑翔增程技术的炮弹弹道特性,不考虑陀螺结构因素影响,内、外框架的摆动不受角度限制,实际上受结构影响,内、外框摆动角度上限为48°。因此,本文分析当外框摆动幅度超过该限定值后转子定轴性发生的变化,并分析由此改变的飞行控制过程对末制导炮弹弹道特性的影响。
1 惯导陀螺系统的空间运动
1.1 内、外框架摆动运动规律
内、外框架偏转角度的计算方法仍通过几何关系的转换求解,求解关系式为[3]
L(θg,ψg)=L(γg)L(γ)L(φ,ψ)LT(γgd,θgd,ψgd)
(1)
式中:θg,ψg分别为外框、内框摆动角;γg为惯导陀螺相对弹体的安装角;γ,φ,ψ为末制导炮弹弹体姿态角;γgd为陀螺内框架相对惯性坐标系的偏转角;θgd,ψgd分别为陀螺转子相对惯性坐标系在铅垂面上及水平面上的偏转角。根据惯导陀螺结构特点,给定|θg|>48°为转子内、外框架的碰撞条件。
1.2 转子进动计算模型
目前,转子碰撞相关问题的研究对象多为汽轮机转子等大型机械,主要分析转子与周围机械部件存在摩擦碰撞情况下的动力学行为[4-6]。对于惯导陀螺仪摆角受限,外框的碰撞问题很少有文献提及。
根据转子欧拉运动方程,转子受到外力矩后的运动方程为

式中:ω1为受冲击力矩作用之前转子的转动角速度,并假设其保持恒定值。因此转子转过的角度可表示为
dr=ωxdt
(4)
将式(2)中后2个公式化为容易积分的线性方程式,将角速度化为以r为变量,即
因此可得:
将my,mz同样转换为以r为变量,引入复数量:
ωy+iωz=ω,my+imz=m
(7)
将方程(6)化为下列形式:
ω′+ipω=m
(8)
因此,式(8)的解形式为
(9)
由此,作用在转子上的力矩不同就会使其产生不同的运动。
2 转子进动分析
由于无法通过实验确定转子的外框架受限后转子的运动,本文从理论上对转子可能产生的运动分为3种情况进行研究:
①外框架摆角超限后起到限位作用。转子完全失去绕外框转动的自由度,转子随弹体进动,进动角速度方向同弹体转动角速度方向。
②外框架摆角超限后,内、外框架发生不完全弹性碰撞。通过给定碰撞冲量,分析转子受到恒定外力矩作用下的进动运动。
③外框架摆角超限后,内、外框架完全弹性碰撞,转子受到冲击力矩的作用。
2.1 限位条件下的转子进动
限位作用使陀螺系统失去一个自由度,陀螺仪变成二自由度陀螺。当弹体绕陀螺仪缺少自由度的方向转动时,将强迫陀螺仪随弹体一同转动,转子轴转动趋向与弹体转动角速度的方向重合。
2.2 常值激励力矩作用下的转子进动
由于转子固连于内框架,外框架受限后,激励力矩最后传递并作用于转子。
1)力矩向量垂直于转子对称轴。
当外框架超限后,常值激励力矩垂直于转子对称轴时,mx=0,ωx=ω1。转子在自转方向上的转动速度不变。式(2)可解耦,得转子在另外2个方向上的运动情况。解的形式为
以时间为变量的解为
2)任意方向的力矩向量。
式(2)解的形式为
相对上一种情况,转子运动还与激励作用的时间平方相关。
2.3 冲击作用力矩下的转子进动
首先假设框架摆动角度受限后存在连续碰撞的可能,用狄拉克函数δ(t)表示冲击碰撞力矩,即
式中:tν是第ν次冲击的时间,Mν是冲击力矩的模值。于是方程的解为

(15)
由于单位阶跃函数为

(16)
对该一阶线性方程进行求解,并再将时间作为变量得到:
将上述通解进行分解就可以得到转子在另外2个轴即y,z方向的角速度的值。当内、外框架摆动满足碰撞条件时,在弹体一个旋转周期内碰撞可能存在4种形式,分别为内框、外框超限情况下的正向碰撞和逆向碰撞。因此,本文给定判定方案如表1所示。

表1 碰撞正向、逆向判定
转子受到连续冲击力矩的作用后,每次冲击都会导致角速度的瞬时值发生阶跃变化,因此转子的运动为不同冲击引起转子锥形转动运动的叠加。
3 转子运动数值仿真
利用末制导炮弹弹道模型以及惯导控制模型[2],建立弹道数值仿真系统,给定惯导陀螺启动时间为12.4 s。
按照转子运动的第①种情况,当转子外框摆动角超限后起到限位作用,将三自由度惯导陀螺强制变为二自由度陀螺,转子随弹体向下进动,并在下一次外框摆角受限之前保持该偏转角度不变。在弹道降弧段,弹体向下偏转角速度约为1.5(°)/s。转子在空间中的角度变化如图1所示。
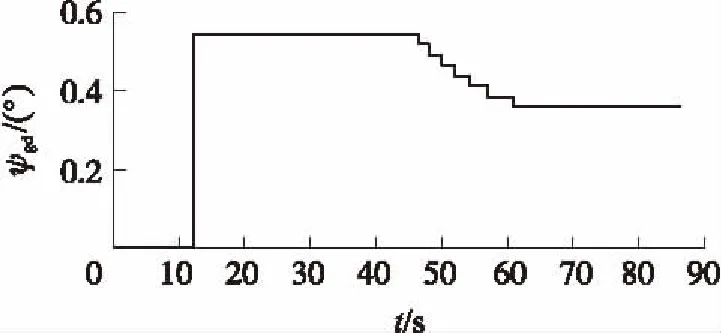
图1 限位条件下的转子偏转角度
按照限位条件进行计算时,转子在纵向平面内向下偏转,随载体向下进动,进动约0.183 rad。按照转子运动的第②种情况,转子将同时绕内、外框轴偏转;如图2所示。
按照恒值力矩条件进行计算时,转子在水平面以及纵向平面偏转相同的角度,但变化过程比较平缓,转子分别转过-0.19 rad。恒值力矩激励作用下的转子运动是锥形运动。按照转子运动的第③种情况,转子转动角速度受到冲击激励力矩作用的影响。给定外框架碰撞时刻相互作用力矩,并在0.005 N·m~0.02 N·m之间取值。转子空间偏转角速度变化情况如图3所示。

图2 恒值力矩条件下转子偏转角度
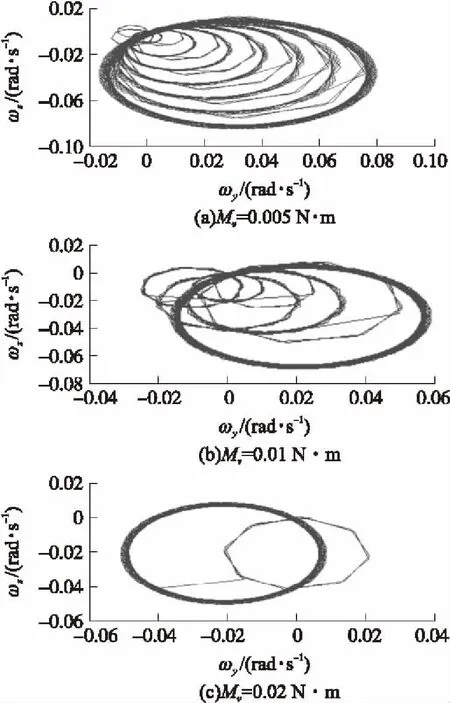
图3 不同冲击力矩时的转子摆动角速度
转子受到力矩作用后在空间发生锥形运动,每次碰撞都使转子偏转半径或角度不断增大。对上述转子空间偏转角速度进行积分,就得到转子偏离原转动轴的偏转角度。积分结果如图4所示。
按照冲击力矩激励条件进行计算时,转子在空间摆动运动复杂,由于转子的空间运动由锥形运动进行叠加,对其进行积分就得到转子在空间的偏转情况。当给定冲击力矩为0.02 N·m时,转子向下以及向右偏转-0.77 rad;当给定冲击力矩为0.01 N·m时,转子向下以及向左偏转分别约为-1.3 rad,0.65 rad;当给定冲击力矩为0.005 N·m时,转子向下以及向左偏转分别约为-1.2 rad,1.1 rad。

图4 冲击力矩条件下转子空间偏转角度
转子定向性的变化对末制导炮弹的弹道特性产生了很大的影响。
4 外框摆动角超限对弹道特性的影响
根据末制导炮弹弹道方程,对末制导炮弹弹道特性进行数值仿真。当外框摆动角超过限制后,转子空间定轴性受限受到影响,进而对控制过程的计算基准产生计算误差。
外框摆动角不受限制条件下,图5(a)为整个飞行过程中外框架摆动角的变化规律,图5(b)为图5(a)局部视图。

图5 不受限条件下外框摆动规律及局部摆动视图
考虑实际情况,当转子外框受到限制时,按限位条件计算,转子失去一个自由度,于是转子轴随载体进动。由于每次改变转子角度并不大,转子轴与弹轴夹角的减小并不能保证在第一次外框摆角超限后不再超过该限制。限位条件下,飞行过程中的外框摆动角如图6所示。

图6 限位条件下外框摆动规律
转子受到恒值力矩条件下,每次转子偏转角度较小,外框架摆动规律如图7所示。
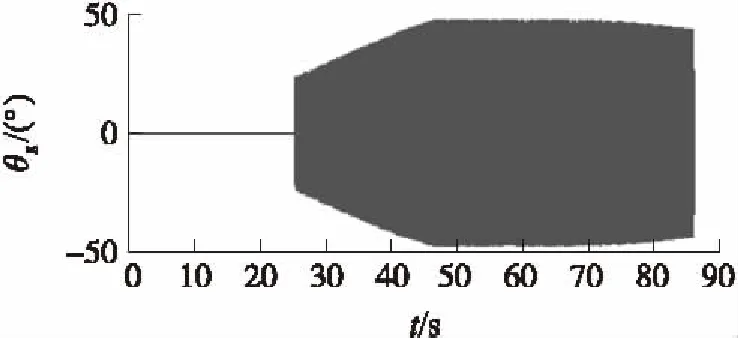
图7 恒值力矩条件下外框摆动规律
图8为外框摆动角受限后转子受到不同冲击力矩条件下外框架的摆动规律。3种工况都使转子轴与弹轴夹角不断减小。

图8 不同冲击力矩条件下外框摆动规律
根据数值计算,外框摆动过程按照不同计算方式差异比较明显,并且造成的弹道特性差距也很大,具体给定的数值如表2所示。

表2 不同结构条件下名义弹道落点诸元
不受结构限制条件下,通过仿真计算,外框摆动角也超过-55°~55°的摆角测量范围,因此对控制信号作不输出处理。因此,落角增大,并且未保持在惯导滑行阶段以-26°左右倾角飞行,这证明惯导滑行阶段控制舵片偏转并未起到重力补偿的作用。
从表中可以看出,按照限位条件以及恒值力矩条件计算时,转子空间角度的变化并不剧烈,同时在控制弹体惯性滑行阶段,能够保证其弹道倾角缓慢变化,减小飞行落角。飞行距离较不受限条件分别增加约2 228 m,2 058 m,侧偏变化约-41.9 m,570.8 m。
按照冲击力矩计算时,转子空间摆动变化较大,每次结构上的限制都使转子轴与弹轴夹角减小,使其控制过程发生如图8所示的变化规律。通过给定单次碰撞所产生的冲击力矩计算得到,当冲击力矩越小时,最终落点单元的落角越大且造成的转子空间偏转角度也大。最终落角都要比-26°大得多,也说明了舵片参与重力补偿的不充分。与不受限情况进行比较时,弹道性能在射程、侧偏等因素方面差距较大。飞行距离较不受限条件分别增加约1 019 m,732 m,436 m,侧偏变化约748.3 m,-599 m,-920.2 m。
根据数据比较,可以得出结论:①当转子外框摆动角受结构限制而仅起限位作用时,转子随载体进动。由于载体偏转变化平缓,惯导控制过程能够较为准确地提供重力补偿,使弹体能够惯性滑行,延长飞行距离。②当转子外框摆动角受限后,受到冲力矩的作用而进动时,外框摆动角受限最终的结果就是转子圆锥运动的叠加。计算表明转子运动变化较为剧烈,控制过程变化未能使弹体惯性滑行段提供有效的重力补偿,飞行距离有一定的变化,但造成的侧偏很大。
5 结论
本文从理论上分析了末制导炮弹惯导陀螺外框架摆动受限后,其可能造成转子发生的3种运动。采用欧拉运动学方程建立了转子运动计算模型,分析了转子在限位条件、恒值激励力矩、不同冲击力矩作用下转子的进动运动。结合末制导炮弹外弹道模型并进行了数值仿真,分别研究了外框摆动角受限后3种转子进动模型对弹道特性造成的影响。限位条件下,转子跟随弹体运动,对弹道性能影响不大;恒值力矩激励条件下,力矩越大,对弹道影响越大;冲击力矩作用下,转子空间运动为锥形运动的叠加,对弹道性能影响很大。本文为深入分析末制导炮弹在极限运动条件下的弹道特性提供了理论基础。
[1] 宋卫东,张进忠.惯导陀螺零漂对末制导炮弹弹道性能的影响[J].南京理工大学学报,2010,34(2):162-163.
SONG Wei-dong,ZHANG Jin-zhong.Influence of zero drift of inertial guide gyro on trajectory characteristics of terminal guide shell[J].Journal of Nanjing University of Science and Technology,2010,34(2):162-163.(in Chinese)
[2] 赵庆岚.激光末制导炮弹弹道特性及射表编拟方法研究[D].石家庄:军械工程学院,2008.
ZHAO Qing-lan.Research on ballistic performance and method of making firetable of laser terminal guidance projectile[D].Shijiazhuang:Ordnance Engineering College,2008.(in Chinese)
[3] 刘炳辰.基于多刚体理论的某型末制导炮弹弹道建模与仿真[D].石家庄:军械工程学院,2011.
LIU Bing-chen.Modeling and simulation of terminal guide projectile trajectory based on multi-body dynamics theory[D].Shijiazhuang:Ordnance Engineering College,2011.(in Chinese)
[4] 孙政策,徐建学,周桐.高速碰摩转子的复杂动力学行为分析[J].机械科学与技术,2002,12(6):923-928.
SUN Zheng-ce,XU Jian-xue,ZHOU Tong.Analysis of the complicated characteristics of a high-speed rotor system with rub-impact[J].Mechanical Science and Technology,2002,12(6):923-928.(in Chinese)
[5] 王秉仁,刘兆阳.基于非线性理论的碰摩转子动力学特性研究[J].汽轮机技术,2006,48(6):422-426.
WANG Bing-ren,LIU Zhao-yang.Research on dynamic character of rub-impact based on nonlinear theory [J].Turbine Technology,2006,48(6):422-426.(in Chinese)
[6] 王涛,傅行军.基于Hertz接触模型的碰摩转子动力学响应研究[J].汽轮机技术,2009,51(1):39-42.
WANG Tao,FU Xing-jun.Dynamic response of rub-impact rotor based on Hertz contact model [J].Turbine Technology,2009,51(1):39-42.(in Chinese)
[7] 佟德飞,宋卫东,贾波.陀螺转子质量偏心对末制导炮弹弹道特性的影响[J].弹道学报,2014,26(1):26-31.
TONG De-fei,SONG Wei-dong,Jia Bo.Influence of gyroscope rotor mass eccentricity on ballistic of terminal guided projectile[J].Journal of Ballistic,2014,26(1):26-31.(in Chinese)
