基于改进人工鱼群算法的无人艇控制参数优化

廖煜雷，刘鹏，王建，张铭钧，2

(1.哈尔滨工程大学 水下机器人技术重点实验室，黑龙江哈尔滨150001;2.哈尔滨工程大学 机电工程学院，黑龙江 哈尔滨150001)

近年来，随着海洋资源勘探与开发、海洋安全越来越受到人们的高度重视，无人艇(unmanned surface vehicle，USV)由于在海洋科研、海洋安全等方面具有广泛的应用潜力，逐渐成为了国际研究热点［1-2］。一些学者针对欠驱动USV的控制问题进行了深入探讨［3-6］，欠驱动USV控制系统的参数优化存在分析复杂、多参数、强非线性等难点，是典型的非线性系统最优控制问题。在该类系统的设计中，一般依据设计者的经验，采用试凑的方法来调整控制参数，这样难以得到最优、甚至次优的控制参数。一种可能的解决办法是利用优化算法进行参数寻优，目前常用的优化方法有模拟退火、遗传、蚁群、粒子群、人工鱼群等算法。文中针对控制参数调节困难的问题，考虑将人工鱼群算法(artificial fish swarm algorithm，AFSA)应用到USV控制系统的参数优化中，为解决非线性控制参数的优化问题提供一种有效途径。由于AFSA具有对参数、初值和目标函数等要求低，分布并行寻优、全局收敛性好、收敛迅速等诸多优点［8］，在控制参数优化［8］、股票预测［9］、模型辨识［10］、数据挖掘［11］、通信网络优化等领域均有应用。然而AFSA也存在求解精度低、后期收敛缓慢、算法退化等问题［12-15］。

本文针对AFSA存在的收敛缓慢等问题，考虑引入生存机制、寻优过程评估、动态调整参数等方法，提出了一种改进人工鱼群算法(improved artificial fish swarm algorithm，IAFSA)，并利用IAFSA解决欠驱动USV的控制参数优化问题。

1 控制系统设计

1.1 控制问题描述

本文讨论的一类欠驱动USV的水平面运动模型如图1。该USV仅有的控制输入为纵向推力F和转艏力矩T(2个控制输入)，少于系统输出维数(3自由度)，因此该USV具有欠驱动性。

图1 无人艇的水平面运动模型Fig.1 USV model in plane motion

在一定假设条件USV的运动和动力学模型可描述为［16］

式中:x、y表示船的重心在惯性坐标系{I}中的位置，ψ是船的艏向角;u、υ、r分别表示在船体坐标系{B}中船的纵向、横向和偏航(角)速度;τ1、τ2、τ3分别表示船在纵向、横向、艏向受到的有界环境干扰力;参数mii和dii分别是船的惯性和阻尼参数矩阵在{B}系3个坐标轴上的分量，模型参数存在有界不确定性。

选用文献［17］中的轨迹规划方法，假设在惯性系{I}中USV重心G所跟踪的轨迹是惯性系下位置变量xd(t)、yd(t)关于时间的函数，下标“d”表示期望变量。、为惯性系{I}下的参考速度:

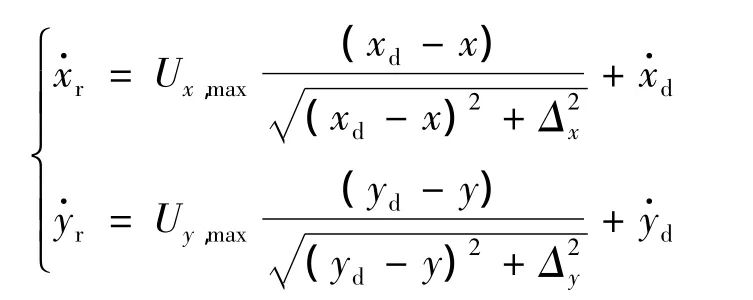
式中:下标“r”表示参考变量;正常数Ux，max、Uy，max表示USV向期望轨迹运动的最大接近速度，其大小由USV的机动能力决定;Δx、Δy为调节因子，用于调节跟踪过程的动态行为。通过坐标变换，船体坐标系{B}下的参考跟踪速度ur、υr和加速度可表示为

因此USV的轨迹跟踪控制目标为:设计反馈控制律保证USV跟踪上参考速度，并最终收敛到期望轨迹。

1.2 控制器设计

下面基于滑模控制理论［16-18］，分别设计纵向和横向的轨迹跟踪控制器［16］。

1.2.1 纵向控制器设计

纵向滑模表面采用一阶的指数镇定面:

式中:ue=u-ur表示纵向速度差。

设计纵向滑模控制器为

式(1)中模型参数和干扰力的不确定界限为

定义Lyapunov函数:将V1对时间求导，并将式(1)、(2)代入，可得

选择k1为

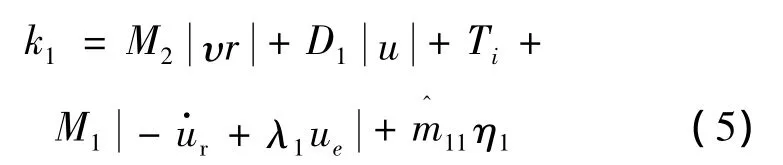
式中:η1为正常数。

将式(5)代入式(4)可知，V1满足可达条件:

1.2.2 横向控制器设计

横向滑模表面定义为二阶的指数镇定面:

式中:υe=υ-υr表示横向速度差。

将S2对时间求导，并设其导数为零，可得等式:

将式(1)、(7)代入式(6)，可得名义横向控制器

式中:h、b的表达式为

设计横向滑模控制器为

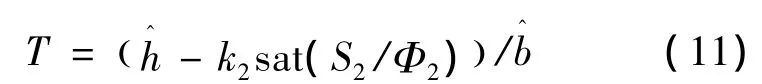
式中:Φ2为边界层厚度。定义Lyapunov函数:

将V2对时间求导，并把式(6)～(11)代入，可得

选择k2为

式中:η2为正常数;H为h的不确定性范围，且满足;β的范围依赖于b的几何平均数，详细定义见文献［18］。

将式(13)代入式(12)可知，V2满足可达条件

根据文献［16］的分析过程可证明，控制器式(3)、(11)保证了轨迹跟踪系统的渐近稳定性，且艏摇运动r是有界输入-有界输出稳定的。

2 改进人工鱼群算法

2.1 人工鱼群算法

李晓磊［8］提出了人工鱼群算法。该算法基于动物自治体的概念，通过模拟自然界中鱼群的觅食、追尾、聚群等行为，并模拟鱼群集体协作的社会行为，以最终实现集群智能的一种仿生型群智能优化算法。

AFSA中基本概念与参数的定义:为最大目标搜索空间的维度;表示欲寻优变量的求解域，即表示人工鱼的视野;为人工鱼的最大移动步长;κ为拥挤度系数;为试探次数;n为人工鱼群体的总数量;X表示人工鱼群整体，X=[X1，X2，…，Xn]T;第i条人工鱼的状态表示为向量Xi=(xi1，xi2，…，)，(i=1，2，…，n);人工鱼个体间的距离为;人工鱼当前所在位置的食物浓度为Yi=f(Xi)，即Y为目标函数值为最大迭代次数，表示第次迭代。文中以求取极大值为例进行讨论。

大量文献研究表明［11-15］，虽然AFSA具有很多突出优点，但也存在一些问题:1)在搜索前期收敛速度快，但后期收敛变慢;同时搜索缺乏协调性，易出现“算法退化”现象。2)对最优精确解的获取能力不够，仅能得到全局最优解的邻域。3)鱼群群体缺乏协调性和交互性。公告板是自下而上的交互(个体行为可以影响到群体最优解)，而没有自上而下的交互(群体最优解没有对个体行为施加影响)。

2.2 改进人工鱼群算法

在AFSA提出后，很多研究者曾尝试改进其算法，主要改进思路:1)对算法本身提出了很多的改进措施，例如:弹性自适应AFSA、极坐标编码AFSA、生境式AFSA、分解协调式AFSA等;2)将不同的优化算法相结合或融合，通过利用各自算法的长处以实现优势互补，例如:AFSA与蚁群、AFSA和模拟退火、AFSA同 Hopfield网络、AFSA与遗传算法等。

文中提出一种改进人工鱼群算法(IAFSA)，主要改进思想:引入生存机制以提高群体的进化能力和协调性;随着寻优的进行，自适应地调整鱼群参数和求解域，并最终实现全局性、自适应、高速、高精度的寻优目标。下面讨论几点改进方法。

2.2.1 搜索过程的评估和行动策略的调整

将寻优过程动态地分为3个阶段，前期、中期、后期。前期:对整个求解域进行粗略搜索，确定局部最优求解域。中期:淘汰部分局部最优解域，定位全局最优求解域。后期:重点在最优解域附近开展精细搜索，提高求解精度。对于求解极大值问题，采用的评估方法为

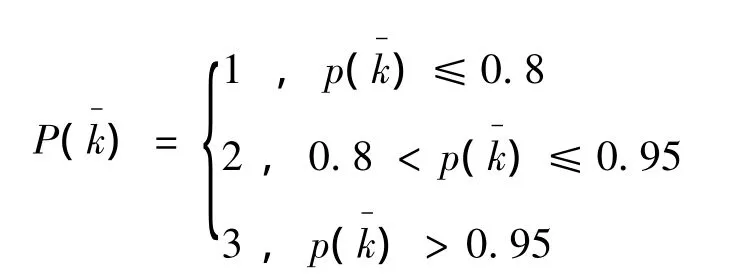
其中:

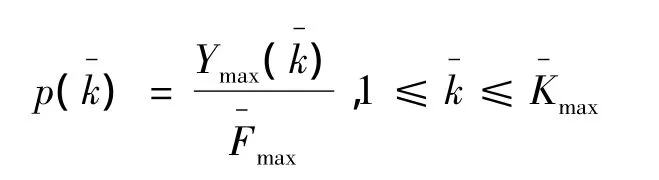
行动策略选为:前期和中期采用进步最快策略，预先开展3种行为，而后选择最优者执行，若3种行为仍未进步则执行随机行为。而后期采用进步即可的策略，即先觅食行为，如取得进步即退出，否则执行聚群行为，这两行为均无进步则采取追尾行为，若3种行为仍未进步才采取随机行为。

2.2.2 动态调整鱼群参数

鱼群参数对算法性能有直接影响:视野越大，越利于搜索全局极值并收敛，反之则越利于局部搜索;步长越大，越易搜索全局最优，但同时降低了求解精度;拥挤度因子避免了过度拥挤而陷入局部最优，然而由于排斥作用而难以逼近精确解。参数调整原则:既要保证前期全局粗略搜索和快速收敛，也要兼顾后期对定位的最优解域进行精细搜索。调整方法为

式中:ρ1、ρ2、ρ3、ρ4表示调整系数，均大于1。分别为初始视野和拥挤度。

2.2.3 生存机制

在自然界中，如果某条小鱼长期处于缺乏食物状态(食物浓度较低)，该鱼往往因生命力降低而逐渐被淘汰。尤其是在搜索中、后期，当某条人工鱼仍处于低食物浓度状态时，若继续让这条鱼存活，势必会降低群体的生存能力，影响群体的进步性。

基于上述事实，文中引入生存机制——在搜索的前期，对食物浓度较低人工鱼的鱼群参数进行调整，扩大其视野、步长，使其有更大的生存机会;而在中、后期，将食物浓度较低的人工鱼淘汰，并将其引导至最优解域附近。为此定义第i条人工鱼的生存因子为

式中:ρ5为调整系数，满足ρ5＞1。

2.3 优化目标函数和算法流程

在最优控制设计中，性能指标可用Bolza代价函数表示为［19］

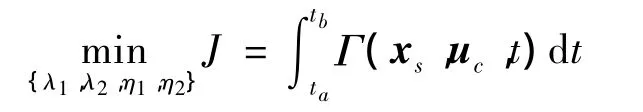
式中:xs为系统状态，uc为控制输入，且满足(xs，uc，t);λ1、λ2、η1、η2为欲寻优的控制参数。

在USV实际操控中，常选用一定的性能指标，比如最小跟踪误差、最小能量消耗等。

1)最小跟踪误差目标。

这种情况下，代价函数表示为

式中:L定义为USV重心与期望轨迹间的距离，L

2)最小能量消耗目标。

这种情况下，代价函数表示为

且满足约束条件

算法基本流程如下:

2)运行第+1次迭代，对寻优过程进行评估，并设定行动策略，然后动态地调整鱼群参数。

3)执行生存机制，若某人工鱼Xi食物浓度较低，则更新其鱼群参数或求解域。

4)按照行动策略，各人工鱼Xi执行觅食、聚群和追尾等行为。如果某人工鱼优于公告板，则用该人工鱼来更新公告板。

5)判断是否满足退出条件(最大迭代次数、满足寻优精度等条件)。本文以达到最大迭代次数为终止条件，即时算法退出，否则转到第2步，继续执行。

3 仿真结果与分析

为验证所提出优化算法的有效性，下面进行数值仿真对比试验。仿真软件环境为MATLAB 7.1，计算机CPU为Intel Core Duo主频2.33 GHz，内存为2 GB。仿真中USV考虑了推力和转艏力矩的饱和性限制，其具体参数如下:

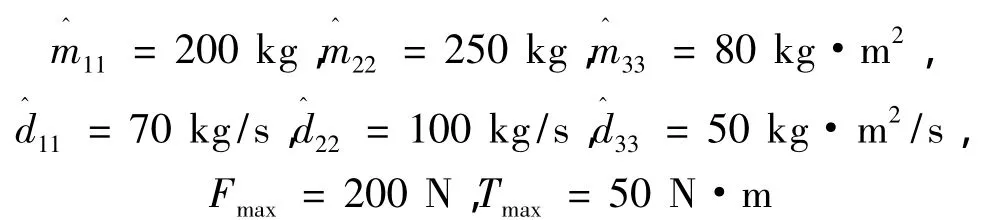
考虑到USV的机动能力，选取轨迹规划的参数为

讨论如下

圆形运动轨迹。仿真初始状态设置为:x=-4 m，y=2 m，ψ=15o，u=υ=r=0。为了对比方便，以文献［16］中参数为原始控制参数 λ1，o=0.2，λ2，o=0.5，η1，o=0.001，η2，o=0.1，Φ1=0.1，Φ2=0.1 。

鱼群参数设置:根据调试经验，选取待优化参数范围为0＜λ1，λ2≤5;0＜η1，η2≤0.5 ，则 AAFSA的鱼群参数选为

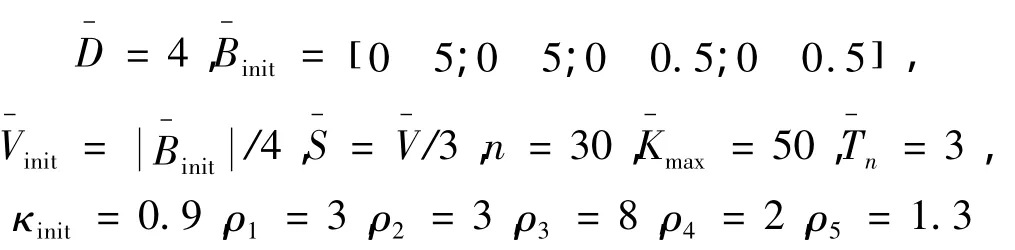
若以式(14)为目标函数(最小跟踪误差优化目标)，则可得优化后 USV 的控制参数为:λ1，T=0.95，λ2，T=0.46，η1，T=0.01，η2，T=0.07 。同理，若以式(15)为目标函数(最小能量消耗优化目标)，则可得优化后 USV 的控制参数为:λ1，E=0.7，λ2，E=0.27，η1，E=0.009，η2，E=0.056 。在上述3 组控制参数下进行仿真，仿真试验结果如图2～4所示。

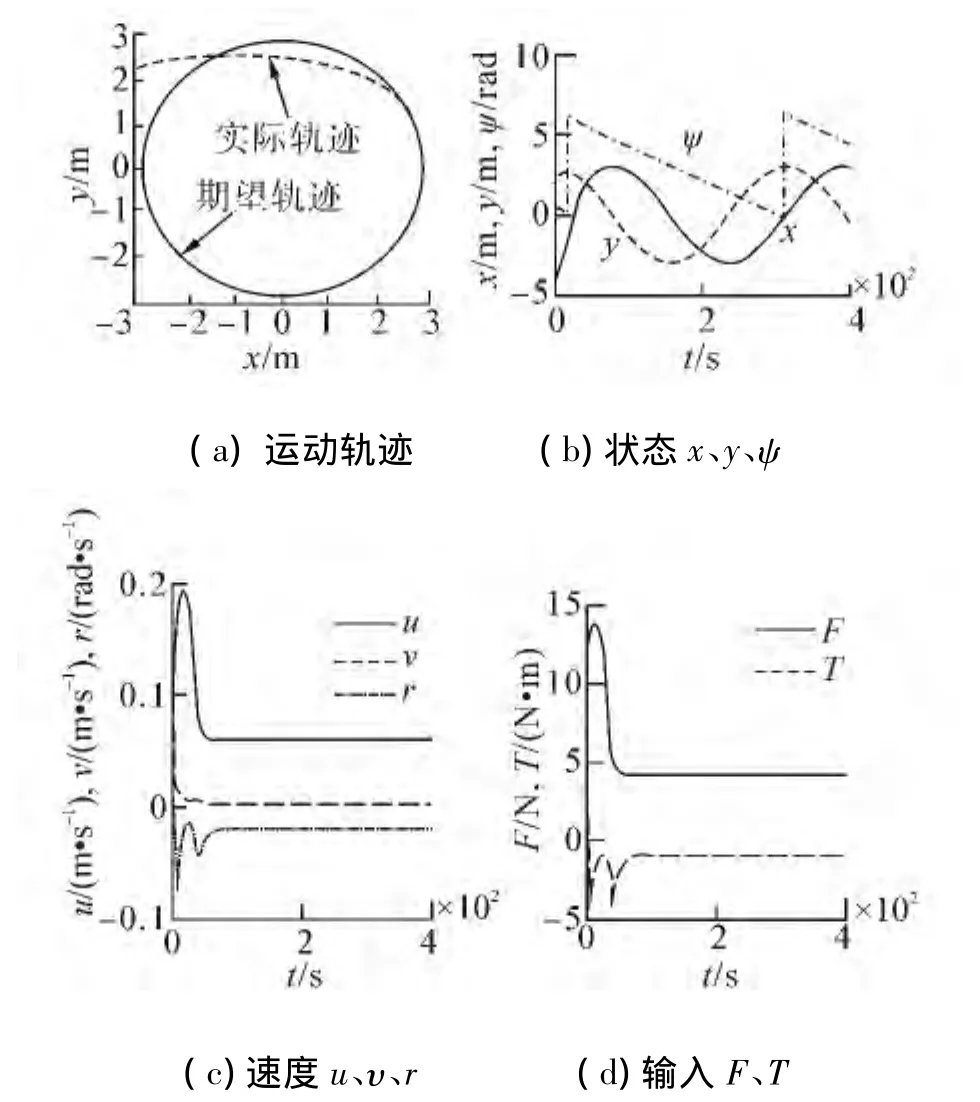
图2 原始参数下轨迹跟踪Fig.2 Response curves of USV under original parameters

图3 最小误差优化下轨迹跟踪Fig.3 Response curves of USV under minimal tracking error

从图2～4可以看出，3组参数均能驱使USV迅速地跟踪上期望轨迹，状态输出光顺、无超调，皆具有良好的动态性能。图5显示了3组参数作用下，USV的跟踪误差响应曲线。从图5可知，原始参数下的跟踪误差值为93。而最小误差优化参数下的跟踪误差值为57，减小了39%(且3组参数中，镇定时间最短);最小能量优化参数下的跟踪误差值为66，减小了29%。

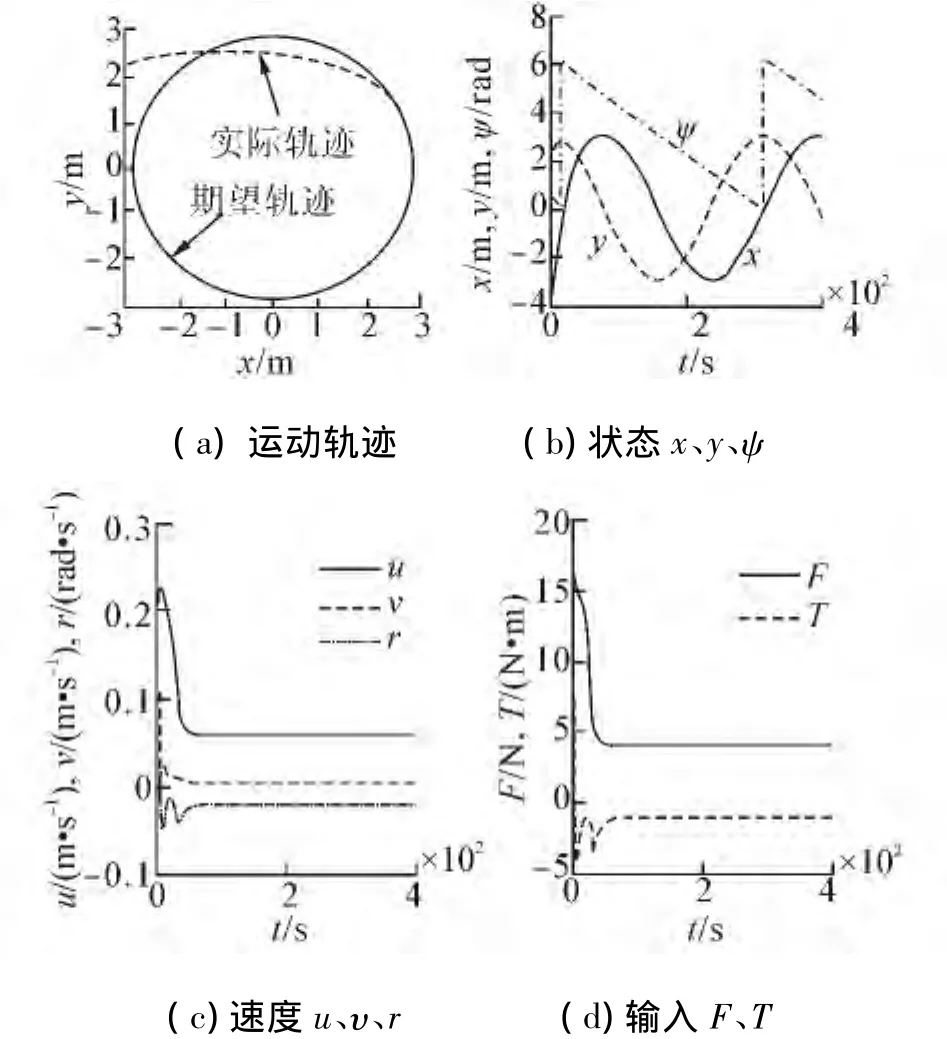
图4 最小能量优化下轨迹跟踪Fig.4 Response curves of USV under minimal energy consumption

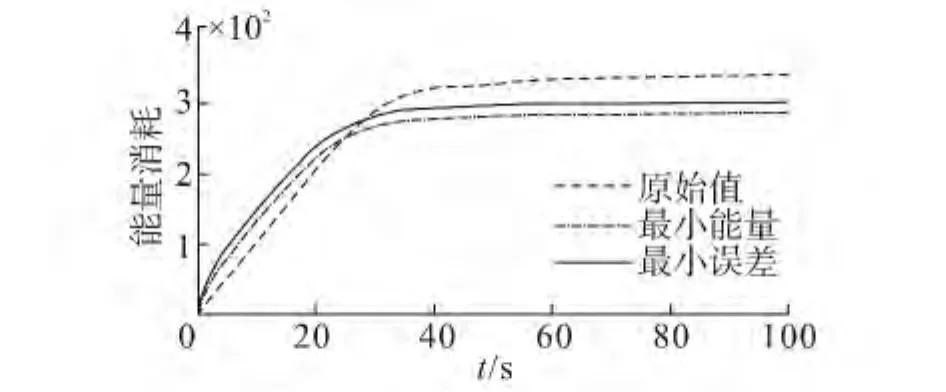
图5 跟踪误差的对比曲线Fig.5 Comparison curves of tracking error

图6显示了3组参数作用下，USV的能量消耗响应曲线。从图6可知，原始参数下的能量消耗值为351。而最小误差优化参数下的能量消耗值为308，减小了12%;最小能量优化参数下的能量消耗值为281，减小了20%，且镇定时间较短。显然，利用文中优化方法对欠驱动USV控制系统进行优化设计的控制参数，可以实现预定的优化目标，并具有良好的控制性能。

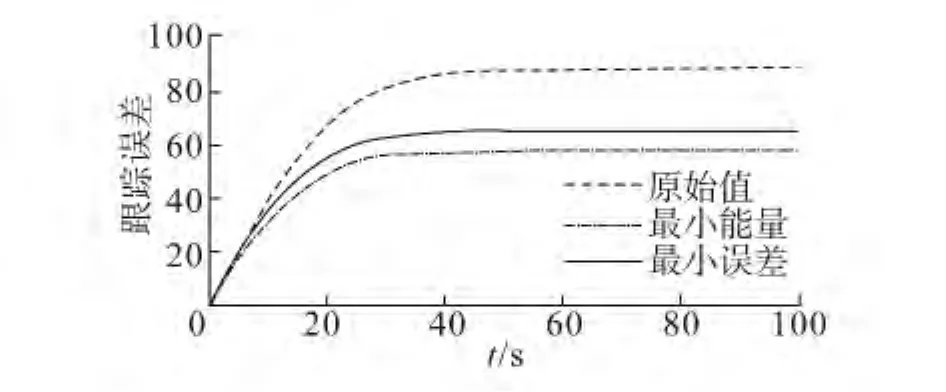
图6 能量消耗的对比曲线Fig.6 Comparison curves of energy consumption

4 结语

针对人工鱼群算法存在的问题，提出了一种改进人工鱼群算法，并成功运用该算法对欠驱动无人艇的控制参数进行了优化，得到如下结论:

1)考虑到人工鱼群算法的不足，通过引入生存机制、寻优过程评估和动态调整参数等方法，提出了一种改进人工鱼群算法。

2)利用改进人工鱼群算法，解决了欠驱动无人艇控制系统设计中的参数优化问题。仿真对比试验表明，利用该算法得到的优化参数，实现了预定优化目标，并具有良好的控制性能。

［1］VEERS J，BERTRAM V.Development of the ASV multimission surface vehicle III［C］//Proceedings of the 5th International Conference Computer and IT Application in the Maritime Industries.Leiden，Netherlands，2006:345-355.

［2］MANLEY J E.Autonomous surface vessels，15 years of development［C］//Proceedings of Oceans 2008 MTS/IEEE Quebec Conference and Exhibition.Quebec City，Canada，2008:1-4.

［3］CACCIA M，BIBULI M，BONO R，et al.Basic navigation，guidance and control of an unmanned surface vehicle［J］.Autonomous Robots，2008，25:349-365.

［4］CACCIA M，BRUZZONE G，BONO R.A Practical approach to modeling and identification of small autonomous surface craft［J］.IEEE Journal of Oceanic Engineering，2008，33(2):133-145.

［5］BIBULI M，BRUZZONE G，CACCIA M.Path-following algorithms and experiments for an unmanned surface vehicle［J］.Journal of Field Robotics，2009，26(8):669-688.

［6］LIAO Y L，WAN L，ZHUANG J Y.Full state-feedback stabilization of an underactuated unmanned surface vehicle［C］//Proceeding of the 2nd IEEE International Conference on Advanced Computer Control.Shenyang，China，2010:70-74.

［7］XU Liying，WEN Hui，ZENG Zhezhao.The algorithm of neural networks on the initial value problems in ordinary differential equations［C］//Proceedings of the 2007 Second IEEE Conference on Industrial Electronics and Applications.Harbin，China，2007:813-816.

［8］李晓磊.一种新型的智能优化方法—人工鱼群算法［D］.杭州:浙江大学，2003:1-64.LI Xiaolei.A new intelligent optimization method-artificial fish swarm algorithm［D］.Hangzhou:Zhejiang University，2003:1-64.

［9］SHEN Wei，GUO Xiaopen，WU Chao.Forecasting stock indices using radial basis function neural networks optimized by artificial fish swarm algorithm［J］.Knowledge-Based Systems，2011，24(3):378-385.

［10］师彪，李郁侠，何常胜，等.水轮机智能调速系统数学模型仿真及参数辨识［J］.电力自动化设备，2010，30(4):10-15.SHI Biao，LI Yuxia，HE Changsheng，et al.Hydraulic turbine intelligent governing system mathematical model and its parameters identification［J］.Electric Power Automation Equipment，2010，30(4):10-15.

［11］WU Huafeng，CHEN Xinqiang，SHI Chaojian，et al.An ACOA-AFSA fusion routing algorithm for underwater wireless sensor network［J］.International Journal of Distributed Sensor Networks，2012，1(1):1-9.

［12］SAEED F.Efficient job scheduling in grid computing with modified artificial fish swarm algorithm［J］.International Journal of Computer Theory and Engineering，2009，1(1):13-18.

［13］JIANG Mingyan，CHENG Yongming.Simulated annealing artificial fish swarm algorithm［C］//Proceedings of the 8th World Congress on Intelligent Control and Automation.Jinan，China，2010:1590-1593.

［14］廖煜雷.无人艇的非线性运动控制方法研究［D］.哈尔滨:哈尔滨工程大学，2012:63-69.LIAO Yulei.Nonlinear Motion control methods of unmanned surface vehicle［D］.Harbin:Harbin Engineering University，2012:63-69.

［15］廖煜雷，苏玉民，张磊.一种自适应人工鱼群算法及其在无人艇控制中的应用［J］.中南大学学报:自然科学版，2013，44(10):4109-4116.LIAO Yulei，SU Yumin，ZHANG Lei.Adaptive artificial fish swarm algorithm and application in the control of unmanned surface vessel［J］.Journal of Central South University:Science and Technology，2013，44(10):4109-4116.

［16］廖煜雷，庄佳园，李晔，等.欠驱动无人艇轨迹跟踪的滑模控制方法［J］.应用科学学报，2011，29(4):428-434.LIAO Yulei，ZHUANG Jiayuan，LI Ye，et al.Slidingmode trajectory tacking control for underactuated autonomous surface vehicle［J］.Journal of Applied Sciences，2011，29(4):428-434.

［17］廖煜雷，庞永杰.一类欠驱动机械系统轨迹跟踪的滑模控制方法［J］.中南大学学报:自然科学版，2011，42(Suppl.1):219-227.LIAO Yulei，PANG Yongjie.Sliding-mode trajectory tacking control for a class of underactuated mechanical system［J］.Journal of Central South University:Science and Technology，2011，42(Suppl.1):219-227.

［18］ASHRAFIUON H，MUSKE K R，MCNINCH L，et al.Sliding model tracking control of surface vessels［J］.IEEE Transactions on Industrial Electronics，2008，55(11):4004-4011.

［19］MCNINCH L C，ASHRAFIUON H，MUSKE K R.Optimal specification of sliding mode control parameters for unmanned surface vessel systems［C］//Proceedings of the 2009 American Control Conference.MO，USA，2009:2350-2355.