共形阵列天线超宽频带波达方向实时估计

司伟建，万良田，刘鲁涛，田作喜，蓝晓宇

(1.哈尔滨工程大学信息与通信工程学院，黑龙江哈尔滨150001;2.大连测控技术研究所水下测控技术国家重点实验室，辽宁大连116013;3.沈阳航空航天大学电子信息工程学院，辽宁沈阳110136)

共形天线已经被应用在雷达、声呐、无线通信等许多领域［1］。特别是集成在星载飞行器、航天飞行器、导弹以及陆地交通工具上。共形天线具有优越的空气动力学性能，节省空间体积，消除随机引入的视线误差，可以增加天线潜在的孔径等优点［2-3］，今后共形天线将具有很好的应用前景。

由于共形载体变化的曲率，传统的波达方向(direction of arrival，DOA)估计算法，例如 MUSIC算法和ESPRIT算法不能直接应用到共形阵列中。文献［4-5］提出了具有高分辨率的共形阵列天线DOA估计算法。文献［4］利用MUSIC算法和子阵分割技术实现共形阵列天线的DOA估计，但是谱峰搜索的计算量太大。文献［5］提出了一种基于柱面共形阵列天线的DOA和频率联合估计算法。然而文献［4-5］中导向矢量的数学模型过于复杂，并且阵元之间的间距必须为半波长［6］。当入射信号频率相对较高时，阵元之间的距离过于靠近，相邻阵元之间的互耦十分严重［7］。干涉仪测向方法是另一类波达方向估计方法，它可以用来进行超宽频带测向［8-9］。文献［8］中的方法不需要网格搜索，估计结果是闭式解，适于实时处理的情况。文献［9］总结了常用的干涉仪测向方法。然而文献［8-9］假设天线是共平面的。共形在飞行器的共形阵列天线，天线阵元很难在一个平面内，上述提到的方法都不能有效的工作。

在本文中，提出了一种基于共形阵列天线的任意基线测向方法，任意基线算法结合虚拟基线方法进行角度估计。相比MUSIC类算法，本文算法的计算复杂度更低，各个阵元之间的距离可以远大于半波长;相比其他的干涉仪测向算法，理论上天线可以被安排在空间任意位置。

1 共形天线的应用

文献［1］指出对数周期天线(log-periodic dipole antenna，LDPA)可以作为共形在载体表面的共形天线。LDPA具有很宽的带宽，它的增益比普通的平面螺旋天线高。LDPA是一种独立的频率不变超宽频带天线。一般来说，它的电特性可以在10∶1的带宽或者更高范围内保持不变。此外，天线的安装也大为简化，不会破坏载体的机械结构。图1给出了LDPA的结构示意图。它包含N个并行线性振子，它的定义为

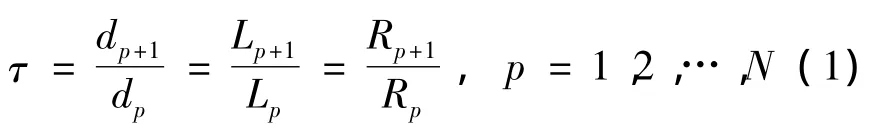
式中:dp是第p个与第p+1个振子之间的距离，Lp是第p个单元振子的长度，Rp是第p个振子到天线虚拟顶点的距离，LDPA的整体结构取决于收缩因子τ和结构角度η。

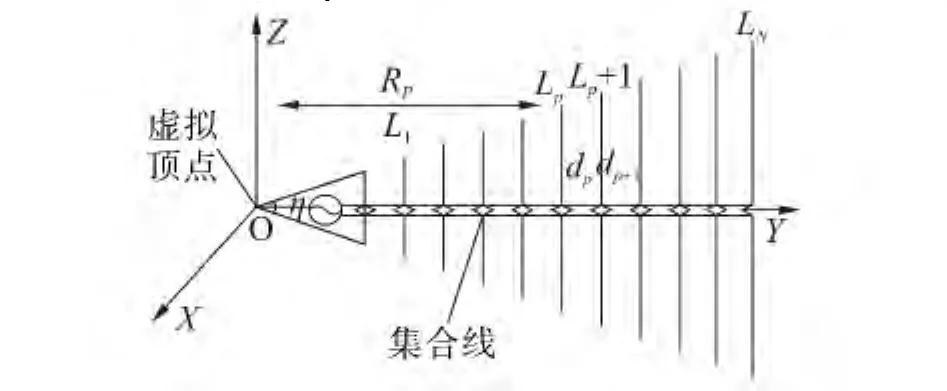
图1 LDPA结构示意图Fig.1 The structure diagram of LPDA

而LDPA没有真正的相位中心，但是存在虚拟相位中心，它位于活动区域，随着频率的改变沿着集合线移动。入射信号的频率可以用数字接收机进行测量。一旦天线在载体的安装位置确定后，可以用HFSS仿真软件确定或者在微波暗室中进行实际测试，得到不同频率的虚拟相位中心的位置(频率的步长依赖于精度需要)。频率和对应的虚拟相位中心位置存储在数据管理中心内，虽然数据量很大，但是它可以作为一个预处理过程进行“离线”处理。

2 任意基线算法测向原理

任意基线模型如图2。A、B、C是空间的3个天线阵元。α和β分别代表入射信号的方位角和俯仰角。

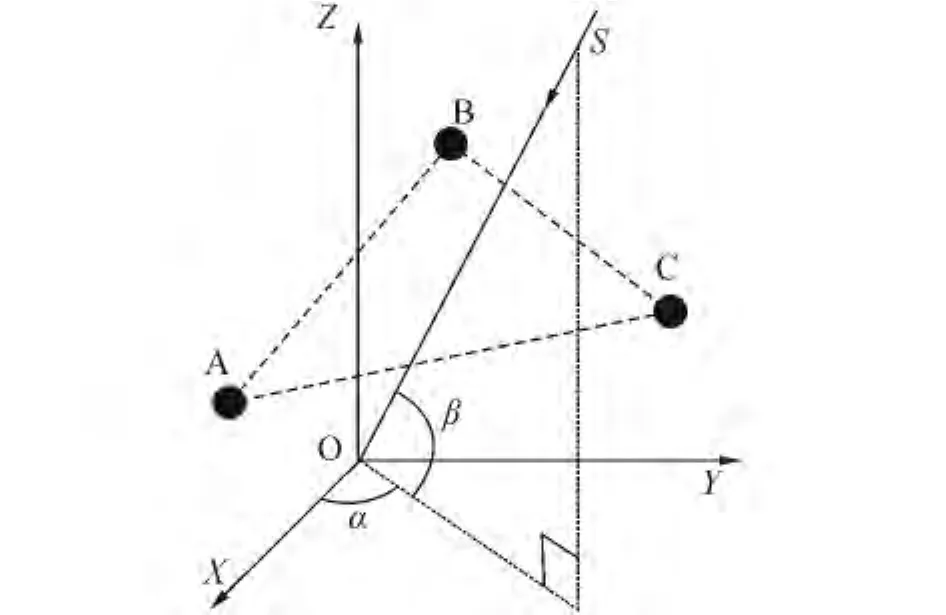
图2 任意基线模型Fig.2 Model of arbitrary baseline algorithm

假设不存在相位模糊，利用简单的几何关系，入射信号到达天线A、B、C的相位差可以表示为

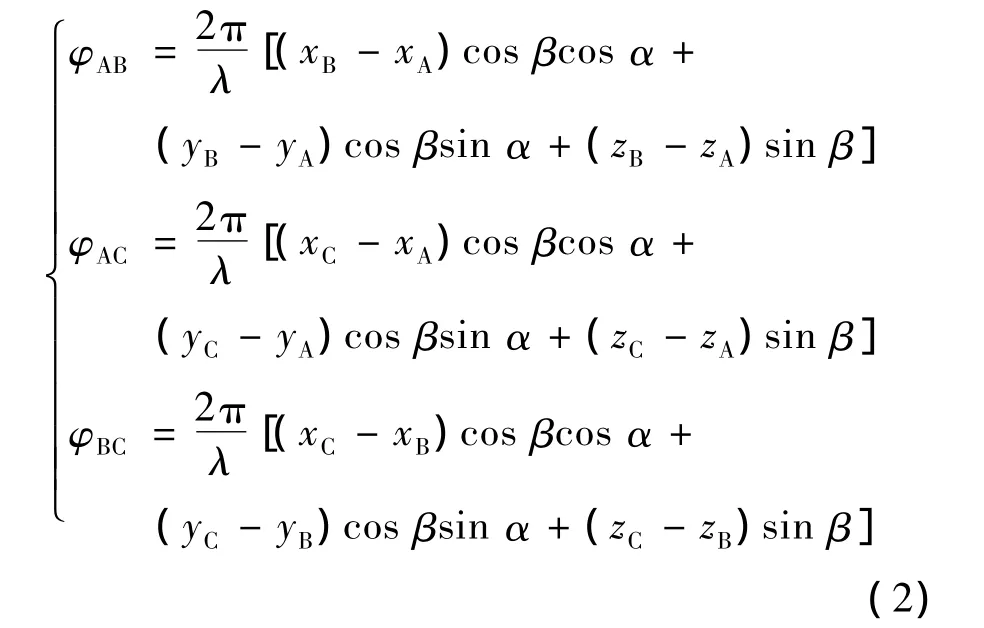
式中:φAB、φAC、φBC分别代表不同天线阵元之间的相位差。理论上，入射信号的角度信息可以通过求解式(2)中的任意2个得到。

考虑摆放在同一个平面的3个天线A、B、C，如图3所示。

考虑存在相位差的情况。入射信号到天线A、B、C的相位差简化为

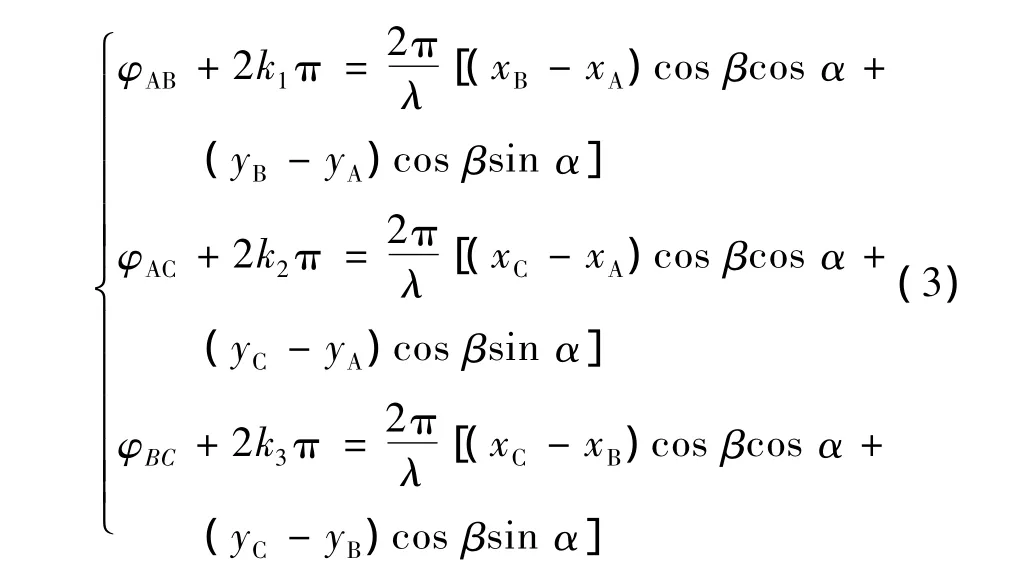
式中:k1，k2，k3=0，±1，±2···;tan α可以表示为

从式(4)中可以看出求得的入射信号角度存在镜像模糊，即如果tan α＞0，入射信号可能来自第一或第三象限;如果tan α＜0，入射信号可能来自其他2个象限。可以通过判断相位差的正负来得到入射信号的真实角度。从图3可以看出，如果φAB+2k1π＞0，入射信号来自第一象限，否则来自第三象限。tan α＜0时，判别方法相同。

从图3可以看出，任意基线算法的天线仍然摆放在同一平面内。主要原因是入射信号的角度信息包含在三角函数方程中，即式(3)。对于立体阵列，如式(2)，由于不存在解析解，必须像MUSIC算法那样去搜索角度。在频率很高时，由于非常多的模糊值存在，运算量非常大，因此很难在实际中应用。

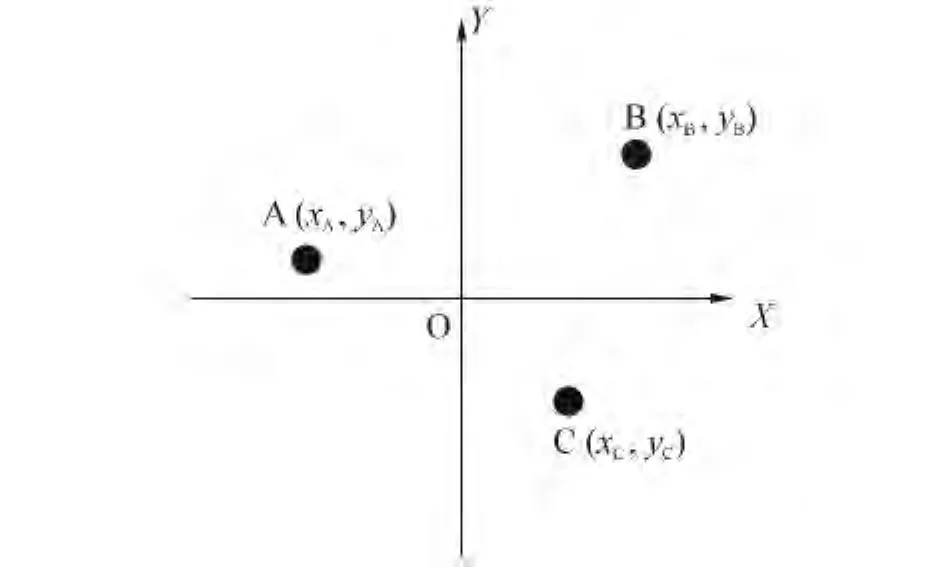
图3 天线阵元位置图Fig.3 The position of antenna elements

3 立体阵列任意基线算法

3.1 立体阵列任意基线算法测向原理

基于四天线的任意基线测向算法原理图如图4，这里D是摆放在空间的第4个天线，其他条件与图2相同。

入射信号到达4个天线的相位差为

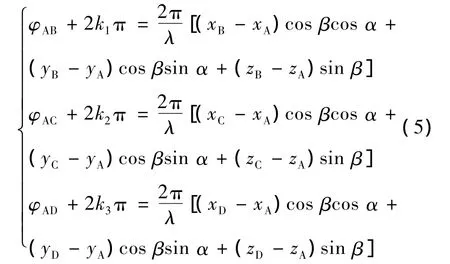
设 γ1=cos βcos α ，γ2=cos βsin α ，γ3=sin β 。把上式方程组转换成如下矩阵形式:

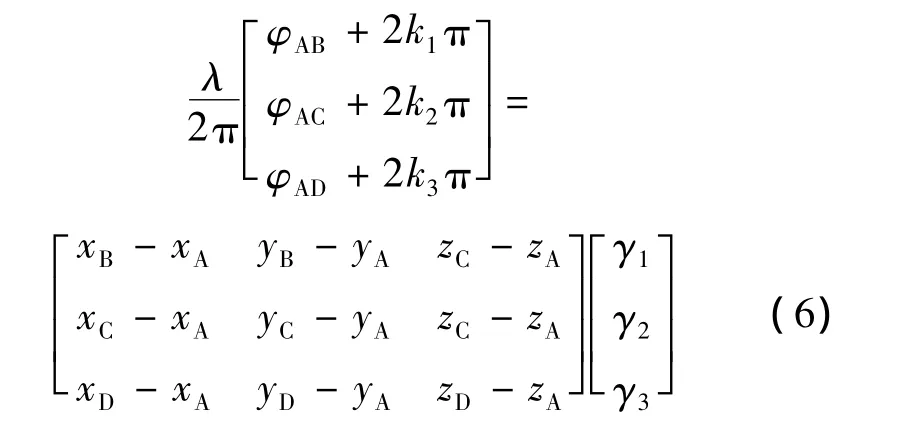
所以上述方程的解为

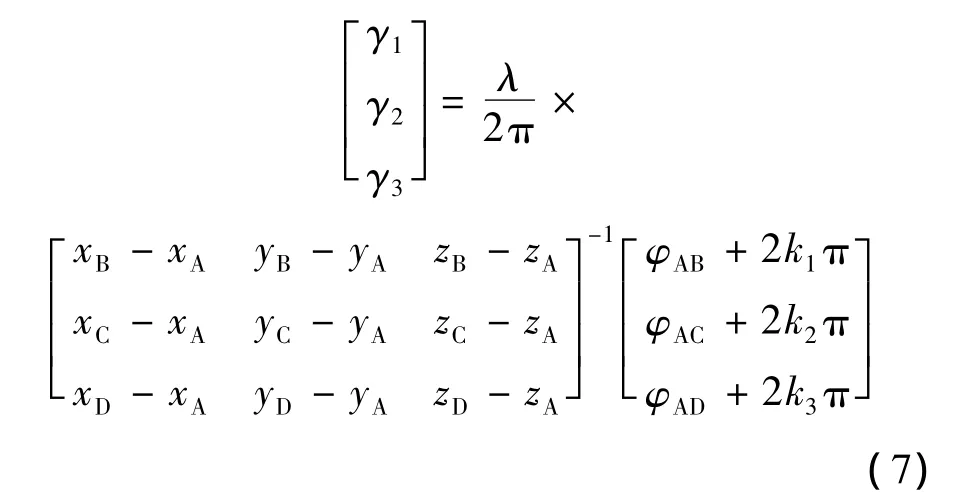
解得方程组后，分别得到 γ1、γ2、γ3三组值，求解 α、β有2种方法:

方法1:

方法2:

方法1中sin β的值域是 [0，1]，而在高频段，实际求得的γ3往往大于sin β的值域，无法得到正确的信号入射角，这是由于在高频段过多的模糊值造成的。所以本文采用方法2，由于tan α的值域是，所以它没有方法1中的限制，可以取到所有的角度，引入的误差也较小，这在解模糊过程中的比较带来了很大的方便。

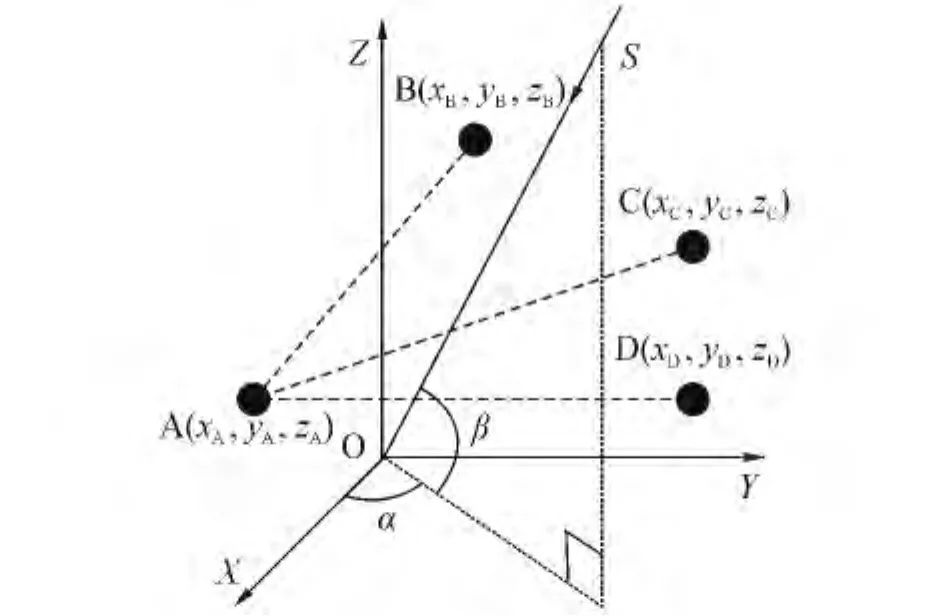
图4 四天线测向原理图Fig.4 The schematic of four antennas direction finding

3.2 基于虚拟基线方法的虚拟阵元

假设阵元E、F分别放置在Y轴和X轴上。M是另一个天线，利用阵元E、F构建虚拟阵元G、H的过程如图5所示。

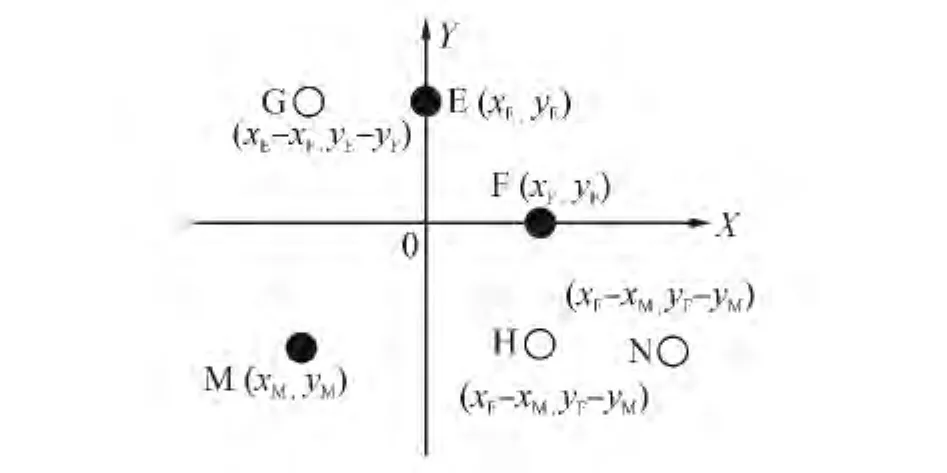
图5 虚拟阵元位置Fig.5 Positions of the virtual elements

利用任意基线算法的原理，阵元M、F和E、F的相位差可以写为

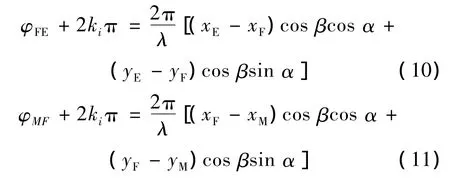
式中:ki=0，±1，±2···。式(10)、(11)左右两端同时相减，G和N的相位差可以写为

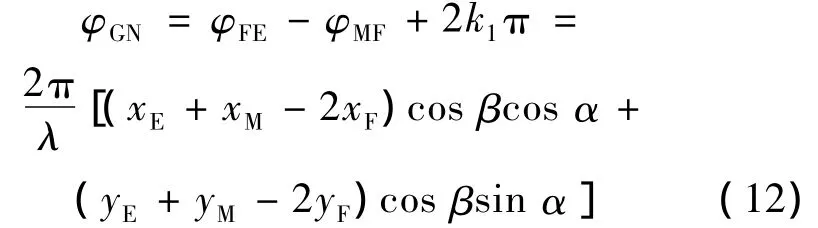
可以用式(12)代替式(5)中的任意一个方程来解式(7)。通过使用虚拟基线方法，阵元接收到的全部信息都能得到有效的利用。

3.3 基于轮换比对的解模糊方法

从任意基线算法的测向原理可知，摆放在空间的4个天线可以得到一组解。假设有n个天线，那么就有种基线组合。真实的入射信号角度包含在每一个基线组合里。通过比较每组基线中的模糊多值，每个基线中误差值最小的角度定义为真实信号的入射角度。

为了更清晰地阐述解模糊方法的原理，本文选择2组基线用来进行测向。2组基线的结果可以分别表示为[α1iβ1i]和[α2jβ2j]。2组测量结果之间的误差定义为

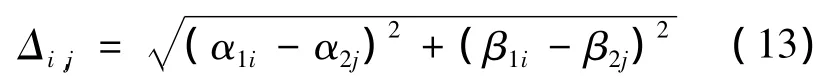
式中:i，j=1，2，3···，i和j分别代表第i个和第j个模糊值。真实的信号入射方向是使得式(13)取得最小值时的α和β。

在正确解模糊的情况下sin β、cos β的值域是[0，1]，所以只要判断 γ1、γ2的正负就可以判断α具体在哪一个象限，以便解镜像模糊。

4 改进的共形阵列天线算法

4.1 子阵分割技术

“阴影效应”是指由于金属遮挡，当入射信号从特殊角度入射的时候，不是所有的天线都能接收到信号。子阵分割技术的原则是对于入射信号来说，要确保至少有1个子阵能接收到信号。例如，对于柱面共形阵列天线来说，要保证每个子阵的覆盖范围大于π/2，如图6所示。图6中，1～4为4个真实阵元，摆放在第一象限的圆周上;a～k为虚拟阵元。假设有n个天线，那么有个利用虚拟基线方法构建的虚拟阵元。其中真实阵元和虚拟阵元都可以用来进行测向。

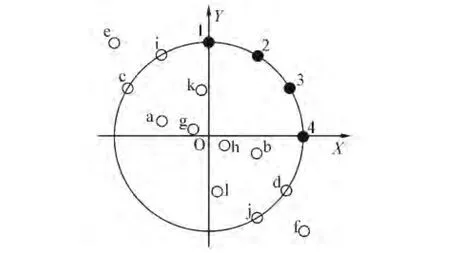
图6 扩展后的虚拟阵元位置Fig.6 Positions of the expanded virtual elements

4.2 算法步骤

利用虚拟基线方法和任意基线算法，求取入射信号角度信息步骤如下:

1)合理的安排共形在载体表面的共形阵列天线。每个子阵选择2组基线组合进行测向，4个天线构成一组基线组合(包括真实阵元和虚拟阵元);

2)通过求解式(8)、(9)，获得方位角α和俯仰角β。通过判断γ1、γ2的正负，镜像模糊可以得到解决，得到的所有模糊值作为第一组解;

3)对另一组基线组合，重复步骤2);

4)根据式(13)，得到入射信号的角度信息;

5)比较每个子阵获得的入射信号角度(由于“阴影效应”错误入射角度和真实入射角度之间会有很大差别)，各个子阵之间求得的最接近的角度值作为真实入射角度，进而求取其平均值作为最终信号入射方向。

5 仿真验证

12元均匀圆阵如图7(a)所示。每个象限中，4个LDPA共形在圆柱载体表面，如图7(b)所示。虚拟相位中心不在同一个平面内。忽略极化和互耦的影响。从图7可以看出，天线A1～A4构成4个真实阵元和10个虚拟阵元，它们可以划分为第1个子阵;同样天线A2～A5可以划分为第2个子阵，以此类推。使用子阵分割技术，12元天线阵列可以划分为9个子阵。

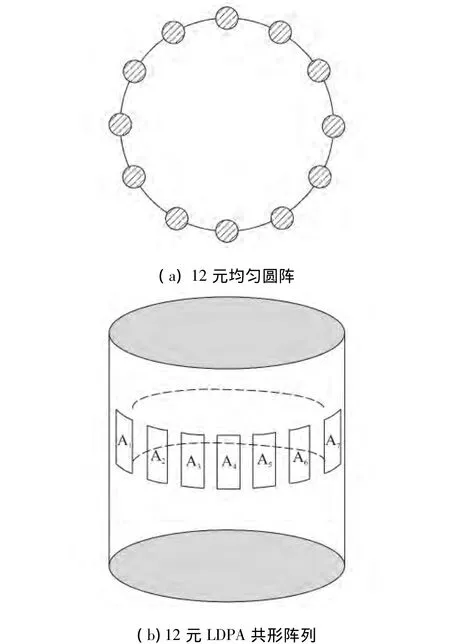
图7 天线摆放示意图Fig.7 Antenna placement

设定天线盘上天线可以利用的最大体积为半径r为200 mm的圆盘，天线模型如图7所示。辐射信号范围为1～15 GHz，选取实际信号入射信号方位角为45°，分别对仰角为60°和80°的情况进行仿真实验。

实验1 不同频率下解模糊概率比较。入射角度的俯仰角分别为β=80°和β=60°，信噪比为14 dB，相位差平均次数N=20，200次Monte-Carlo实验仿真结果如图8所示。从图8(a)中可以看出在辐射信号1～15 GHz范围内，立体阵列和平面阵列解模糊概率均在86%以上，解模糊概率高，验证了本文提出的方案可以实现宽频带范围内无模糊测向。比较图8(a)与图8(b)，可以看出在同样频率下β=60°时的解模糊概率小于β=80°时的解模糊概率，辐射信号到达天线的波程差在β=60°相对于β=80°更大，因此受更多的模糊值影响，解模糊概率相对较低。

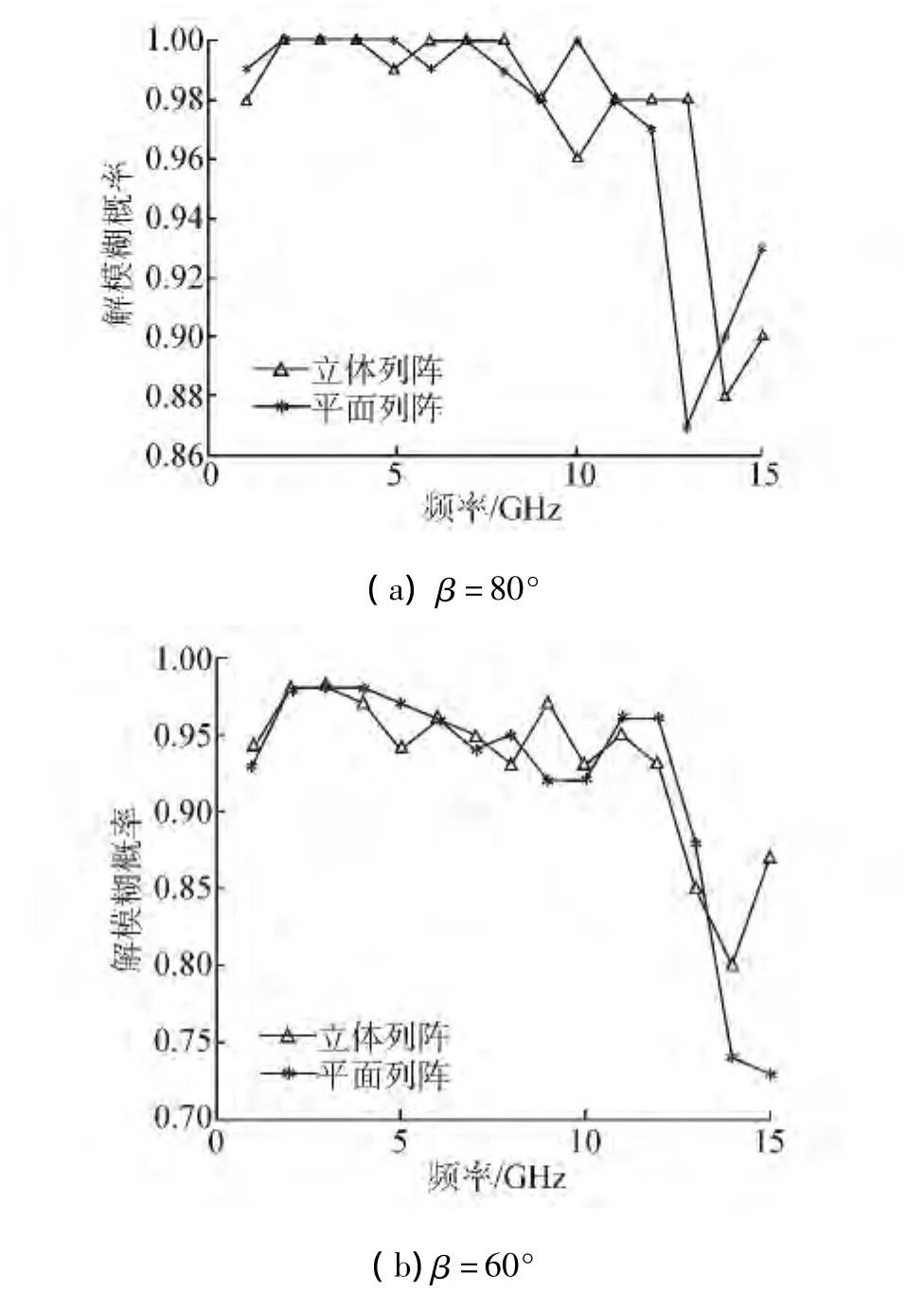
图8 不同频率下解模糊概率比较Fig.8 Comparison of solving ambiguous probability for different frequencies

实验2 不同信噪比下均方误差比较。入射角度的俯仰角分别为β=80°和β=60°，辐射源频率f分别为6 GHz和15 GHz，相位差平均次数N=30，200次Monte-Carlo实验结果如图9所示。可以看出随着信噪比的增大，平面阵列和立体阵列的均方误差都减小，增大信噪比可以提高2种阵列的测向精度。在相同信噪比的条件下立体阵列均方误差要稍大于平面阵列，但相差并不大。这是因为立体阵列在计算相位差时使用了多次的相位差加减运算，引入了误差。比较图9(a)、(b)，可以看出在β=60°均方误差相对较大，这是因为在β=60°时，天线之间的波程差相对较大，均方误差受到更多的模糊值的影响，导致测向误差增大。

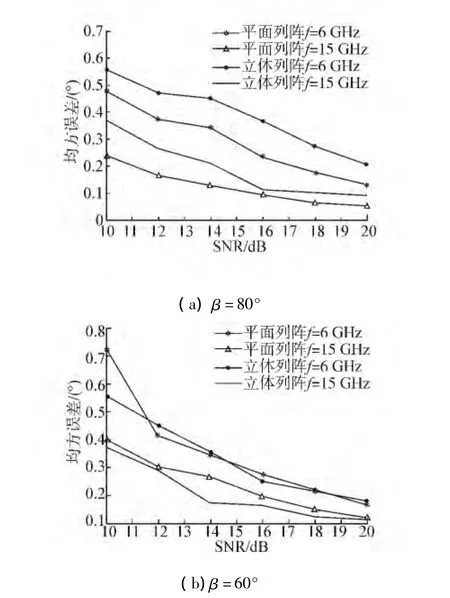
图9 不同信噪比下测向误差比较Fig.9 Comparison of direction finding error with different SNRs

实验3 不同方位角下均方误差比较。入射角度的俯仰角为β=80°，辐射源频率分别为6 GHz和15 GHz，信噪比为20 dB，相位差平均次数N=40，200次Monte-Carlo实验结果如图10所示。从图10中可以看出立体阵列和平面阵列在频率为15 GHz时的均方误差小于频率为6 GHz时的测向误差。两种阵列都是频率越高，均方误差越小。在相同方位角条件下，立体阵列和平面阵列的均方误差相差不大，均可以实现正确测向。

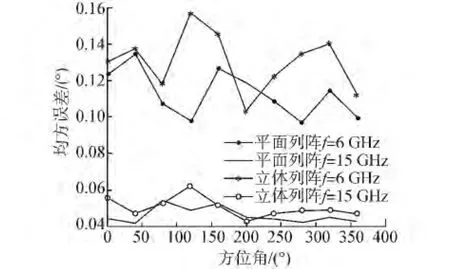
图10 不同方位角下测向误差比较Fig.10 Comparison of direction finding error with different azimuths

6 结论

1)本文提出了一种实时的超宽频带测向方法。利用任意基线算法和虚拟基线方法，结合子阵分割技术和矩阵求逆来获得入射信号角度信息。

2)4个天线作为一个基线组合，阵元不需要摆放在同一平面上。

3)所提算法测向误差和平面阵列的任意基线算法相差不大，适合于共形阵列天线的超宽频带测向。

4)本文不足之处:无法对多个信号同时进行角度估计，运算量相比平面阵列要大一些。

对所提算法解模糊概率和测向误差的理论分析，以及如何将所提算法应用到更复杂的载体上，在以后的工作中需要进一步深入研究。

［1］TSUI K M，CHAN S C.Pattern synthesis of narrowband conformal arrays using iterative second-order cone programming［J］.IEEE Transactions on Antennas and Propagation，2010，58(6):1959-1970.

［2］SOLIMENE R，DELL＇AVERSANO A，LEONE G.Interferometric time reversal MUSIC for small scatterer localization［J］.Progress in Electromagnetics Research，2012，131:243-258.

［3］LEE J H，JEONG Y S，CHO S W，et al.Application of the Newton method to improve the accuracy of TOA estimation with the beamforming algorithm and the MUSIC algorithm［J］.Progress in Electromagnetics Research，2011，116:243-258.

［4］YANG P，YANG F，NIE Z.DOA estimation with sub-array divided technique and interporlated esprit algorithm on a cylindrical conformal antenna array［J］.Progress in Electromagnetics Research，2010，103:201-216.

［5］Si W，WAN L，LIU L T，et al.Fast estimation of frequency and 2-D DOAs for cylindrical conformal array antenna using state-space and propagator method［J］.Progress in Electromagnetics Research，2013，137:51-71.

［6］LIANG J，LIU D.Two L-shaped array-based 2-d DOAs estimation in the presence of mutual coupling［J］.Progress in Electromagnetics Research，2011，112:273-298.

［7］HENAULT S，PODILCHAK S K，MIKKI S M，et al.A methodology for mutual coupling estimation and compensation in antennas［J］.IEEE Transactions on Antennas and Propagation，2013，61(3):1119-1131.

［8］SCHMIEDER L，MELLON D，SAQUIB M.Interference cancellation and signal direction finding with low complexity［J］.IEEE Transactions on Aerospace and Electronic Systems，2010，46(3):1052-1063.

［9］司伟建，初萍.干涉仪测向解模糊方法［J］.应用科技，2007，34(9):54-57.SI Weijian，CHU Ping.Research on the ways of solving direction finding ambiguous for interferometer［J］.Applied Science and Technology，2007，34(9):54-57.