基于反向试验信道的信息率失真函数计算方法

游雪肖，汪金汉

(湖北师范学院 数学与统计学院，湖北 黄石 435002)

基于反向试验信道的信息率失真函数计算方法

游雪肖，汪金汉

(湖北师范学院 数学与统计学院，湖北 黄石 435002)

利用Lagrange乘数法和互信息与熵的关系，提出了一种基于反向试验信道的信息率失真函数计算方法，给出了信息率失真函数的参量表示式，分析了该参量表示式中参数的物理意义，并举例说明了其具体应用.

信息论；反向试验信道；信息率失真函数；Lagrange乘数法

0 引言

在信息处理过程中，由于种种干扰因素的存在，不可避免地要丢失信息，产生失真。对于给定的信源，总是希望它的信息经过处理后所产生的平均失真在一定允许限度内的情况下，使得信源传输的信息率尽可能的小，这个最小值就是信息率失真函数R(D).一般可用Lagrange乘数法求解信息率失真函数，得关于试验信道亦即未知量{p(bj|ai)}的参量表示[1～5]，或先求出互信息I(X;Y)的最小值，然后从反向试验信道角度构造反向试验信道 {p(ai|bj)}证明最小值可达[6]，但反向试验信道的构造通常不是那么容易。本文利用互信息与熵的关系，从反向试验信道角度以{p(ai|bj)} 为未知量直接讨论R(D)的参量表示式以及参量S的物理意义。事实上，无论反向试验信道，还是正向试验信道，R(D)的参量表示式中参量S的意义是一样的，都是R(D)的斜率。从该方法还可以看出, 在信息率失真函数计算时，无论正向试验信道还是反向试验信道，都只是一个信道从两个不同角度考虑的两种不同表示方法而已，没有本质区别。

1 预备知识

定义1[1]信源X的熵定义为

信源X,Y的联合熵定义为

在给定信源Y的条件下，X的条件熵定义为

定义2[2]信源X,Y的互信息定义为

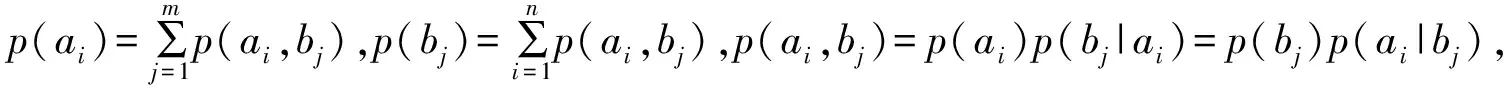
定理1[3]

I(X;Y)=H(Y)-H(Y|X)=

(1)

H(X)-H(X|Y)=

(2)

H(X)+H(Y)-H(X,Y)

(3)

定义3[2]对每一对(ai,bj)，指定一个非负函数d(ai，bj)≥0；i=1,2,…，n;j=1,2,…,m,称d(aj,bj)为单个符号的失真函数或失真度. 用它来表示信源发出一个符号ai，而在接收端再现bj所引起的误差或失真.

定义4[2]称

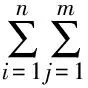
为信源的平均失真度．

定义5[2]离散无记忆信源的平均失真度如果不超过某一限定的值D，即Ed(X,Y)≤D，则称D是允许失真的上限.凡满足Ed(X,Y)≤D的 {p(bj|ai)}称为D失真许可的试验信道，简称试验信道．

定义6[2]信息率失真函数R(D)定义为

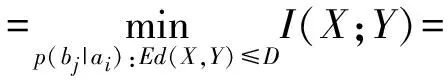
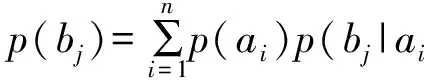
2 信息率失真函数的参量表示式

2.1问题的提出与转化

由定义6可知，信息率失真函数的计算实际上是求I(X;Y)在约束条件下的极小值问题，即

minI(X;Y)

(4)

在文献[1-5]中，R(D)的计算以{p(bj|ai)} 为未知量，利用Lagrange乘数法求解条件极值问题，从本质上都是利用式(1)，本文利用式(2)和(3)，以{p(ai|bj)} 为未知量，得到了关于反向试验信道{p(ai|bj)} 的信息率失真函数参量表示式.

2.2R(D)的参量表达式

为了在式(4)的 (n+2)个等式条件的限制下，求I(X;Y)的极值，可引入Lagrange乘数S、μ和αi(i=1,2,…，n)，利用式(3)构造一个新的函数

上式两边对p(ai,bj)求偏导数，并令其为0，即

(5)

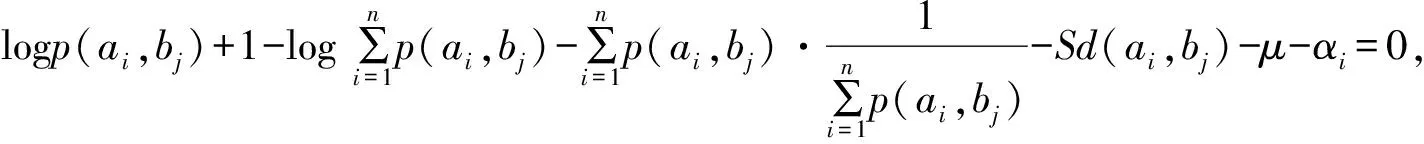
p(ai|bj)=eSd(ai,bj)βi,i=1,2,…,n;j=1,2,…,m.

(6)

上式两边对i求和并注意(4)式，有

(7)

(6)式两边同乘p(bj)，再对j求和，得

(8)

由(7)式解出βi，代入(6)式中得到p(ai|bj)，代入(8)式中得到p(bj)，将这些结果代入约束条件，可得

(9)

(10)

2.3参量S的意义

首先将R(D)对D求导数，则得

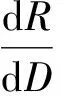
(11)

其次，在(7)式的两边对S求导数，可得

将上式两边乘以p(bj)，并对j求和，得

由此可见，在反向试验信道计算得到的信息率失真函数表示式中，参数S具有与正向试验信道中参数相同的意义。

2.4求解过程归纳

步骤如下：i)由(7)式求出βi；ii)由(6)式求出p(ai|bj)；iii)由(8)式求出p(bj)；iv)由(9)式求出D(S)；v)由(10)式求出R(D).

3 求解举例

设Y的概率分布为{q0,q1}，则由(8)式，得

因此，由(9)式得

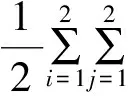
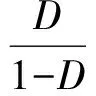
由(6)式，可计算得，

p(a1|b1)=p(a2|b2)=1-D,p(a2|b1)=p(a1|b2)=D

由(10)式，R(D)=I(X;Y)=H(X)-H(X|Y)=log2-H(1-D,D)

将该例与[1-5]比较可以看出，基于反向试验信道的信息率失真函数的计算要比[1-5]简单得多.

[1]曲 炜.信息论与编码理论[M].北京:科学出版社, 2005．

[2]陈 运.信息论与编码[M](第2版).北京: 电子工业出版社, 2007．

[3]叶中行.信息论基础[M](第2版).北京: 高等教育出版社, 2007.

[4]田宝玉.信息论基础[M].北京: 人民邮电出版社, 2008．

[5]王育民, 李 晖, 梁传军. 信息论与编码理论[M]. 北京:高等教育出版社, 2005．

[6]游雪肖，赵大方.等概离散无记忆信源率失真函数的计算方法[J].数学实践与认识，2014,44(10):163～168.

Acalculationmethodoftheratedistortionfunctionbasedonreversetestchannel

YOU Xue-xiao, WANG Jin-han

(College of Mathematics and Statistics, Hubei Normal University, Huangshi 435002, China)

Using the Lagrange multiplier method and the relationship of mutual information and entropy, this paper gives the parametric representation of calculating rate distortion function based on reverse test channel and analysis the meaning of the parameter. And gives an example of application.

information theory; reverse test channel; rate distortion function；Lagrange multiplier method

2014—04—18

游雪肖(1980— )，女，湖北襄阳人，讲师，硕士，主要从事信息论方面研究.

TN911;O171

A

1009-2714(2014)04- 0012- 05

10.3969/j.issn.1009-2714.2014.04.003