改进遗传算法在变形监测网平差中的应用

乐亚南,张献州,陈 超,2

(1.西南交通大学 地球科学与环境工程学院，四川 成都 610031; 2.中水成勘院测绘工程公司，四川 成都 610031)

改进遗传算法在变形监测网平差中的应用

乐亚南1,张献州1,陈 超1,2

(1.西南交通大学 地球科学与环境工程学院，四川 成都 610031; 2.中水成勘院测绘工程公司，四川 成都 610031)

遗传算法在处理非线性最小二乘问题上具有其独到的优势。文中通过对遗传算法的理论性研究，对常规遗传算法的选择交叉策略、变异步长及变异率都作了改进。并将改进的遗传算法应用到变形监测网平差中，实现变形监测网在不同基准下的非线性平差计算，并通过实例证明其实用性及优越性。

改进遗传算法；变形监测网；非线性平差；最小二乘准则

在处理变形监测数据的过程中大多数的数学模型都是非线性的，应用处理非线性问题的经典方法是将其线性化，近似值附近展开为泰勒级数，通常情况只取第一项，略去高级项[1-2]。而用这种近似的方法处理变形监测中精度要求非常高的数据，必然会使最后的成果质量下降，从而影响了变形监测数据的精度及可靠性。

随着测量技术的不断发展，用非线性方法处理变形监测数据已成为人们研究的热点。遗传算法是在1975年由美国Michigan大学J.Holland教授根据达尔文的进化论和G.Mendel的遗传变异理论提出的一种模仿生物进化规律的随机化搜索方法。这种算法在处理非线性数学模型上具有很好的效果。

针对常规遗传算法具有收敛速度慢、易陷入局部收敛等缺点以及变形监测数据对非线性平差形式的渴望，本文对常规遗传算法进行改进，并用实例验证了改进遗传算法在变形监测平差中的适用性及有效性。

1 改进遗传算法

遗传算法主要是以适应度来衡量解的优劣，在实际操作中，为了能够直观地反应个体对优化问题的解释程度，适应度函数一般是以目标函数的某种变换作为设计依据的，在进行时，种群中可能会产生适应度较强的个体而影响全局收敛。同时常规遗传算法变异步长是固定的，并具有随机性，这也可能造成收敛速度慢或得到较差的数据质量。针对常规遗传算法的以上缺点，从以下几点对遗传算法做了改进。

1.1 种群初始化

将种群规模设为m，基因(待估参数)个数设为n，问题解空间的下界和上界分别为Li和Ui，则初始种群的第i个个体编码如下：

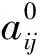
1.2 适应度函数的计算

适应度反应的是个体的适应情况，在计算时则需先构造适应度函数，合理的适应度函数可以使搜索向最优化方向发展。同时适应度函数是在非线性最小二乘平差准则VTPV=min的基础上求得的目标函数F(X)[3-4]。由于F(X)总是变化的，则存在区间[F(X)min,F(X)max]，并且目标函数是运用各个目标函数间的距离构造的。若个体i的目标函数值为F(Xi)，则个体i的适应度值为

式中：G(Xi)为个体i的适应度，ε为极小值。

1.3 选择与交叉

选择操作通常的做法都是采用轮盘赌的策略，这种方法虽然简单易行，但会产生“早熟”、“收敛速度慢”或是陷入局部收敛等问题[5]。本文采用一种最优化个体保护的策略[6]，通过某种方法判断种群中适应度最高的个体，不再经过遗传步骤直接复制两个该个体加到下一代种群，从而达到保护最优个体的目的。

常规遗传算法的交叉概率是不变的，这给遗传进化也带来了局限性，因此本文在交叉策略上采用的是动态自适应交叉率的方法和基于线性的快速寻优操作方法的改进方法。将二者的优点相结合保证了种群的多样性并且该算法可根据个体的适应度自适应调整，因此本文采用如下自适应交叉方案[7]：

其中：k1,k2是属于[0，1]之间的随机数;Gbig为交叉个体中适应度较大者;Gmax,Gavg分别为当代种群的最大适应度和平均适应度。

在交叉操作上，本文采用了一种基于线性的快速寻优操作方法[8]。

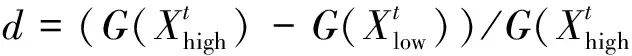
1.4 变 异

变异操作最主要的是可以维持种群进化过程中的多样性，并具有局部搜索能力，有效地防止陷入局部最优解的情况。变异操作的关键是变异步长和变异率[9]。

变异步长针对的是个体基因的变化，其取值伴随着一定的随机性，有时变异步长短会取得较好的优化效果，有时变异步长长会取得好的效果。针对步长的长短难确定的特点，采用自适应的随机变异步长，其公式如下：

式中:α的取值范围为[0，1]，Gen为遗传代数。

变异率对应的是种群，主要是与种群中变异种群的数目有关。变异率的大小决定了变异操作效果的好坏。因此本文采用的是自适应变异率方案，其公式如下：

式中:k1，k2是[0，1]间的随机数，Gmax为当代种群的最大种群数,Gavg为平均适应度，Gbig为交叉个体中适应度较大者，G为变异个体的适应度。

1.5 种群进化

在种群进行进化时，将t代种群和该种群经过交叉、变异产生的t+1代种群放在一起，将它们按适应度从大到小的顺序排列，取最优的前m-2个个体，再将适应度最强的两个个体复制两个一同放入下一代，并将后面的个体淘汰，这样种群就得到了进化。

2 改进遗传算法在变形监测中的应用

2.1 变形监测网的平差模型

在实际处理数据时，大多数的平差数学模型都是非线性的[10]，表达式如下：

L=f(X)+Δ.

其中:L表示m维观测向量，X表示n维待估参数向量，f(x)为X的非线性函数式，Δ为随机误差。在平差中，一般采用最小二乘原理来消除随机误差Δ的干扰，进而计算L的最佳估值[10]。变形监测网的非线性平差模型为

式中：Px为基准权方阵(变形监测主要应用固定基准、重心基准、拟稳定基准3个基准)，G为基准权的附加矩阵。要想将上式转化为标准的含有等式约束条件的优化问题，则可将变形监测网平差模型表示为

F(X)=VTPV=[f(X)-L]TP[f(X)-L].

并且满足

GTPxx=0.

应用以上两式就可以对附加基准方程的变形监测网进行平差优化。从而可解决非线性平差问题。

2.2 算 例

本文以一个测角网为例，验证改进遗传算法在变形监测网平差中应用的可行性，网图如图1所示。

图1 网图

图中A,B两点为已知点。坐标分别为A(4 628.4318，3 037.4051)，B(3 691.4417, 2 448.424 1)。方向观测值如表1所示。

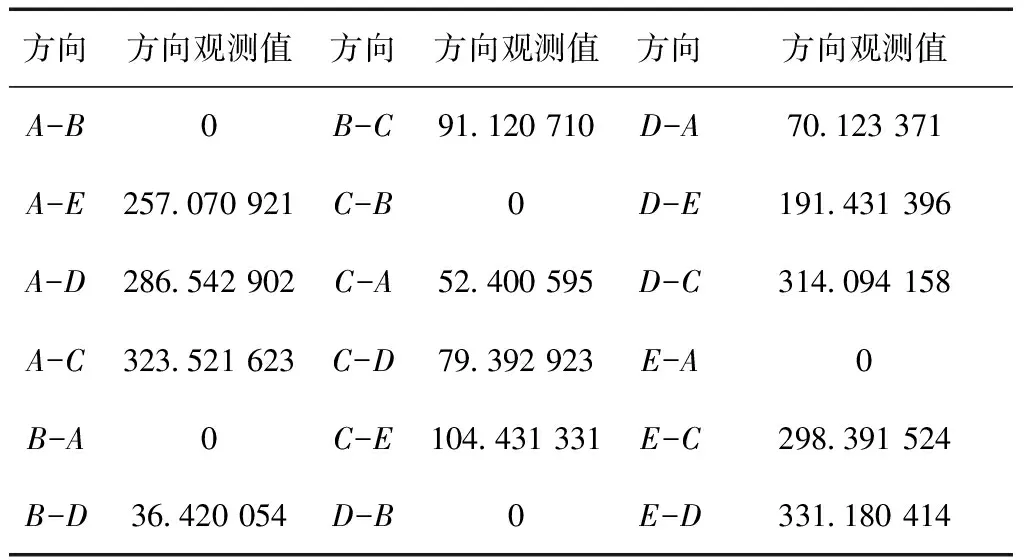
表1 方向观测值 (°)

各点的近似坐标如表2所示。

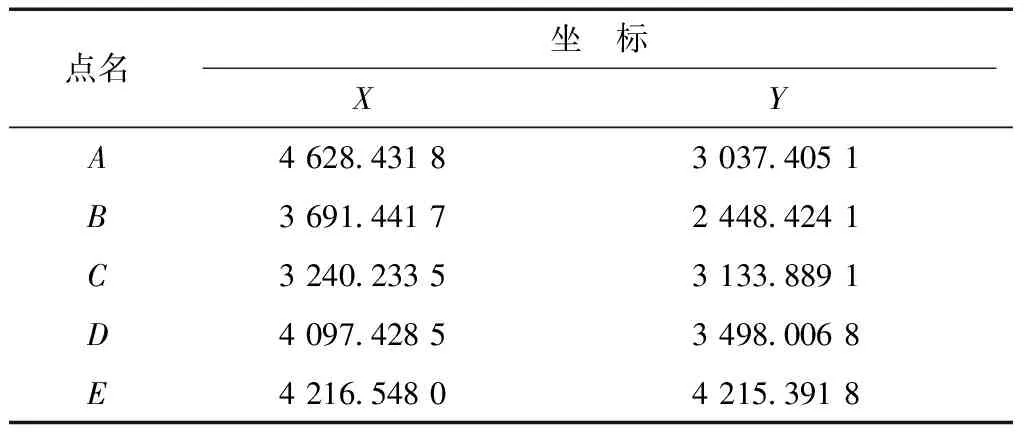
表2 各点的近似坐标 m

应用线性化法进行最小二乘平差后计算得到不同基准条件下各点的坐标,如表3所示。

表3 线性化方法平差计算的不同基准条件下各点的坐标 m

应用改进遗传算法平差后得到不同基准条件下各点的坐标,如表4所示。

表4 改进遗传算法平差计算不同基准条件下各点的坐标 m

在3种不同基准条件下，线性化方法与改进遗传算法各点坐标之间分别作差，结果如表5所示。

表5 线性化平差与改进遗传算法平差各点坐标之差 mm

从表5中可以看出，改进的遗传算法与线性化方法算得的固定基准的平差结果一致；重心基准平差的计算结果与线性化计算结果最大差值为0.56 mm；而拟稳重心基准的计算结果与线性化方法计算的结果最大差值为1.38 mm。在3种基准条件下，应用改进的遗传算法算得的最后结果与线性化平差基本一致，同时也证实了改进遗传算法在变形监测网平差中的可行性。

3 结束语

遗传算法是一种全局优化算法，尤其在非线性问题上具有明显的优势。本文在常规遗传算法的基础上进行了改进，采用了保存最优个体的选择策略，在交叉算法上采用了一种现行的快速寻优方法使适应度较弱的个体向适应度较强的个体进行基因的转化，防止了常规方法过早出现收敛的现象。为了满足实际工程上对非线性数据处理的实际需求，本文将改进的遗传算法与最小二乘平差准则相结合应用到了变形监测中。通过实例证明了改进的遗传算法在进行变形监测网平差方面具有较好的可行性及优越性。

[1]谷川，张岳. 遗传算法改进及其在非线性最小二乘平差中的应用[J].铁道勘察,2008(2):7-10.

[2]王穗辉.遗传算法在非线性最小二乘平差中的应用[J].大地测量与地球动力学,2006,26(2): 95-98.

[3]袁豹,岳东杰. 关于总体最小二乘方法适应性实验研究[J].测绘工程,2012,21(6):22-26.

[4]刘国林.非线性最小二乘与测量平差[M].北京：测绘出版社，2002.

[5]王越,许全文,黄丽丰.基于改进遗传算法的连续函数优化[J].重庆理工大学学报:自然科学版,2011,25(2):62-67.

[6]陈小平,于盛林.遗传算法交叉策略的改进[J].电子学报,2003,31(1)：1-4.

[7]朱灿.实数编码遗传算法机理分析及算法改进研究[D].长沙：中南大学,2009.

[8]陈小平,石玉,于盛林.快速寻优的遗传交叉策略[J].控制理论与应用,2002,19(6):981-984.

[9]陈超.实数编码遗传算法在变形监测网平差与变形预测中的应用[D].成都：西南交通大学,2012:34-40.

[10]田玉刚,王新洲,花向红.非线性最小二乘估计的遗传算法[J].测绘工程,2004,13(4):6-8.

[11]王新洲.非线性模型参数估计理论与应用[M].武汉：武汉大学出版社,2002.

[责任编辑：刘文霞]

Improved genetic algorithm applied to deformation monitoring network adjustment

LE Ya-nan1，ZHANG Xian-zhou1，CHEN Chao1,2

(1.School of Geosciences and Environmental Engineering Southwest Jiaotong University,Chengdu 610031, China; 2. Surveying and Mapping Engineering Co.,China Water Conservancy Survey and Design Institute, Chengdu 610031, China)

The genetic algorithm has its unique advantage in dealing with nonlinear least squares problems. Through the theoretical research of genetic algorithm, the selection and crossover strategy, mutation step size and mutation rates of conventional genetic algorithm are made with improvements. The improved genetic algorithm is applied to the deformation monitoring network adjustment in order to realize the nonlinear deformation covculation. The concrete example is demonstrated to prove its practicality and superiority.

improved genetic algorithm；deformation monitoring network；nonlinear adjustment；least squares criterion

2013-10-12

铁道部科技研究开发计划资助项目(2012G009-C);铁道部科技发展计划资助项目(2008G031-5);中央高校基本科研业务费专项资金资助项目(SWJTU10ZT02)

乐亚南(1987-)，女，硕士研究生.

P207

：A

：1006-7949(2014)10-0054-04