基于稀疏控制点的ZY-3影像几何纠正方法研究

刘 江，幸泽峰，刘丹丹

(1.黑龙江工程学院 测绘工程学院， 黑龙江 哈尔滨 150050； 2.中国科学院大学，北京 100049；3．中国科学院 东北地理与农业生态研究所，吉林 长春 130102)

基于稀疏控制点的ZY-3影像几何纠正方法研究

刘 江1，幸泽峰2,3，刘丹丹1

(1.黑龙江工程学院 测绘工程学院， 黑龙江 哈尔滨 150050； 2.中国科学院大学，北京 100049；3．中国科学院 东北地理与农业生态研究所，吉林 长春 130102)

研究在少量地面控制点情况下，利用仿射变换模型、多项式模型、有理函数模型对资源三号卫星(ZY-3)正视影像进行几何纠正。在无控制点参与精度评估情况下，提出利用几何纠正图与地形图叠合显示的方法评估几何纠正精度。研究表明：在少量分布合理的地面控制点下利用有理函数模型对ZY-3进行几何纠正，其几何纠正精度能达到后续应用的需求，具有一定的理论意义与实际应用价值。

资源三号卫星；几何纠正；仿射变换模型；多项式模型；有理函数模型

资源三号测绘卫星于2012年1月9日发射，是中国首颗民用高分辨率光学传输型立体测图卫星，集测绘和资源调查功能于一体，用于长期、连续、稳定、快速地获取覆盖全国的高分辨率立体影像和多光谱影像以及辅助数据，生产全国基础地理信息1∶5万测绘产品，开展1∶2.5万以及更大比例尺地图的修测和更新，并将为目前测绘地理信息行业的数字中国、天地图、监测地理国情3大平台建设提供自主高分辨率影像产品，同时也可以为国土资源调查与监测、防灾减灾、农林水利、生态环境、城市规划与建设、交通、国家重大工程等领域的应用提供服务。随着各种新型高分辨率卫星的出现，例如SPOT，IKONOS，QuickBird等高分辨率卫星出现时，国内外很多学者都对其影像数据的几何纠正进行了大量研究，基于各卫星的成像方式建立各种几何纠正模型。Muhammad Akbar和AN-Ming Wu在2006年提出像素投影方法，将每个像素利用一定数量的控制点进行投影，实现影像的几何纠正[1]；Marco Gaianinetto 提出基于无参算法自提取地面控制点卫星影像的几何纠正[2]；对于资源三号卫星，唐新明、高卫军、徐文、李德仁等对ZY-3数据进行了几何精度验证等相关几何研究[3-7]。本文旨在探求一种基于少量地面控制点的适合于ZY-3的几何纠正模型，并设计新的精度评价方法，评估不同模型的几何纠正结果精度，从而确定适合于ZY-3的纠正模型。

1 仿射变换纠正模型

仿射变换模型其实是基于平行投影的成像模型，它是利用仿射变换建立物方空间和平行投影影像面之间的数学关系,是一种线性模型。

Okamoto提出了一维和二维仿射变换模型[8]，以星载CCD传感器的飞行方向为中心投影影像坐标系的x轴，扫描方向为Y轴，则一维仿射变换算式为

(1)

第一个方程式建立了物方空间坐标系中的一个成像平面，第二个方程则体现了一维仿射影像与地面在O-YZ平面垂直投影之间的关系。

二维仿射变换模型克服了一维模型的一些不稳定缺点，其算式为

(2)

2 多项式纠正模型

多项式纠正模型回避成像的空间几何过程，直接对图像变形的本身进行数学模拟。多项式模型需要采集地面控制点，确定地面控制点后，需要读取所取控制点在图像上象元的图像坐标(x，y)以及它在参考系中的坐标(X,Y)。其变换式如下[9]：

(3)

式中：aij,bij是多项式的系数；X的次方数是多项式的次数，取值可以是1、2、3等，它是根据需要纠正图像的变形程度、地面控制点的数量以及地形位移的大小确定。一次线性多项式可以纠正6种几何变形，包括X，Y方向的平移、比例尺变形、倾斜和旋转。对于那些变形比较严重的遥感影像或者用户对精度的要求较高时，就需要采用二次或三次多项式。当多项式次数N确定以后，根据所选择的地面控制点的坐标，用最小二乘法回归求出多项式的系数，并完成对整幅影像的几何纠正。

3 有理函数纠正模型

有理函数模型在近几年应用广泛，有理函数模型实际上是带分式的多项式模型，它适用于各类传感器，包括最新的航空和航天传感器。像素坐标 (r,c)和像点对应的地物点在WGS-84坐标 (X,Y,Z)的有理函数模型[10-11]可表述为

(4)

式中：(r，c)和(X，Y，Z)一般是经过标准化后的无量纲坐标。标准化形式为

(5)

式中：Xraw等是原坐标值；Xoffset，Xscale等分别是平移参数与比例参数;X，Y，Z是标准化后的坐标值，其值在[-1，1]之间。这样做的目的是为了避免坐标值数量级差别过大引入舍入误差，提高计算精度。多项式Pi(X,Y,Z)(i=1,2,3,4)的一般形式为

(6)

每个P(X,Y,Z)是一个20项的三阶多项式：

Pi(X,Y,Z)=a0+a1X+a2Y+a3Z+a4XY+

a5XZ+a6YZ+a7X2+a8Y2+a9Z2+a10XYZ+

a11X2Y+a12X2Z+a13XY2+a14Y2Z+

a15XZ2+a16YZ2+a17X3+a10Y3+a10Z3.

(7)

式中的多项式系数ai称为有理多项式系数(Rational Polynomail Coefficients，RPCs)。在模型中由光学投影引起的畸变表示为一阶多项式，而地球曲率、大气折射及镜头畸变等改正可由二阶多项式趋近。高阶部分的其它未知畸变可用三阶多项式模拟。资源三号卫星影像采取类似IKONOS卫星的模式，为用户提供RPC系数。

4 几何纠正实验

4.1 实验数据

本次实验采用的是黑龙江省鹤岗市的ZY-3传感器校正产品，为正视全色影像，分辨率是2.1m，影像大小为50 km×50 km,其包括范围文件、影像体文件、元数据文件、浏览图文件、拇指文件(与浏览图类似)、RPC模型文件。

地面控制点数据用华测GPS测得，控制点的采集由于交通、经济等问题，具有一定困难。共测得9个地面控制点，有效点有7个，具有较高的精度。先是确定遥感影像的范围，再在Google Earth 中大致标注需要采集的点，这些点的特征比较明显，容易识别，其分布情况如图1～图2所示。

图1 控制点选点设计总体图

图2 控制点位分布图

4.2 实验结果

由于该影像的宽幅是50 km×50 km，范围过大，而且研究区域山区比较多，要取得足够的地面控制点有一定困难。因此，此实验在鹤岗市区范围内采集了少量的分布均匀的地面控制点。图3中，原始图像中的框出区域为研究区域，研究区域经裁剪后的图像见图4。

图3 裁剪范围

图4 裁剪区域图

3种模型纠正过程中都采用了7个地面控制点，多项式模型纠正时选用了一次多项式，纠正结果如图5所示。

4.3 精度评价

限于控制点的数量，本实验采取叠合地形图的方法。将各种几何纠正模型纠正结果与地形图辅助数据叠加显示，检查如栅格道路(或水系)与矢量道路(或水系)的吻合度，直观地评价各种纠正方法的几何精度。在叠合图中，均匀地选取了A-I共9处特征明显区域采用统一比例尺(1∶10 000)进行叠加比较，叠合情况如图6所示。

图5 几何纠正结果

图中线状矢量是道路信息，圆圈代表区域是所选择的精度评估区域，一共9处，均匀分布在图像中，A处对比图见图7。

图7中矢量为道路，箭头的长短表示矢量道路和栅格道路间隔大小，箭头越长，间隔越大吻合度越小；相反，箭头越短，间隔越小，吻合程度越大，几何纠正精度越高,以下组图类似。 B处对比见图8。

I处对比图见图9。

图6 叠合精度评估区域选取

图7 A处精度评估

图8 B处精度评估

图9 I处精度评估

通过这3组对比图可以看出：有理函数模型纠正结果栅格和矢量道路吻合度最好，仿射变换次之，其他6处精度评估情况大体类似。限于篇幅，文中只给出3处精度评估图，具体精度评价情况如表1所示。

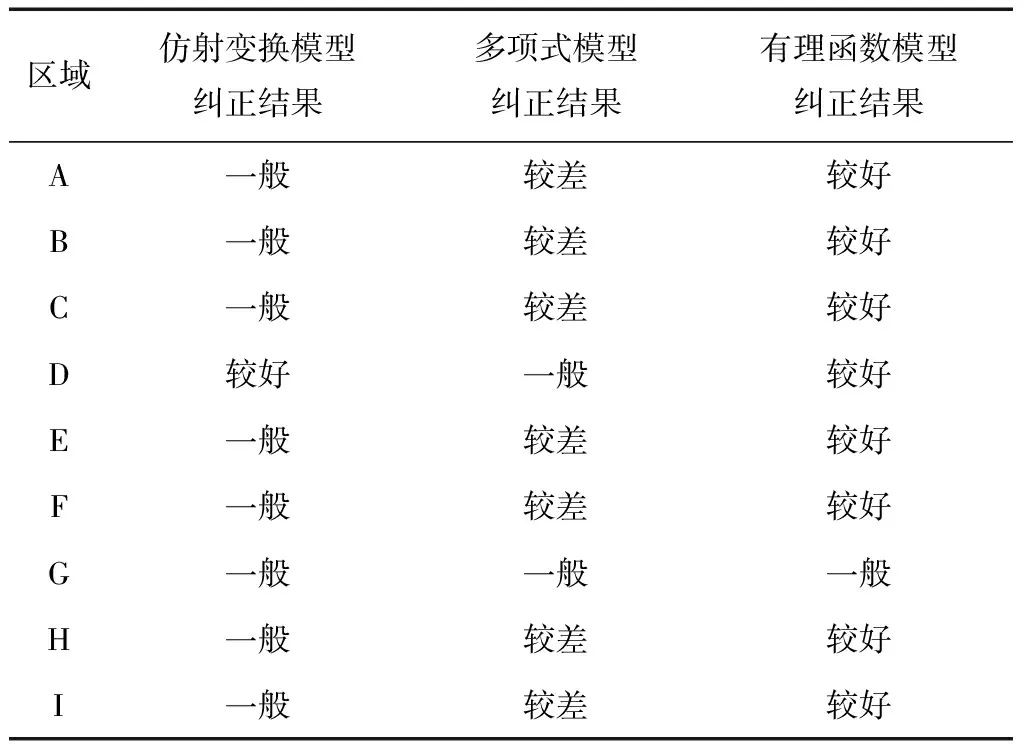
表1 精度评估表(吻合度)

所选取的9处精度评估区域均匀分布于纠正图像中，其评价结果具有整体代表性，故可以得出如下结论：基于稀疏控制点的有理函数模型纠正结果最吻合所提供的辅助地形图，精度最高；仿射变换模型纠正结果次之，精度一般；多项式模型纠正结果在几何上偏离程度最大，精度最差。所以在难于获得足够数量控制点情况下，资源三号卫星影像可以推荐使用有理函数模型进行几何纠正，能获得精度比较高的纠正结果。

5 结束语

针对国产高分辨率资源三号卫星正视影像的成像特点[12-13]，研究3种不同的几何纠正模型，并且主要研究基于稀疏地面控制点的情况下ZY-3影像的几何纠正方法和利用现有高精度地形图直观地评价其纠正精度。研究表明，利用有理函数模型的几何纠正结果与地形图的吻合度最高，其纠正效果最好，能达到后续应用研究的需求。因此，在少量分布合理的地面控制点的情况下，对ZY-3正视影像利用有理函数模型对其进行几何纠正，可以获得较高精度的纠正产品，为影像的后续应用提供更精准的服务。

[1]F ARIF, M AKBAR, An-Ming Wu. Geometric Correction of high resolution satellite imagery and its residual analysis [J].2006: 162-166.

[2]M GIANINETTO, M SCAIONI. Satellite images geometric correction based on nonparametric algorithms and selfextracted GCPs[C].Geoscience and Remote Sensing Symposium,20-24 sept,2004: 3755-3758.

[3]巩丹超，张永生.有理函数模型的解算与应用[J].测绘学院学报, 2003,20(1): 39-42.

[4]唐新明，张过,祝小勇,等.资源三号测绘卫星三线阵成像几何模型构建与精度初步验证[J].测绘学报，2012,41(2): 191-198.

[5]高卫军，孙立，王长杰,等.“资源三号”高分辨率立体测绘卫星三线阵相机设计与验证[J].航天返回遥感，2012, 33(3): 25-34.

[6]徐文，龙小详，喻文勇，等.“资源三号卫星”三线阵影像几何质量分析[J].航天返回与遥感，2012, 33(3):55-64.

[7]李德仁，王密.“资源三号”卫星在轨几何定标精度评估[J].航天返回与遥感,2012,33(3):1-6.

[8]A OKAMOTO, T ONO, ect. Geometric Characteristics of Alternative Triangulation Models for Satellite Imagery[C].ASPRS 1999 Annual Conference Proceedings. Oregon:1999.

[9]孙家抦.遥感原理与应用[M].武汉:武汉大学出版社,2009.

[10]郑琳，陈鹰，林怡. SPOT影像的RPC模型纠正[J].测绘与空间地理信息，2007,33(2):16-19.

[11]方铮，葛洁，王勇.基于SPOT5卫星遥感数据的正射影像生产技术研究[J].测绘工程，2012，21(3)：58-62.

[12]温礼，程博，柴渊，等.SAR遥感数据监测土地利用变化的研究[J].测绘科学，2014，39(6)：65-69.

[13]张万强，赵俊三，唐敏.无人机影像构建三维地形研究[J].测绘工程，2014，23(3)：36-41.

[责任编辑：张德福]

Research on geometry rectification method of ZY-3’s image based on sparse control points

LIU Jiang1, XING Ze-feng2,3, LIU Dan-dan1

(1.School of Surveying and Mapping Engineering, Heilongjiang Institute of Technology, Harbin 150050,China;2.University of Chinese Academy of Sciences, Beijing 100049,China;3.Northeast Institute of Geography and Agroecology, Chinese Academy of Sciences, Changchun 130102, China)

It uses the affine transform model, polynomial model,and rational function model for geometric correction for ZY-3’s front view image in the case of a small amount of ground control points.Under the condition of no control points in precision evaluation,a method of using the corrected images with the topographic map composite shows is used to assess the precision.The study shows that under the condition of rational distribution of a small amount of ground control points,the result of using rational function model for ZY-3’s image can meet the demand of subsequent application.And the research has certain theoretical significance and practical application value.

ZY-3 satellite; geometric correction; affine transformation model; polynomial model; rational function model

2013-08-23，2014-07-28补充更新

黑龙江省自然科学基金资助项目(E201203)；黑龙江工程学院青年基金项目(2013QJ05)

刘 江(1980-)，男，讲师.

P236

：A

：1006-7949(2014)10-0036-05