平息债券估价模型的比较分析与扩展
2014-08-22韩建丽杨位留
韩建丽,杨位留
(枣庄学院 经济与管理学院,山东 枣庄 277160)
0 引言
债券估价,即债券内在价值的计算,是债券发行者确定债券发行价格和债券投资者确定债券购买价格的参照,对于发行者和投资者都至关重要,因此债券的估价问题受到了财务管理学者的广泛关注.债券估价的基本原理是按投资者要求的必要报酬率作为贴现率来贴现债券预期在未来所产生的全部现金流量.[1]
债券利息的支付有多种方式.其中,平息债券是指利息在到期时间内平均支付的债券,其支付的频率可能是一年一次、半年一次或每季度一次等.其中,利率固定,每年付息一次,到期还本的债券又被称为典型债券.对于典型债券的估价模型学者们的观点一致,如公式(1)所示:
PV=M×i×(P/A,K,n)+M×(P/F,K,n)
(1)
然而,对于一般的平息债券的估价模型争议较大,当前,主要有以下三种估价模型:

(2)

(3)

(4)
在上述公式(1)—(4)中,PV代表债券价值,M 为债券面值,i 为债券的票面年利率,K为投资者要求的年必要报酬率,n为债券的存续年限,m为债券的年付息次数.
模型1是注册会计师考试《财务成本管理》教材中采用的模型[2],模型2是中级会计师资格考试《财务管理》教材中采用的模型.[3]从查阅的众多文献中也可以得知,这两种模型是当前众多财务学者普遍认可的.模型3是少数学者坚持的观点[4,5],当前并未得到普遍重视.本文将对这三种模型进行比较,以期找到最恰当的平息债券估价模型.
1 平息债券估价模型的比较分析
1.1 一年内付息多次的情形
我们对平息债券估价的三个模型进行比较,模型1和模型2的差别在于对债券面值的折现采用的折现方法不同,而模型2与模型3的差别在于对债券利息折现采用的折现率不同.为了使模型的比较更加直观,下面结合实例进行分析.
例1: 甲公司拟发行债券进行筹资,现有两个方案:A方案每年付息一次,B方案每半年付息一次,除此之外两个方案的其他条件均相同.债券面值均为1000元,6年期,票面利率为8%,到期还本,投资者要求的必要报酬率为10%.要求对A、B两个方案的债券进行估价.
A方案的债券为典型债券,其价值计算简便,并无异议.计算过程如下:
PVA=1000×8%×(P/A,10%,6)+1000×(P/F,10%,6)=912.9(元)
B方案的债券是平息债券,债券的年付息次数为2,其价值计算有下列三种方法:



B方案相对于A方案而言,从企业的角度,还本付息的总额不变,但付息的次数更为频繁,相关成本增加,要求筹集到更多的资金来弥补,因而债券的价值应该略高;从投资者的角度,获得的现金流入总额不变,但每年有部分利息提早流入,可用于再投资,从而债券价值也应该略高.
表1列示了A、B方案债券的现金流量及其差量现金流量,对B方案与A方案债券的差量现金流量进行折现,无论采用的折现率如何,其净现值始终为正值,从而从数量上也证明了B方案债券的价值应大于A方案.然而,根据模型1计算出的B方案债券的价值为911.4元,小于A方案债券的价值912. 9元,很显然模型1的计算方法是不合理的.

表1 A、B方案债券的现金流量及其差量现金流量
根据长期投资决策中的互斥方案现金流量净现值的差额等于其差量现金流量的净现值的原理进行分析,B方案债券的价值减去A方案债券的价值应该等于它们的差量现金流量的净现值.模型2与模型3的差异在于对利息进行折现采用的折现率不同,模型2采用的是10%/2=5%,即假设投资者要求的必要报酬率为名义值;而模型3采用的是(1+10%)1/2-1=4.8809%,即假设投资者要求的必要报酬率为实际值.
根据模型2,结合上述分析,利用差量现金流量的原理,计算:B方案与A方案价值的差量=B方案债券的价值-A方案债券的价值=919.0-912.9=6.1(元)
B方案债券与A方案债券差量现金流量的净现值为:
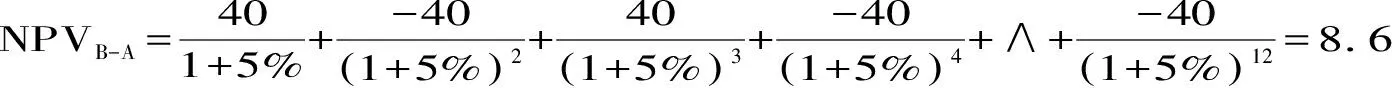
二者的计算结果并不相等,可以看出模型2的算法不合理.
同理,根据模型3计算:B方案与A方案价值的差量=B方案债券的价值-A方案债券的价值=921.4-912.9=8.5(元)
B方案债券与A方案债券差量现金流量的净现值
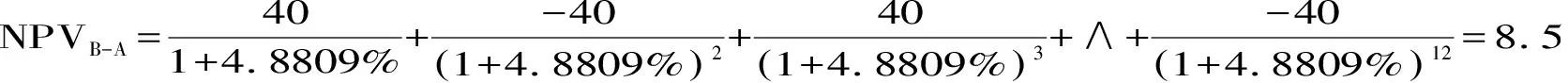
二者计算结果相等,模型3的算法是合理的.
上述计算结果不难理解,投资者在进行投资时,真正关注的是实际收益而不是名义收益.对投资者来说,如果要求年实际收益率为10%,根据复利计息原理,半年获得(1+10%)1/2-1=4.8809%的收益即可.
上述实例是债券的票面利率小于投资者要求的必要报酬率的情况,若票面利率大于投资者要求的必要报酬率的情况,同样可以得出模型3的合理性,这里不再赘述.
1.2 债券超过一年付息一次的情形
根据上述结论,债券一年内付息多次,即m大于1时,使用模型3对债券进行估价是合理的.下面我们再来检验超过一年付息一次的债券,即m小于1时,利用模型3进行估价的合理性.
例2:承接例1,假设甲公司同时还拟定了方案C,每两年付息一次,其他条件均相同.此时一年付息次数m应为0.5.
按照模型3,C方案债券的价值计算如下:

C方案债券的价值-A方案债券的价值=896.3-912.9=-16.6(元)
由于在第1—6年末,A方案债券的现金流量为80、80、80、80、80、1080,C方案债券的现金流量为0、160、0、160、0、1160,因此差量现金流量(C-A)为-80,80,-80,80,-80,80.C方案债券与A方案债券差量现金流量的净现值

从上述计算结果看,对于超过一年付息一次的情形,模型3也是恰当的估价方法.
综上,对于平息债券的估价,使用模型3,即债券价值的计算按照复利原理算出的实际期间必要报酬率作为折现率进行折现的方法是最为合理的.
2 平息债券估价模型的扩展
事实上,债券估价模型3除了可以写成上述公式(4)的形式外,还可以写成公式(5)
(5)
从公式(5)可以看出,平息债券的估价与其他类型债券的估价相似,只需要将现金流量按照投资者要求的年必要报酬率向前折算相应的年数即可.如例1中方案B的债券,分别在0.5年、1年、1.5年、2年、2.5年、3年、3.5年、4年、4.5年、5年、5.5年、6年有40、40、40、40、40、40、40、40、40、40、40、1040这12个预期现金流量,只需要将它们按照10%的必要报酬率依次向前折算对应的年数即可得到方案B债券的价值.
由此,可以总结出一个适合任意偿本付息方式下债券的估价模型:
(6)
公式(6)中,PV为债券价值,N为债券预期现金流量(即本息和)的个数,Cj为第j个预期现金流量(即本息和)的值,tj为第j个预期现金流量(即本息和)距离债券估价这一时点的年数,K为投资者要求的年必要报酬率.
现举例说明公式(6)的普遍适用性:
1.典型债券.如例1的方案A的债券.N=6,C1=C2=C3=C4=C5=80,C6=1080,t1=1,t2=2,t3=3,t4=4,t5=5,t6=6,K=10%.
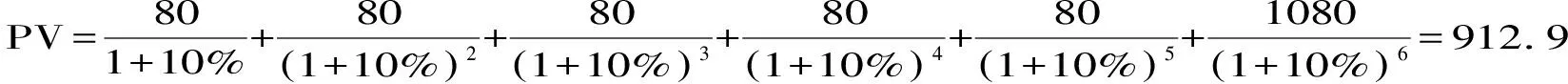
2.平息债券.如例1的方案B的债券.N=12,C1=C2=C3=……=C11=40,C12=1040,t1=0.5,t2=1,t3=1.5,t4=2,……,t12=6,K=10%.
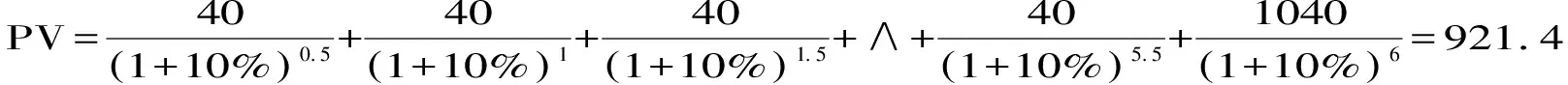
3.零息债券.假设有一零息债券,面值1000元,20年期,折现率为10%,求债券价值.则此时N=1,C1=1000,t1=20,K=10%.

4.到期一次还本付息债券.假设有一5年期债券,面值1000元,票面利率12%,到期一次还本付息,折现率为10%,求债券价值.则此时N=1,C1=1000+1000×12%×5=1600,t1=5,K=10%.

5.流通中的债券.假设有一面值为1000元的债券,票面利率8%,2011年5月1日发行,2016年4月30日到期,每年4月30日,10月30日支付一次利息,现在是2014年3月1日,折现率为10%,计算该债券价值.则此时N=5,C1=C2=C3=C4= 1000×8%/2=40,C5=1040,t1=1/6,t2=2/3,t3=7/6,t4=5/3,t5=13/6,K=10%.

3 结语
本文结合实例,依据投资决策中的现金流量净现值的差额等于其差量现金流量的净现值的原理对债券估价模型进行了比较分析,从分析的结果看,债券本息按照根据复利原理计算出的实际期间必要报酬率作为折现率进行折现的方法是科学合理的.基于该方法,对估价模型做了一步扩展,得出适合任意偿本付息方式下的债券估价模型,使其应用范围更加广泛.
[1]张功富,索建宏.财务管理原理(第2版)[M].北京:首都经济贸易大学出版社/中国农业大学出版社,2011:116-117.
[2]中国注册会计师协会.财务成本管理[M].北京:中国财政经济出版社,2013:111-115.
[3]王志伟.会计师和CPA考试财务管理教材的不同观点[J].财会月刊,2012,(17):63-65.
[4]任汝娟.平息债券估价模型再修订[J].财会月刊,2006,(6) :80.
[5]程养林.平息债券估价模型优化方案研究[J].商业会计,2011,(34) :22-23.
