再谈数列不等式的解决策略
2014-08-22安徽省六安市金安区教育局邮编237000
安徽省六安市金安区教育局 (邮编:237000)
文[1]从证明的视角阐述了解答题中数列不等式的一些经典证法,所选例题具有很好的代表性,所选方法具有普适性、思想性,方法的分析简明而深刻,笔者读后很受启发,也引发了笔者对数列不等式问题的进一步思考:实际上,数列不等式问题并非只有证明这一类问题,求解型数列不等式问题也占有一席之地,有时甚至较证明型问题更加难以解决,原因主要是求解型数列不等式一般没有明确的解题目标,需要深入地探索,对学生的知识与经验形成极大的挑战;至于数列不等式的证明也绝非只有文[1]所提供的这几种证法. 文[1]在以上问题上没有涉及,作为对文[1]的补充,本文以近三年全国及各省部分数列解答题为例,对以上问题作分析与总结,供大家参考.
1 注重不等式知识运用
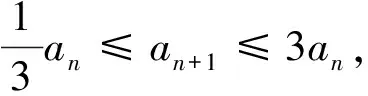
(Ⅰ)若a2=2,a3=x,a4=9,求x的取值范围;
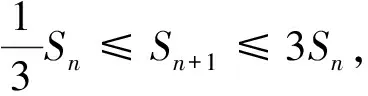
(Ⅲ)若a1,a2,…,ak成等差数列,且a1+a2+…+ak=1000,求正整数k的最大值,以及k取最大值时相应数列a1,a2,…,ak的公差.
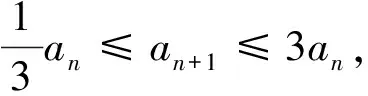
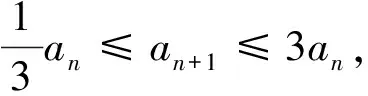
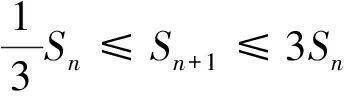
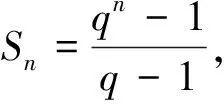
因q>1,故3qn+1-qn-2=qn(3q-1)-2>2qn-2>0.
对于不等式qn+1-3qn+2≤0,令n=1,得1≤q≤2,当1 故qn+1-3qn+2=qn(q-3)+2≤q(q-3)+2=(q-1)(q-2)≤0, 故1 例2(2012重庆卷理21)设数列{an}的前n项和Sn满足Sn+1=a2Sn+a1,其中a2≠0. (Ⅰ)求证:{an}是首项为1的等比数列; (*) 当a2=1时,上式等号成立. 评注上述证明过程中,想到 例3(2012安徽卷理21)数列{xn}满足n∈N*. (Ⅰ)证明:{xn}是递减数列的充分必要条件是c<0; (Ⅱ)求c的取值范围,使{xn}是递增数列. 分析数列单调性最常用的判断方法是定义,而定义本身具有充要性,即等价性. 所以用等价转化可以减小本题难度. 略解(Ⅱ)当数列{xn}是单调递增数列时,xn+1>xn≥x1=0恒成立. xn+2-xn+1=-(xn+1-xn)(xn+1+xn-1)>0 ⟺xn+1+xn-1<0. 知xn+1+xn-1<0成立; 例4(2014重庆卷理22)设 (Ⅰ)若b=1,求a2、a3及数列{an}的通项公式; (Ⅱ)若b=-1,问:是否存在实数c使得a2n 分析“存在型”问题一般都应从假设结论成立开始考虑(即考虑结论成立的必要条件),先用特殊情况把待求值“逼”出来,但考虑本题中的递推式较复杂,不可能求出通项,因此,只能考虑极限(不等式两边都是项,且相邻)两边夹出c. 下面可用数学归纳法证明加强命题:a2n 评注本题中的c来自于下列极限思想:若a2n 例5(2014安徽卷理21)设实数c>0,整数p>1,n∈N*. (Ⅰ)证明:当x>-1且x≠0时,(1+x)p>1+px; (Ⅱ)数列{an}满足 例6(2012广东卷理19)设数列{an}的前n项和为Sn,满足2Sn=an+1-2n+1+1,n∈N*,且a1,a2+5,a3成等差数列. (Ⅰ)求a1的值; (Ⅱ)求数列{an}的通项公式; 分析(Ⅲ)中的不等式右边是常数,无法实现归纳递推,所以数学归纳法不好使用(但并不是不能使用,只是技巧性强),本题使用了特殊的放缩法. 略解(Ⅲ)因为an=3n-2n=3(3n-1-2n-1)+(3·2n-1-2n)=3an-1+2n-1 评注间接放缩主要采取一种整体思维,本题中Sn的范围不是直接放缩出来的,而是将Sn当成整体,通过“递推式放缩”得到关于Sn的不等式,进而解出要证的不等式. 这种“递推式放缩”可以有效解决“和式小于常数”的不等式,弥补数学归纳法不足. (Ⅰ)讨论f(x)的单调性; 分析本题以函数为背景,考查数列问题. 但(Ⅱ)中到底要用函数的哪个形式,需要结合待证不等式从单调性中自行寻找. 评注借助函数不等式证明数列不等式,其关键还是找到合适的函数,以及选取此函数合适的特殊情形,两者缺一不可. 如何能够有效地做到呢?笔者认为,积累解题经验和善于分析待证数列不等式特征是不可或缺的. 故fn+1(xn)>fn(xn)=fn+1(xn+1)=0,由第(Ⅰ)问知fn+1(x)在(0,+∞)上递增, 得xn+1 ① ② 评注本题方法充分体现了回归定义的重要性. 实际上,广大考生曾绞尽脑汁试图想出妙法都未成功. 当然,成功整理“和式”并利用有界性放缩也是关键一步. 从以上几例的分析、评注可以看出,数列不等式由于具有数列和不等式的“二重性”,因而其解决方法应与二者息息相关. 如,数列是特殊的函数,因而函数的一切方法都可以考虑应用于数列不等式:单调性、有界性、极限、零点、不动点等;数列与正整数有关,因而数学归纳法、递推、迭代等也可使用;数列有通项公式、前n项和公式,因而通项分析、前n项和分析也是必备手段. 至于不等式,有基本性质、重要不等式模型等,它又可以营造出千变万化的不等式技巧,如传递性就是放缩法的理论依据;不等式既可求解也可证明,它们的方法又可以迁移到数列不等式中来,如分析法,等等. 总之,以上只是结合近三年高考考题作了一番梳理,实际上,数列不等式类型多种多样,其解决策略亦多种多样,有时呈现单一性,有时呈现复合性,相信它还会随着高考新题的出现继续演绎着更迷人的精彩. 1 章政权.例说数列不等式的证明[J]. 中学数学教学,2014(4):45-48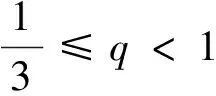
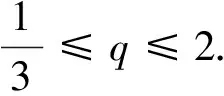
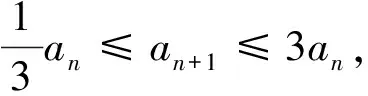
2 注重分析法分析功能


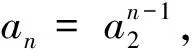

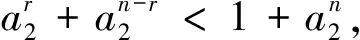

3 注重等价转化思想运用

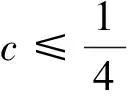

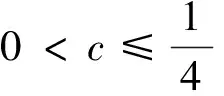
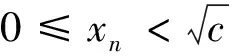
4 注重高等数学知识背景
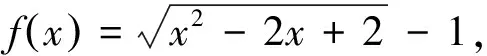
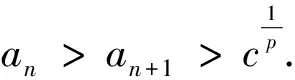


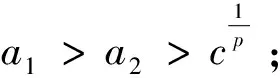

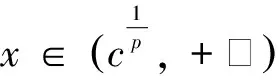


5 注重间接放缩法的使用
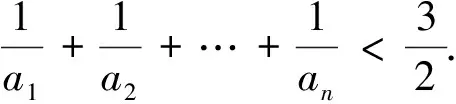
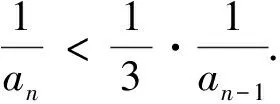



6 注重利用数列的函数性

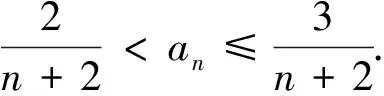


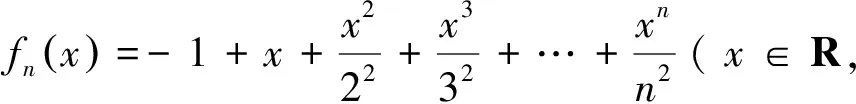
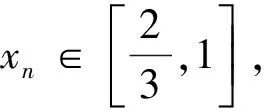
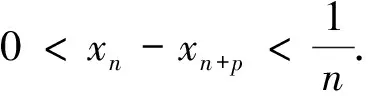
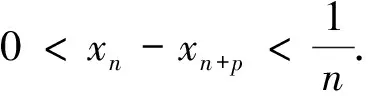
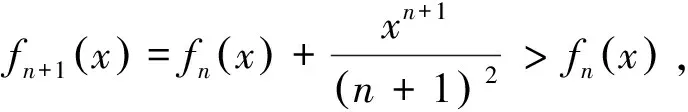
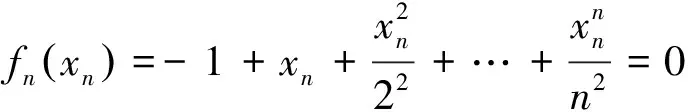
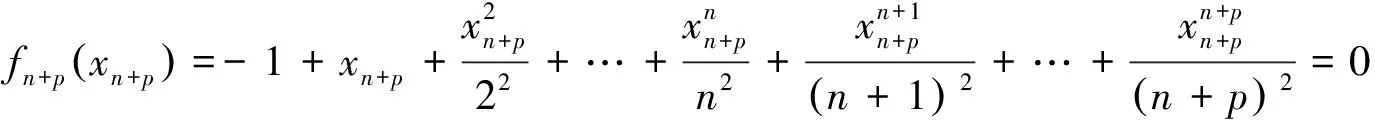
5 结语
