高中数学中常见“齐次结构”的处理办法

江苏省苏州市实验中学 (邮编：215011)

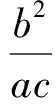
高中数学里有关齐次式的问题经常出现在不等式、三角函数、解三角形、圆锥曲线等章节里，往往需要我们解决一些化简、求值域、最值等问题.

以下我们来分类研究：

1 不等式中的齐次结构

例1已知不等式xy≤ax2+2y2,若对任意x∈[1,2]及y∈[2,3]该不等式恒成立，则实数a的取值范围是________.

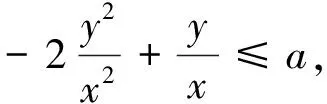
提炼本例中利用齐次结构将不等式中的两个变量x、y合并成了一个变量t！不是齐次式做不到这一点.这是我们在不等式中研究齐次式的重要心得.

当我们对不等式中的齐次特征有了一定的认识后，再来分析下面这道高考题，是不是对其中的一般性规律有更深的理解呢？

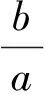
分析条件5c-3a≤b≤4c-a，clnb≥a+clnc为典型的齐次结构.可化为：

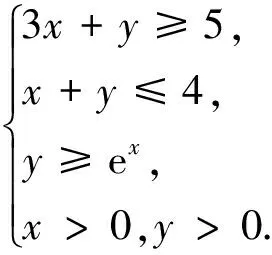
2 三角函数中的齐次结构

例3已知sinα+2cosα=0,求：

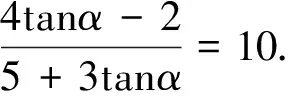
3 解三角形中的齐次结构

分析本题条件3acosC=2ccosA中等号两端a、c为齐次结构，故由正弦定理得a=2RsinA,c=2RsinC,3sinAcosC=2sinCcosA，从而3tanA=2tanC.

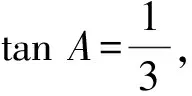
这类题目中如果表示边长的字母是齐次的，则可由正弦定理将边长转换为角的正弦；当三角形中角的正弦齐次时也可以转换为边长.如下例：

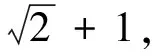
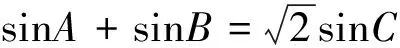
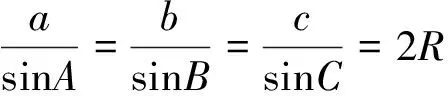
4 圆锥曲线问题中的齐次结构

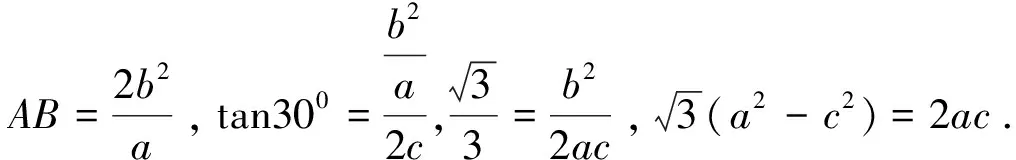
这里就形成了关于a、c的齐次结构!

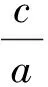
下面我们再来研究一道利用通过齐次结构求椭圆离心率取值范围的例子:

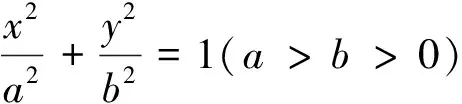
分析先将向量坐标化，设M(x0，y0)，则

①

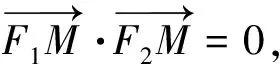
故(x0+c,y0)·(x0-c,y0)=0

②

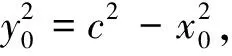
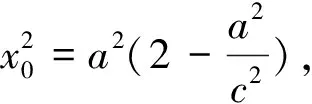
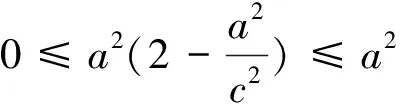
将不等式两端同除以a4可解得：

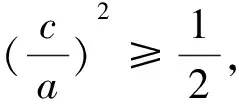
以上是我们在高中数学学习过程中经常遇到的四种类型的含有“齐次结构”的问题，表面看起来它们形式各异并无什么关联，而实际上可以用“齐次”这个词来描述它们共同特征.抓住这个特征就基本掌握了这四种“齐次”问题的一般性方法.