2014年安徽省初中毕业学业考试数学学科试卷分析——基于舒城县考区随机抽样300份数学成绩的统计分析

安徽省舒城县阙店中学 (邮编：231363)

安徽省舒城县教研室 陈先荣 (邮编：231360)

2014年安徽省中考数学试题，保持前两年平稳的特点，充分体现了安徽省“以稳为主，稳中求变”的命题指导思想.命题既重视基础知识与基本技能的考查，又重视与学生生活实际的结合，立足于公平、公正的试题背景，基本没有偏、难、繁、琐的题目，对我省的初中数学教学和其它省市的命题起到了正导向作用，是一份值得肯定的试卷.

1 试卷结构和难度较前两年有所变化

试卷没有超出《安徽省2014年中考(数学)纲要》的要求，试题设置有一定的梯度和灵活度，较2013年难度有所增加，尤其几何题对学生的思维水平较前四年要求提高.整张试卷中“数与代数”77分约占51.3%，“几何与图形”57分约占38%，“统计与概率”16分约占10.7%.均接近于前几年中考各部分所占比例的平均值.

试卷对于一些知识点的考查方式和分值较前两年有所变化，比如：对于圆的考查以往一般以选择或填空题呈现，今年将圆与三角形结合起来，以10分的解答题出现，综合性较以往有所提高;统计问题前几年一直作为解答题，占据10或12分的分值，今年把统计以选择题的形式进行简单的考查，把概率作为12分的问题进行考查，且不仅考查了学生联系实际的想象能力，而且题目摒弃常规的解答和思考方式，具有一定的新颖性.

2 试卷总体情况

2.1 2014年安徽省中考数学试卷的总体情况(安徽中考舒城考区的随机抽样数据分析)

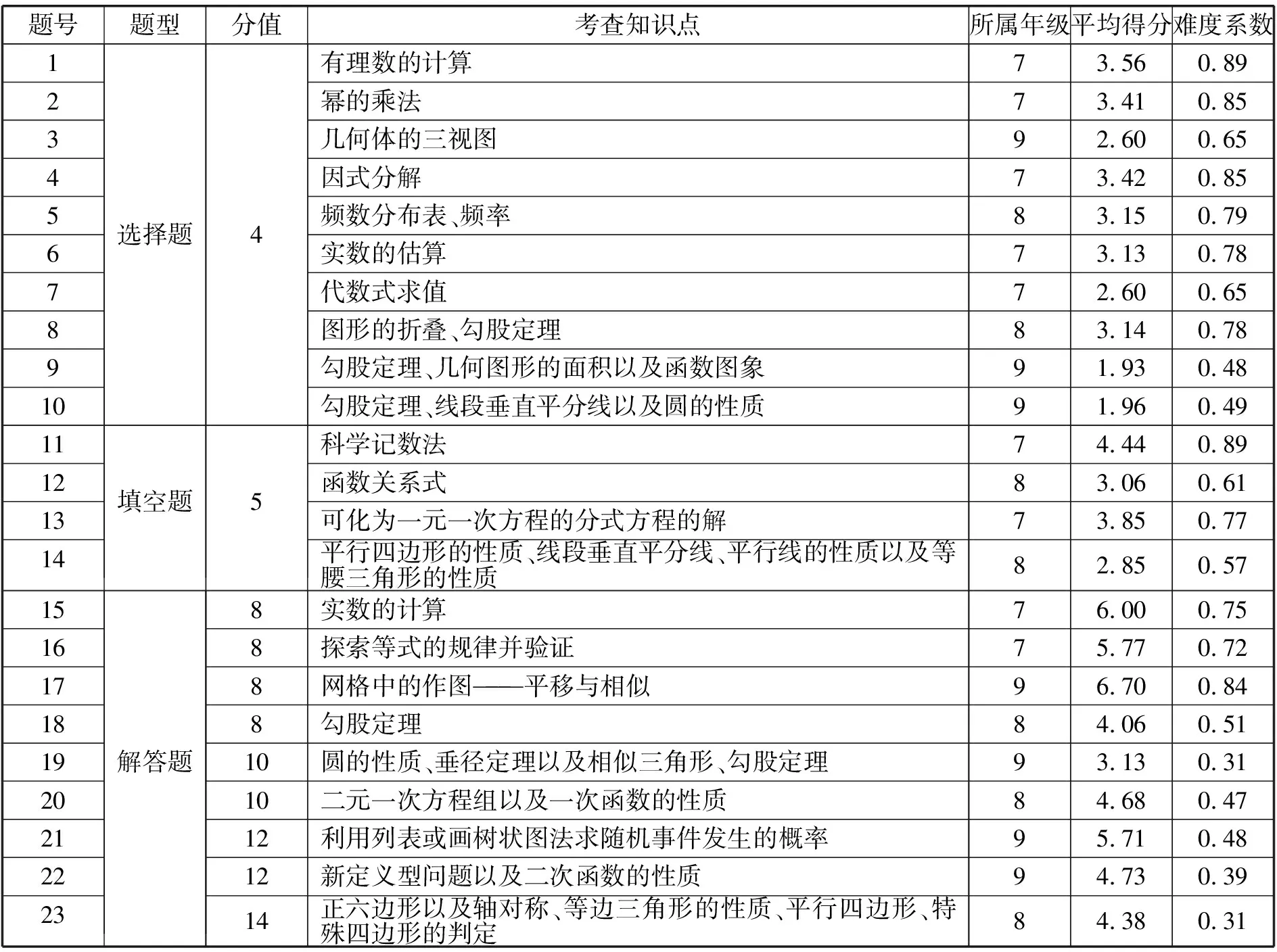
题号题型分值考查知识点所属年级平均得分难度系数12345678910选择题4有理数的计算73.560.89幂的乘法73.410.85几何体的三视图92.600.65因式分解73.420.85频数分布表、频率83.150.79实数的估算73.130.78代数式求值72.600.65图形的折叠、勾股定理83.140.78勾股定理、几何图形的面积以及函数图象91.930.48勾股定理、线段垂直平分线以及圆的性质91.960.4911121314填空题5科学记数法74.440.89函数关系式83.060.61可化为一元一次方程的分式方程的解73.850.77平行四边形的性质、线段垂直平分线、平行线的性质以及等腰三角形的性质82.850.57151617181920212223解答题8实数的计算76.000.758探索等式的规律并验证75.770.728网格中的作图———平移与相似96.700.848勾股定理84.060.5110圆的性质、垂径定理以及相似三角形、勾股定理93.130.3110二元一次方程组以及一次函数的性质84.680.4712利用列表或画树状图法求随机事件发生的概率95.710.4812新定义型问题以及二次函数的性质94.730.3914正六边形以及轴对称、等边三角形的性质、平行四边形、特殊四边形的判定84.380.31

根据上表可得，在随机抽取的300名考生中，数学最高分为148分，最低分为8分.140分(含140分)14人；130—140之间31人；120—130之间38人；100—120之间61人；90—100分之间31人；及格人数76人.2014年安徽中考数学试卷舒城县学生平均得分约为87.79分，总体难度系数约为0.59，试卷较难.客观题和解答题均由易到难排列，梯度比较明显，尤其是最后几道解答题难度过大.

2.2 考卷中所涉及到的各年级的分数统计如下图

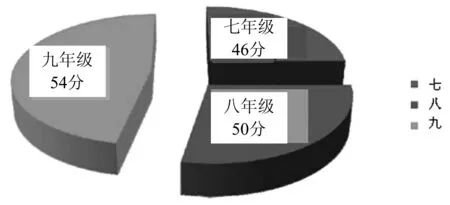
图1 各年级知识点涉及分数

由上图可以看出，九年级知识点涉及分数54分，约占总体的36%；八年级知识点涉及分数50分，约占33%；七年级知识涉及分数46分，约占31%.

2.3 2014与2013考题难易度的对比表

分值类别年份 容易题中档题难题分值得分率分值得分率分值得分率20135436%6946%2718%20145033%5235%4832%

通过上表对比可知：2014年安徽省的中考题比2013年的要难些.可2014年的基础题、中档题易于得分，命题难度系数较往年有所上升，考查的知识点也有创新.

3 试题的分析与点评

2014年安徽省中考数学试题考查内容依据《考纲》，并与2011版《义务教育教育课程标准》修订稿接轨，坚持面向全体，体现“四基”，问题贴近现实生活，题目背景新颖，不仅注重对学生数学素养的检测，还把数学思想方法渗透在考题中.

3.1 突出基础

2014年试题难度在总体上略高于去年，体现了中考试卷的选拔功能.试卷中对于实数的运算、网格作图、二元一次方程组模型的应用都比较基础，对于大多数学生来说，没有思维障碍.全卷中基础题有1、2、3、4、5、6、7、11、12、13、15、17、20等.对于难题的设置也是有梯度的，都分别设置了几个小问题，由易到难，有利于学生分步入手去做，使不同层次的学生都能发挥自己的水平.如第21、22、23题.

例1(第1题) (-2)×3的结果是( )

A.-5 B.1 C.-6 D.6

例2(第2题)x2·x3=( )

A.x5B.x6C.x8D.x9

例3(第3题) 如图，图中的几何体是圆柱沿竖直方向切掉一半后得到的，则该几何体的俯视图是( )

例4(第4题) 下列四个多项式中，能因式分解的是( )

A.a2+1 B.a2—6a+9

C.x2+5yD.x2—5y

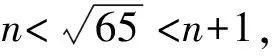
A.5 B.6 C.7 D.8

点评上述5个题目分别涉及到有理数的乘法、幂的乘法、几何体的三视图、多项式的因式分解、实数的估算等简单的题目，这样设置，有利于营造良好的考试氛围，有利于学生在快速、正确地求解后，能以快乐的心情来解答后面问题.

3.2 注重数学思想方法的考查，体现数学本质

数学知识的灵魂是数学思想.今年试卷第7题考查了学生利用整体思想巧妙解决问题，第13题考查了转化思想，第17题，、第18题，第23题有不同程度的画图要求，重点考查了数形结合以及转化等基本数学思想，突显数学本质.

例6(第7题) 已知x2—2x—3=0，则2x2—4x的值为( )

A.—6 B.6 C.—2或6 D.—2或30

点评本题是整体思想的应用.将已知式进行移项，得x2-2x=3，把“x2-2x”看做一个整体直接代入到所求式“2x2-4x=2(x2-2x)”即可.

点评本题考查了转化思想的运用，求解例7时，把分式方程转化为整式方程.

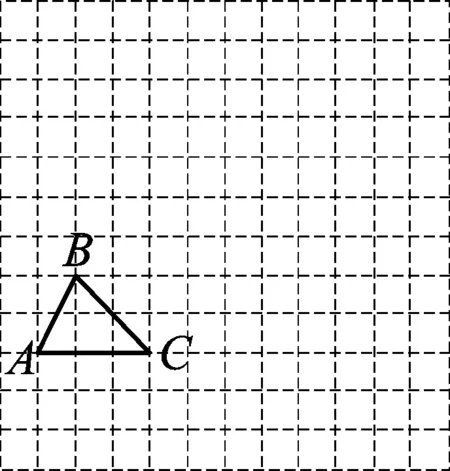
例8(第17题) 如图，在边长为1个单位长度的小正方形组成的网格中，给出了格点△ABC(顶点是网格线的交点).

(1)将△ABC向上平移3个单位得到△A1B1C1，请画出△A1B1C1；

(2)请画一个格点

△A2B2C2，使△A2B2C2∽△ABC，且相似比不为1.

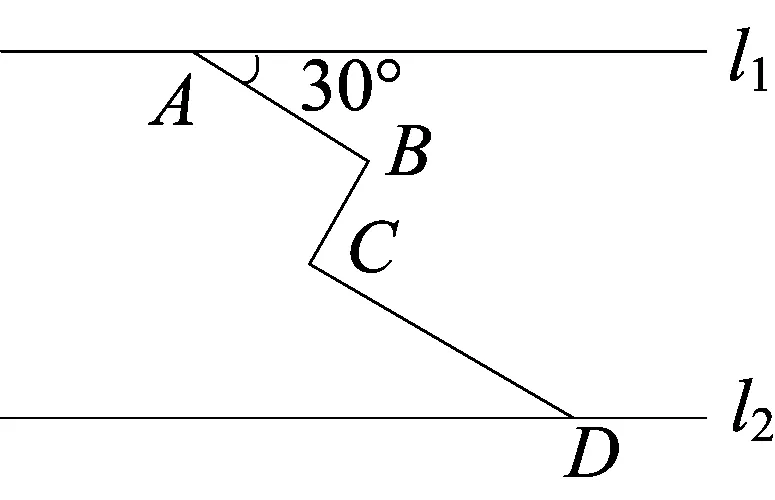
例9(第18题) 如图，在同一平面内，两行平行高速公路l1和l2间有一条“z”型道路连通，其中AB段与高速公路l1成300，长为20km，BC段与AB.CD段都垂直，长为10km；CD段长为30km，求两高速公路间的距离(结果保留根号)

图1

例10(第23题) 如图1，正六边形ABCDEF的边长为a，P是BC边上一动点，过P作PM∥AB交AF于M，作PN∥CD交DE于N，

(1) ①∠MPN

=________；

②求证：PM+PN=3a.

(2)如图2，点O是AD的中点，连接OM.ON.求证：OM=ON.

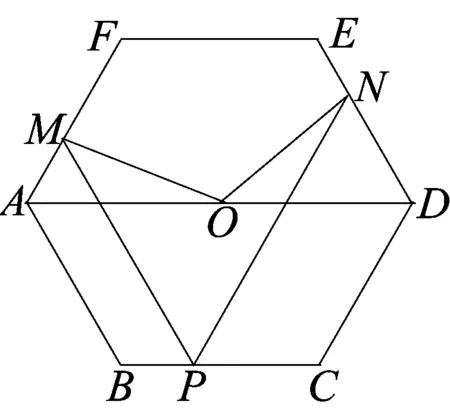
图2

(3)如图3，点O是AD的中点，OG平分∠MON，判断四边形OMGN是否为特殊四边形，并说明理由.

图3

点评例8考查了学生对图形的平移和相似知识的理解以及动手画图操作的能力，注意解答此题关键需要确定三角形顶点变换后的对应顶点. 例9是通过作辅助线将所要解决的问题转化为直角三角形问题进行求解.例10是一道综合性试题，主要考查了正六边形性质，三角形全等判定，等边三角形性质以及菱形的判定等有关知识．解决问题的关键是通过添加辅助线，转化问题．

4 命题启示.

4.1 立足课标，注重“四基”.试题难易分布尊重学生的客观实际，关注学生应试紧张心理及认知水平，在选择、填空题中控制难度，不设置人为障碍，甚至有些题目，在原有的基础上适当增设条件和提供精确的图形，降低学生演绎推理的难度，增加数学活动经验和合情推理能力的考查，从不同角度寻求解决问题的方法.试卷基础题简单明了，只要学生掌握基础的知识点即可解决.如：1、2、3、4、5、6、7、8、11、12、13、15、17、18、19、20、21(1)、22(1)，一般学生可以轻松解答.

4.2 试题清新，贴近教材.试卷的选择与设计大多数是来源于课本的习题或改造题以及2014安徽考纲的变式，对考生具有相当的亲和度.

4.3 关注学生思考方法的培养，提高学生思维水平.今年试卷的第9、10、14、16、18、22、23题都对学生的思维广度和思维深度有一定的要求，所以平常在练习过程中一定要关注思考方法，切忌缺乏思考只追求答案的题海练习.

4.4 关注学生阅读能力的培养.虽然今年对学生阅读题目的要求较以往有所降低，但新定义型问题要引起我们的重视.如今年的第22题以分值12分的解答题，所提供的是最新的背景材料需要学生阅读并掌握新定义“同簇二次函数”，即学即做.公平公正.

4.5 尊重差异，突出选拔.试卷充分照顾了学生的个体差异，根据不同学业水平的学生精心设计了不同层次的题目.尤其是试卷采用双题压轴的形式，试卷最后两题入手不难，第一问很基础，第二、第三问的解答需要一定的综合探究能力.对学生综合思考、解决问题的策略要求较高.有助于考查学生的数学思考以及探究创新能力，同时又具有一定的区分度，符合中考试题具有选拔功能的要求.

4.6 反对“题海战术”，倡导培养学生数学综合素养，一直是这几年中考数学试卷传达的理念，今年的试卷延续了这一理念.呼唤教师转变教学观念，致力于课本资源开发，培养学生数学思维能力，而非机械地增加学生的作业负担.试卷考查内容具有较高的覆盖面和代表性，注重数学“四基”的考查，关注初中数学基本知识与技能、必要的数学活动经验，突出考查化归与转化、函数与方程、数形结合、分类讨论、整体换元等主要数学思想方法，强化技能训练，提高解题能力.