2014年高考数学(理科)数列试题分析及教学建议
2014-08-22合肥工业大学附中邮编230009
合肥工业大学附中 (邮编:230009)
1 2014年全国高考(理科)试题数列部分的统计分析
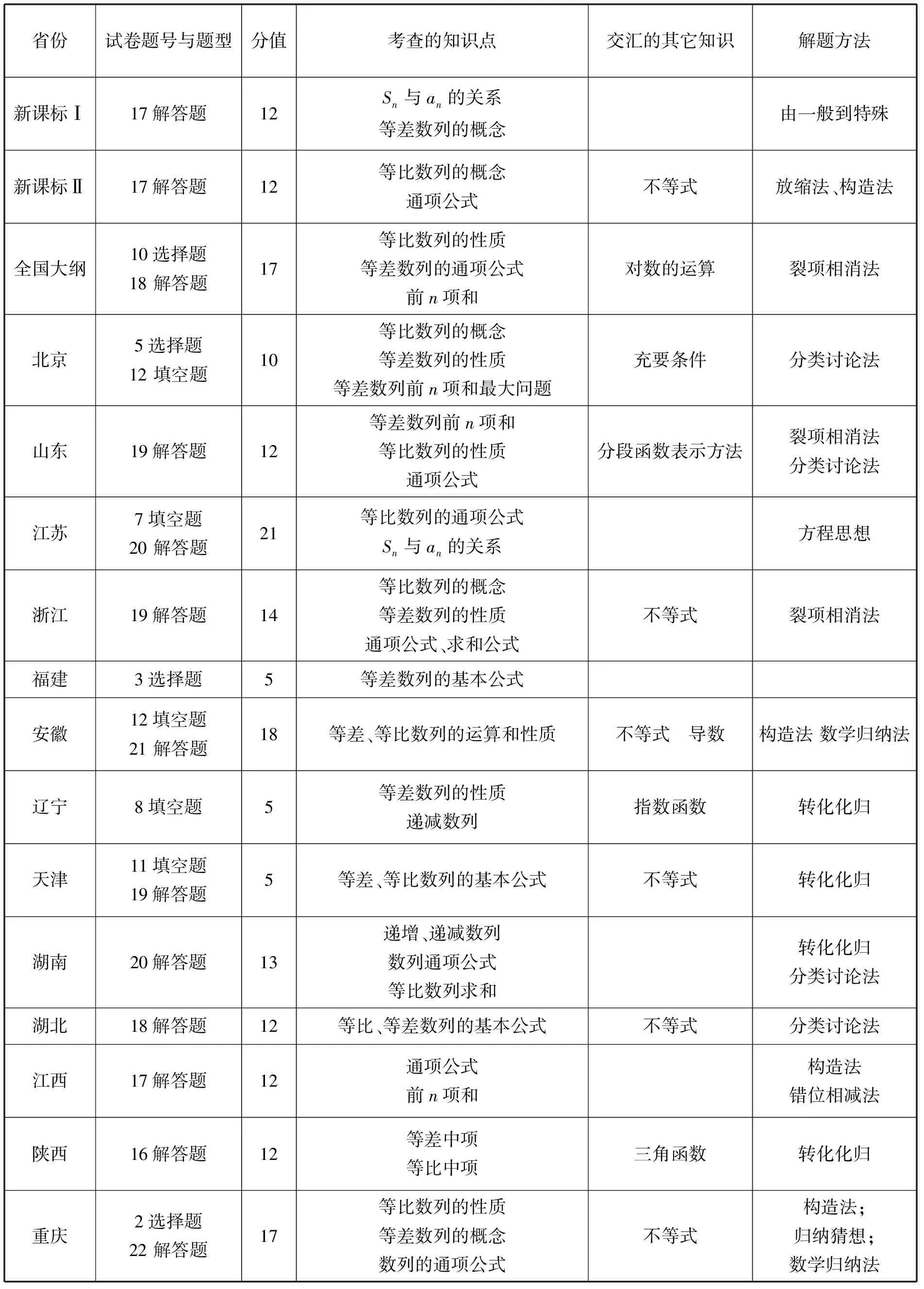
表1 2014年全国高考(理科)试卷数列试题分析
从上表中可以看出,数列作为高中数学的主干知识,在2014年全国高考各省试题中均有考查.
从分值分布上分析,福建以1道选择题呈现,辽宁以一道填空题呈现,分值均为5分;北京卷同时以1道选择题、1道填空题出现,分值共计10分;其他省份均在分值较高的解答题中考查数列问题,分值在12分到21分不等.
从试题出现位置上看,数列考点的解答题多出现在解答题型的前2道,以考查基本知识、数学运算能力为主.同时,数列试题与其他知识点综合,出现在部分省份的高考解答题的中间偏后甚至压轴题位置,以全面考查学生的综合思维能力.
从考查的知识点的角度,统计分析数列考点相关高考试题,考查的知识点中,有11份试卷考查数列的综合应用.试题形式中,出现次数最多的解答题基本上都是设置两小问形式,求通项公式和前n项或者证明等差等比数列相关的不等式.
从试题难度设置上,所有试题都属于常规题,尤其是以选择题填空题形式出现的数列题,都是用解决数列问题的通性通法可以解决的问题.除此以外,数列题还被放置到了压轴位置,对学生能力要求较高.
2 高考数列问题典型考题分析
2.1 填空选择题
今年高考理科试题中有9个省份以选择填空题形式考查了数列问题.全部都是考查等差等比数列的基本公式和性质等基础知识,考查考生的运算能力,总体难度中等偏低.
例1(安徽卷12题) 数列{an}是等差数列,若a1+1,a3+3,a5+5构成公比为q的等比数列,则q=________.
评析本题考查等差等比数列基本运算和性质.从基本量计算的角度看,可以列方程求解,这是通法,有一定的运算量;从性质的角度看,数列a1,a3,a5成等差数列,数列1,3,5也成等差数列,故a1+1,a3+3,a5+5仍然成等差数列,又a1+1,a3+3,a5+5构成公比为q的等比数列,故q=1.此法无计算量.体现了“多考想的,少考算的”的命题理念,体现了思维的灵活性.
例2(全国大纲卷10题) 等比数列{an}中,a4=2,a5=5,则数列{lgan}的前8项和等于( )
A.6 B.5 C.4 D.3
评析本题考查等比数列性质和对数运算,但不同的角度,可以展现不同的思维能力层次.
解法1求通项,再求和.(解略)
解法2利用性质求{an}的前8项积,再求数列{lgan}的前8项和.
a1a2…a7a8=(a4a5)4=104,故lga1+lga2+…+lga7+lga8=4.
解法3{an}成等比数列,则数列{lgan}成等差数列,
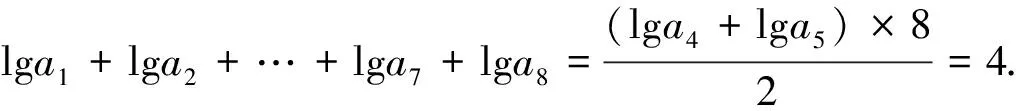
填空选择题型一般均为考查学生的基本知识、基本方法、基本能力.针对数列问题,需要理解等差、等比数列的定义,熟练掌握通项公式、求和公式的灵活运用.此部分试题应属于考生的基本拿分题,力求准确、快捷.
2.2 基础解答题
今年理科试卷中有9个省份数列解答题放置在解答题靠前位置,难度较低.有8个省份数列试题第一问都是求数列的通项公式,其中已知是等差等比数列用基本量法求解的占多数,其次是用构造法求数列通项公式以及利用an和Sn关系求解的;除求解通项公式外,有7个省份是求数列前n项和,重点考查等差等比数列求和以及用错位相减法,裂项相消法等常用数列求和方法.
例3(全国大纲卷第18题) 等差数列{an}的前n项和为Sn,已知a1=10,a2为整数,且Sn≤S4.(I)求{an}的通项公式;
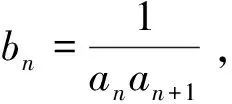
评析本题考查了首项为正,公差为负数的等差数列前n项和的最大问题.另外,本题还考查了裂项相消法求数列前n项和.山东卷和浙江卷也考查了该方法.
此类试题需要考生在掌握数列知识点的基本内容基础上,熟悉各种解题思路与方法,如裂项相消法、错位相减法等,能熟练运用各类数学方法解决数学问题.
2.3 数列综合题
高考数列试题除了以选择填空题、基本解答题等形式出现,重点考查学生对数列问题的基本性质、基本公式的理解和掌握外,还因数列问题本身的灵活性、较复杂的运算要求,往往与其他知识点交汇组合,成为高考试题的压轴综合题.
例4(天津卷 第19题) 已知q和n均为给定的大于1的自然数.设集合M={0,1,2,…,q-1},集合A={x|x=x1+x2q+…+xnqn-1,xi∈Mi,i=1,2,…,n}.
(Ⅰ)当q=2,n=3时,用列举法表示集合A;
(Ⅱ)设s,t∈A,s=a1+a2q+…+anqn-1,t=b1+b2q+…+bnqn-1,其中ai,bi∈M,i=1,2,…,n. 证明:若an 评析本题主要考查集合的含义和表示,等比数列的前n项和公式,不等式的证明等基础知识和基本方法. 考查运算能力、分析问题和解决问题的能力. (1)若b=1,求a2,a3及数列{an}的通项公式; (2)若b=-1,问:是否存在实数c使得a2n 评析(Ⅰ)解法1构造等差数列{(an-1)2} ; 下面用数学归纳法证明加强命题:a2n 先证0≤an≤1(n∈N*) ①(略) 再证a2n ②(略) 又由①、②及f(x)在(-∞,1]上为减函数得f(a2n)>f(a2n+1),即a2n+1>a2n+2, 本题是重庆卷的压轴题,难度较大.无独有偶,安徽卷第21题也是有关数列的压轴题.不难发现它们的相似之处,均以数列为载体,考查了证明不等式的两种方法:数学归纳法、利用导数证明函数的单调性进而得到不等关系.可见数列与不等式结合考查的题型我们需要多训练. 例6(江苏卷) 设数列{an}的前n项和为Sn.若对任意的正整数n,总存在正整数m,使得Sn=am,则称{an}是“H数列”. (1)若数列{an}的前n项和Sn=2n(n∈N*),证明:{an}是“H数列”; (2)设{an}是等差数列,其首项a1=1,公差d<0.若{an}是“H数列”,求d的值; (3)证明:对任意的等差数列{an},总存在两个“H数列”{bn}和{cn},使得an=bn+cn(n∈N*)成立. 评析本题“H数列’属于新概念型问题,题目新颖,要求学生具备较好的自学探究能力.主要考查数列的概念、an与Sn的关系,等差数列等基础知识,以及学生的推理论证能力. 由以上的分析可以看出,对数列知识的考查,基本是“一小一大”.小题注重数列的通项公式,等差等比数列的性质与基本量的求解.大题以等差等比数列知识的综合运用为主,或结合其它知识(一般是函数、不等式)与数学归纳法,考查考生综合运用知识分析问题、解决问题的能力、推理论证能力.具体到数列知识的复习备考,需要注意以下几点: (1)对数列通项公式的探求是高考考查数列的一个主要命题点,可以考查考生的观察、分析、归纳、猜想、推理论证能力.因而熟练求通项公式的常用方法:如用方程思想利用基本量解决等比等差数列通项公式;构造等差等比数列进而求解数列的通项公式;归纳猜想求数列通项公式;利用前n项和公式求通项公式;特别是由递推关系确定通项公式,变化多,较灵活等. (2)等差等比数列是数列中研究的重要内容.熟练掌握等差等比数列的定义、通项公式、求和公式和性质,是解决数列综合问题的基础,许多数列问题,都可以转化为等差等比数列来解决,如利用放缩法将一般数列转化为等差等比数列问题进而证明不等式. (3) 数列求和一般与不等式证明相结合,因而需熟练求数列前n项和的方法,如对于等差等比数列用公式法;错位相减法,裂项相消法,分组求和法、倒序相加等等. (4) 从函数的角度理解数列是必要的,这样就可以利用函数的思想与方法来处理数列问题.在数列不等关系的问题中,通过把数列问题转换为函数问题,利用函数的工具,解决数列问题是很常用的手段.但要注意函数的单调性与数列的单调性还是有区别的,解题时要关注和体会它的不同. (5) 厘清知识间的交汇点,注重多个知识点的综合题的训练与解题方法的积累.如数列与三角函数结合、数列与集合结合,数列与导数结合,数列与解析几何结合、数列与平面向量结合、数列与不等式结合等问题.特别是数列与函数、不等式结合问题,它综合了函数性质、导数、数列、不等式、数学归纳法等方面的知识与方法,对考生综合运用知识分析问题、解决问题的能力有较高的要求,对高分学生有很好的区分度,因而以数列为背景的不等式的证明问题以及以函数为背景构造数列的问题,成了高考压轴题的宠儿. (6)注意强化运算能力训练.从以上例题可以看出数列题计算量相对较大,能不能熟练准确的计算直接影响答题的速度和准确率.因此,在复习时必须重视训练对数式运算能力的提高.
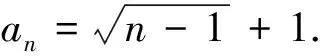
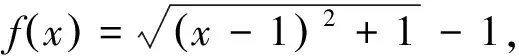
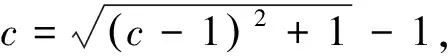
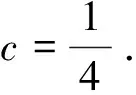
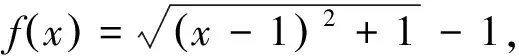
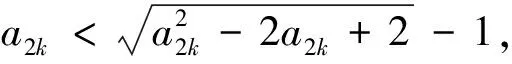
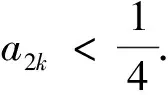
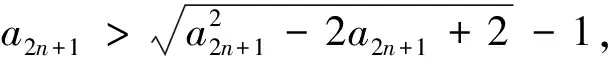

2.4 新概念型数列问题
3 对高三数列复习的建议
