对一类高考题目的研究
2014-08-22山东省宁阳一中邮编271400
山东省宁阳一中 (邮编:271400)

1 函数的性质应用

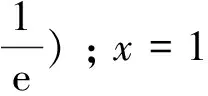
例1(2014年天津卷理20)已知函数f(x)=x-aex(a∈R),x∈R.已知函数y=f(x)有两个零点x1、x2,且x1 (Ⅰ)求a的取值范围; (Ⅲ)证明:x1+x2随着a的减小而增大. (Ⅲ)证明略. (Ⅰ)当k≤0时,求函数f(x)的单调区间; (Ⅱ)若函数f(x)在(0,2)内存在两个极值点,求k的取值范围. 解(Ⅰ)略; 例3(基于函数性质的原创题目)已知函数 (1)若x>0时,f(x)>g(x)恒成立,求a的取值范围; (2)讨论f(x)-g(x)=0零点的个数. 例4(2014年湖北卷理22)π为圆周率,e=2.71828…为自然对数的底数. (Ⅱ)求e3,3e,eπ,πe,3π,π3这6个数中的最大数与最小数. (Ⅲ)将e3,3e,eπ,πe,3π,π3这6个数按从小到大的顺序排列,并证明你的结论. 当0 故只需比较e3与πe和eπ与π3的大小. ① 综上可得,3e (1)若h(x)=f(x)+g(x)在(1,+∞)内为减函数,求实数a的取值范围; (2)若存在x1、x2∈(1,e2],使得f(x1)≤f′(x2)-g′(x2)成立,求实数a的取值范围. 解所以因为x∈(1,+∞),所以lnx∈(0,+∞),则(0,∞),所以时,故 (2)“存在x1、x2∈(1,e2],使得f(x1)≤f′(x2)-g′(x2)成立”等价于“x1、x2∈(1,e2]时,f(x1)min≤(f′(x2)-g′(x2))max”. 设u(x)=f′(x)-因为x∈(1,e2],所以∞),当时,即所以故 (Ⅰ)求a、b; (Ⅱ)证明:f(x)>1. (Ⅰ)解函数f(x)的定义域为(0,+∞), 由题意可得f(1)=2,f′(1)=e. 故a=1,b=2. 综上,当x>0时,g(x)>h(x),即f(x)>1. 同一个地区的历年高考题目一般都保持了连续性、稳定性的特点,所以通过研究高考题目,我们积极地加以分析,进行举一反三的拓展,在增强高考预测能力的同时,还可使学生跳出题海,对提高高考应试能力大有裨益。






2 函数的性质应用





3 函数y=xex的性质应用



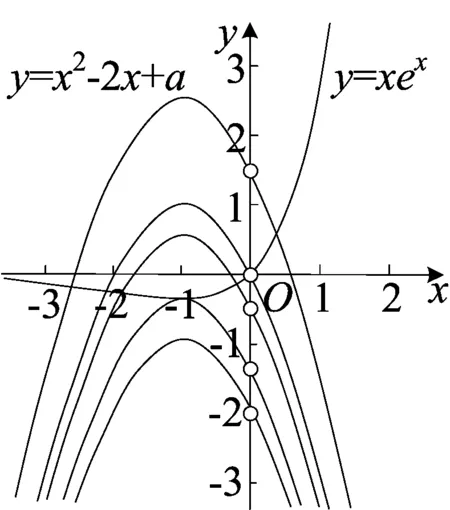





4 函数的性质应用








5 函数的性质应用




6 函数y=xlnx的性质的应用




