抓住不变量 优化解题过程

安徽省合肥市第一中学 (邮编：230601)

很多数学问题中，虽然数量、图形在发生变化，但其中往往隐含着某些不变量(性).如果能在变化过程中善于发现并挖掘利用这些因素，就常能使解题达到一种意想不到的境界.

1 运用不变量，简化运算过程

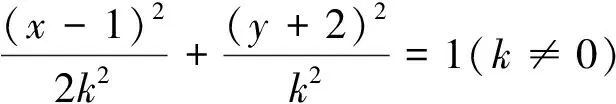
2 挖掘不变量，打开解题的突破口

例3下图是一个3×8的纵横线路图，一只小虫沿纵横线向上或向右从A点爬到B点，则不同的爬行方式的总数是________．

图1

分析解决本题的一种有效方法就是利用面积不变量，即S△MF1F2=S△MF1F2.“算两次”的方法其实就是利用不变量的原理.

解由已知得，a=5，b=4，c=3.

△MF1F2的周长=|F1F2|+|MF1|+|MF2|=2a+2c=16.

又b=4，所以，只有短轴的两个端点符合条件.

例6已知直线m、n及平面α，其中m∥n，那么在平面α内到两条直线m、n距离相等的点的集合可能是：①一条直线，②一个平面，③一个点，④空集.其中正确的序号是________．

分析因为m∥n，所以m、n确定一个平面，记为β，在平面β内作m、n的平行线l，使l到m、n的距离相等，过l作平面γ⊥β，则到直线m、n的距离相等的点的集合为平面γ，这是一个形的不变量.抓住这个不变量，只需考察γ和γ的所有可能的位置关系情况，就可得出正确的序号是①、②、④.

3 寻求不变量，明确探索方向

例7设集合A={(x,y)|xcosθ+ysinθ=1}，全集U={(x,y)|x,y∈R}，求集合A的补集对应的图形是什么？

分析解决问题的关键是发现不变量cos2θ+sin2θ=1.

解法2由柯西不等式得1=12=(xcosθ+ysinθ)2≤(x2+y2)·(cos2θ+sin2θ)，即x2+y2≥1，A={(x,y)|x2+y2≥1}，所以，集合A的补集对应的图形是单位圆x2+y2=1内(不包括圆)的点集.

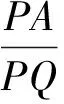
4 构造不变量，另辟解题新径

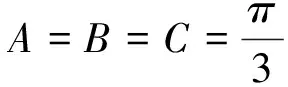
总之，有意识地利用不变量(性)原理解题，可以开阔学生的视野，培养学生思维的灵活性和深刻性，提高学生分析问题、解决问题的能力.

1 陶兆龙.利用不变量(性)解解几题[J].中学数学(苏州),1996(8)

2 李静.不变量原理在数学解题中的运用[J].考试周刊,2010,44

3 王华民,朱国伟.一类解析几何定值问题的求解策略[J].数学教学研究,2013(4)

4 兰诗全.不变量解题四功能[J].上海中学数学,2014(1-2)