2014年高考数学全国课标卷特色小题赏析

河北省武邑县职教中心 (邮编：053400)

我们期待已久的2014年全国高考已悄然落下帷幕，本着承上启下的命题思想及在继承中有发展的命题原则，全国卷为我们呈现了许多优秀的特色小题，以全国课标Ⅰ理科数学的部分选择题和填空题为例，让我们一起回顾赏析一下.

赏析以向量为载体对圆锥曲线知识的考查，历来是高考命题者的最爱.命题者试图让考生借助于数形结合思想，实现了对抛物线的定义的考查，也易于考生解题思路自然流畅地展开.

故选C.

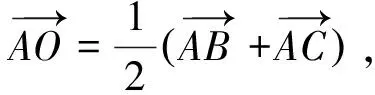
赏析已知条件是一个我们再熟悉不过的结论，但由于命题者为它量身创设了一个特定的环境，便产生了一个特定的结果，带给我们的虽是旧题但很有新意的感觉.其实一个好的题目就是一些简单题目的好的有机组合.由此可见，熟记一些结论对我们解题是大有裨益的.

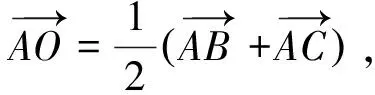
试题三( 第6题) 如图，圆O的半径为1，A是圆上的定点，P是圆上的动点，角x的始边为射线OA，终边为OP，过点P作直线OA的垂线，垂足为M，将点M到直线OP的距离表示为x的函数f(x)，则y=f(x)在[0,π]上的图象大致为( )

试题四(第16题) 已知a,b,c分别为△ABC的三个内角A,B,C的对边，a=2，且(2+b)(sinA-sinB)=(c-b)sinC，则△ABC面积的最大值为________.

赏析此题集中考查了正弦定理、余弦定理、三角形面积公式、均值不等式等多个知识点，是一道具有较高能力要求的综合性试题.本着高考要具有选拔性功能和试题要有梯度的命题原则，所以命题者特意把它作为填空题的压轴题.这是一道考查考生思维能力和计算能力的好题.

解由正弦定理得(a+b)(a-b)=(c-b)c，也即a2=b2+c2-bc.由余弦定理得

所以A=60°.又因为a=2，所以4=b2+c2-bc.又由均值定理得4=b2+c2-bc≥2bc-bc=bc，所以bc≤4，所以

试题五(第14题) 甲、乙、丙三位同学被问到是否去过A、B、C三个城市时，甲说：我去过的城市比乙多，但没去过B城市；乙说：我没去过C城市；丙说：我们三人去过同一个城市.由此可判断乙去过的城市为________.

赏析这是一道反映实际生活场景考查逻辑思维能力的格调清新的小题，印证了“数学来源于生活而高于生活”这一主题.高考的指挥棒也积极引导我们在平时的教学中一定要关注生活，真正使数学的美，体现在实实在在的应用之中，突出数学作为工具的实用性价值.

解可以按照丙、乙、甲的顺序验证排除即可.故填A.

试题六(第9题) 不等式组

p1：∀(x,y)∈D，x+2y≥-2，

p2：∃(x,y)∈D,x+2y≥2，

p3：∀(x,y)∈D,x+2y≤3，

p4：∃(x,y)∈D,x+2y≤-1，

其中真命题是( )

A.p2，p3B.p1，p4C.p1，p2D.p1，p3

赏析不拘泥于常规的求目标函数z=x+2y的最值，含蓄地借助于“存在性”、“任意性”等数学语言，乔装打扮，使得这一小题同时具备了灵活性和开放性等特点，达到了对线性规划问题的考查目的.