一类非线性三阶边值问题正解的存在性①

王晓燕， 张 莉

(兰州工业学院基础学科部，甘肃兰州730050)

0 引言

三阶微分方程在应用数学与物理学等不同的领域有极其重要的应用，例如带有固定或变化横截面的屈曲梁的扰度，三层梁，电磁波，地球引力吹积的涨潮等，见文献［1］.基于这样的实际背景，三阶常微分方程边值问题也就备受学者的广泛关注，见文献［2～6］.特别的，文献［6］运用锥拉伸与锥压缩不动点定理研究了三阶常微分方程边值问题

正解的存在性，其中 λ ＞0是参数，a∈C(［0，1］，［0，∞))，f∈ C(［0，∞)，［0，∞))

然而，在a变号的情形下，对三阶常微分方程边值问题(1)正解的存在性还没有文献讨论过.本文运用Leray－Schauder不动点定理，在a变号的情形下讨论了三阶常微分方程边值问题(1)正解的存在性.

本文总假设:

(H1)λ＞0是正参数;

(H2)f:R+→R连续且f(0)＞0;

(H3)α，β ≥0，α + β ＞ 0.

1 预备知识

引理1.1［6］线性边值问题

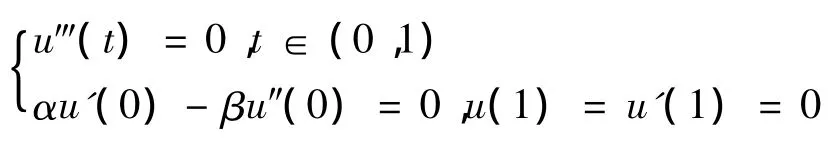
的Green函数为

且具有以下性质:

证明 对 ∀u ∈ C［0，1］，定义算子

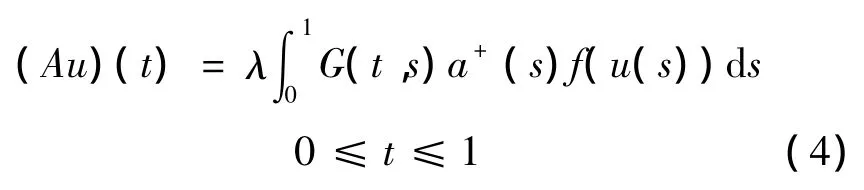
易知 A:C［0，1］→C［0，1］全连续且算子 A的不动点就是问题(3)的解.

取 ε ＞0，使得

设 u ∈ C［0，1］，θ∈ (0，1)，满足 u= θAu，则由(4)以及的非减性可知

或者

(8)结合(6)可得‖u‖≠Aλ.注意到当λ→0时，Aλ→0.由Leray－Schauder不动点定理知，A存在一个不动点满足且

2 主要结果及证明

本文的主要结果如下:

定理2.1 设条件(H1)－(H3)成立，并且(H4)a∈C(［0，1］，R)，a不恒为零，且存在k ＞ 1，使得［0，1］成立，其中a+，a－分别表示a的正部和负部.则存在正数λ*，使得当λ＜λ*时，问题(1)至少存在一个正解.

证明 令.由(H4)，则存在正常数α，γ∈(0，1)，对任意的s∈［0，α］，t∈［0，1］有

固定 δ∈(γ，1)，并设 λ*＞0，对任意的 λ ＜λ*有

成立.

对λ ＜ λ*，假设问题(1)有形如λ+vλ的解记为 uλ，则 vλ满足

对任意的ω∈C［0，1］，定义算子

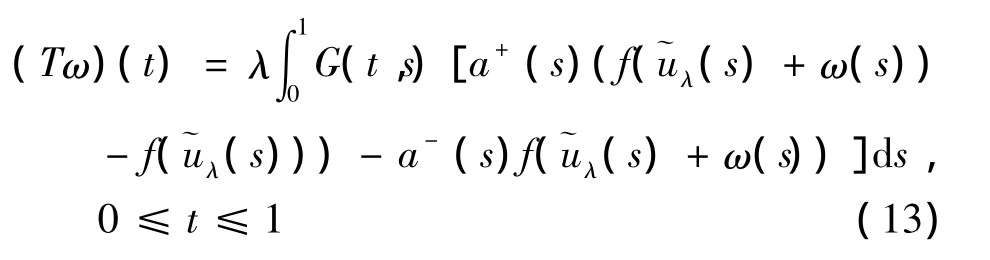
易知 T:C［0，1］→ C［0，1］全连续.

设 v∈ C［0，1］，θ∈ (0，1)满足 v= θTv，则

由于

由(11)知

上式结合(9)，(14)可得

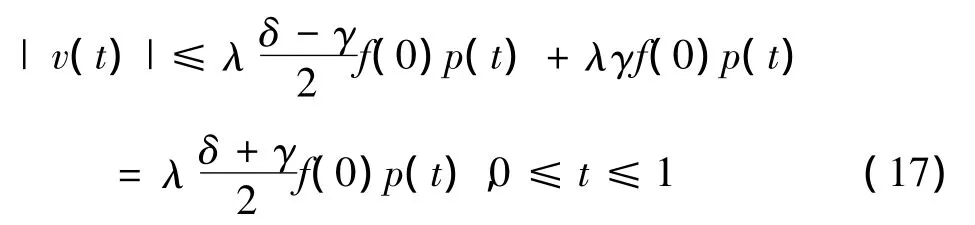
由Leray－Schauder不动点定理知，T有不动点 vλ满足.因 vλ满足(17)，结合引理1.2知

即问题(1)有一个正解uλ.

注:本定理2.1的证明采用了与文献［7］相类似的方法.

［1］M.Gregus，Third Order Linear Differertial Equations，in:Math.Appl.，Reidel，Dordrecht，1987.

［2］R.Ma.Multiplicity Results for a Third Order Boundary Value Problem at Resonance，Nonlinear Anal.，1998，32(4):493 －499.

［3］Z.J.Du，W.G.Ge，X.J.Lin.Existence of Solutions for a Class of Third － Order Nonlinear Boundary Value Problems［J］.Math.Anal.Appl.，2004，294:104 －112.

［4］Y.Feng，S.Liu.Solvabolity of a Third － Order Two － Point Boundary Value Problem［J］.Appl.Math.Lett.，2005，18:1034－1040.

［5］S.Li.Positive Solutions of Nonlinear Singular Third － Order Two－ Point Boundary Value Problem［J］.Math.Anal.Appl.，2006，323:413－425.

［6］Sun H.Wen W.On the Number of Positive Solutions for a Nonlinear Third Order Boundary Value Problem［J］.Int.J.Differ.Equ.，2006，1:165 －176.

［7］D.D.Hai.Positive Solutions to a Class of Elliptic Boundary Value Problems［J］.Math.Anal.Appl.，1998，227:195 －199.

［8］郭大钧.非线性泛函分析［M］.济南:山东科学技术出版社，1985.