车道被占用对城市道路通行能力影响的评估①

胡红飒， 朱家明， 孙 宁， 陈淑雅

(安徽财经大学1.国际经济贸易学院;2.统计与应用数学学院，安徽蚌埠233030)

0 引言

影响道路通行能力的主要因素大体可分为道路条件、交通条件和交通外环境等.道路条件指的是道路几何组成状况，如车道数、车道宽度、路面状况等;交通状况指的是交通流的车辆组成和分布规律特性，如交通量大小、行人、非机动车干扰等;交通外环境指的是道路交通以外的自然条件，如沿线地形、景观、气候等.本文旨在分析道路条件和交通状况两种因素并建立车道被占用对城市道路通行能力影响(详见2013高教社杯全国大学生数学建模竞赛A题).

1 车道被占用对城市道路通行能力的影响建模

(一)交通事故发生至撤离期间，事故所处横断面实际通行能力变化过程的分析.

(1)建模准备

1)数据的获取依据:

通过观察视频对通行车辆的数据进行提取.上游路段的交通流量是由上游路口的交通信号灯所控制，信号灯以一分钟为由绿灯转为红灯的一个周期.为了消除周期的影响，选取一分钟为单位时间统计路段的最大车辆数.上游路口处信号灯在整分钟时点处于绿灯，通过绿灯的车流30秒后到达事故点处，此时路段内的车辆数为最大车辆数，因此将绿灯后30秒的画面定格进行统计.

统计最大车辆数时，以标准车辆(小汽车)为单位，引用表1中的等效通行能力的当量标准［1］.

表1 等效通行能力的当量标准

统计出上游240m路段内道路1，2，3的每分钟的最大车辆数，如表2所示:

表2 上游240m路段内道路1，2，3的每分钟的最大车辆数

其中，第14和16分钟的数据由于视频的原因无法统计出，所以由Matlab进行插值［2］得出.

2)定义1:道路通行能力:道路通行能力是指道路上某一点某一车道或某一断面处，单位时间内可能通过的最大交通实体(车辆或行人)数，均采用等效通行能力的当量标准车辆为单位(pcu).

3)定理:第i分钟车速与车流密度的对数模型为vi=vm×ln(kj/ki)

其中，vm为最佳交通流速度(取30公里/h);kj为v=0时的交通流密度，称阻塞密度(取600辆/km).

(2)模型的建立与求解

1)基本通行能力

通行能力按具有标准长度的车辆，以前后两车最小车头间隔连续行驶时，单位间内通过第m道路上指定断面的最大车辆数记作nm(辆 /h):

其中，在一般情况下可取司机刹车的反应时间t0=1s，系数 c=0.01，安全距离 d3=2m，小型车辆的标准长度d4=5m［3］.将vi带入(1)式可以得到每条道路的基本通行能力［4］.

2)实际通行能力

道路的通行能力不仅受交通状况的影响，还受路况的影响［5］.根据折减系数的标准［6］，当道路为多车道时，靠近中心线的第二车道的折减系数为1;靠近缘石的车道通行能力最小，即第一、三车道的折减系数为0.85.当车道的宽度小于必需的3.5m 时，折减系数 α2为 0.94［6］.由此可以得到路段的实际通行能力为:

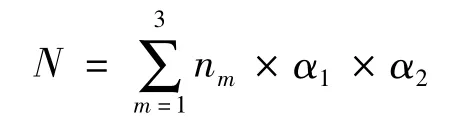
由每分钟车辆数，利用定理可得三条道路的交通速度.将交通速度带入式(1)，可得三条道路各自的通行能力，加总得道路通行能力如表3所示.

表3 道路通行能力(pcu/h)

为了直观的观察道路的实际通行能力的变化趋势，绘制实际道路通行能力的折线图如图1所示.

图1 道路通行能力变化图

由图1可知道路通行能力的变化过程很平缓，在交通事故刚发生时，道路的通行能力有所下降;随后道路的通行能力不断加大;随着交通时间的持续，在最后阶段交通能力呈下降趋势.

(二)估算从事故发生开始经过多长时间车辆排队长度将到达上游路口

(1)建模准备

首先根据给定的路段上游车流量，换算出每个周期的车流量;其次在合理的假设条件下算出每个信号周期从上游路段驶出的车辆数及单位时间内发生事故路段净增加的车辆数;最后用排到路口时的总车辆数和单位时间内净增加的车辆数，根据红绿灯不同情况的汽车流量讨论最终到达上游路口用的时间.

1)模型的假设:

①设进入事故路段的车载路段中做匀减速运动，汽车到达事故发生点的速度为0;

②假设发生交通事故时上游路口刚好发生信号灯转换;

③汽车刚进入事故发生路段的速度为30km/h，每辆车从进入事故发生路段到离开事故发生路段用时30s.

2)选取合适参数

由下游方向需求不变，可知必须有汽车通过上游，即汽车从上游路口减速行驶到事故发生点的速度不为零，才可以进入下游.设汽车不能通过上游路段进入下游路段的临界制动加速度为am/s2，求解得出最大制动加速度a=0.145m/s2，汽车能够顺利通过时实际的制动加速度a应小于0.145m/s2，现取为 a=0.143m/s2.

(2)模型的建立与求解

1)进入事故发生路段的车流量会随着信号灯的改变而变化(图2和图3标出了事故发生点).

图2 交通事故示意图

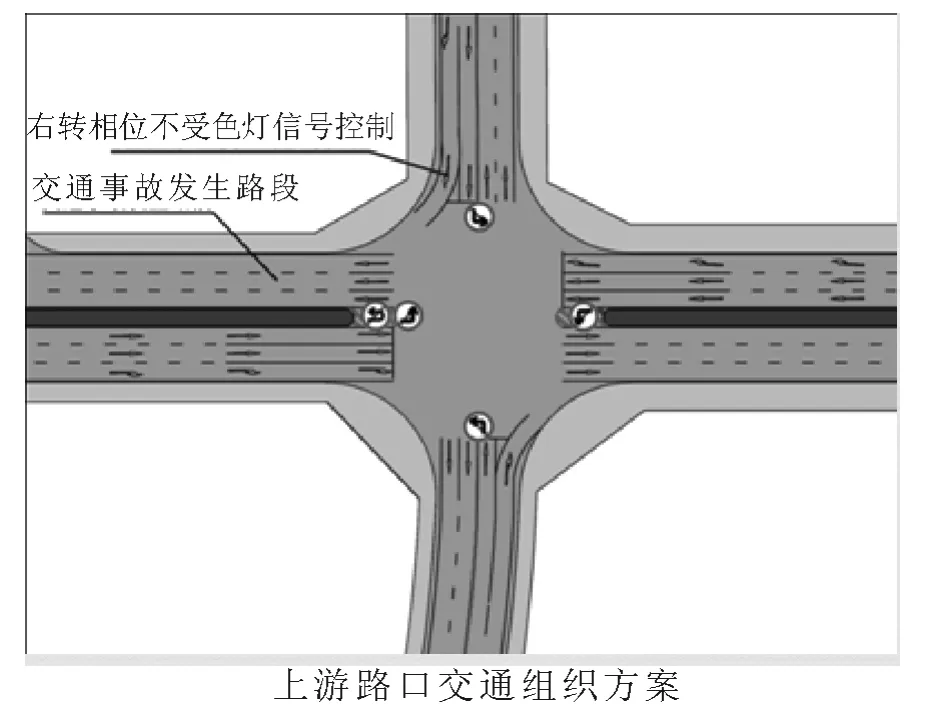
图3 视频1中交通事故位置示意图

第一相位时，右转路口不受信号灯控制，此段时间事故发生路段的流量是上游路口右转流量和直行流量之和，且与总流量的比为p1;第二相位时，此段时间内事故发生路段的车流量仅为上游路口右转的车流量，且与总流量的比为p2.由图3得到在路口正常通行时车辆流量来源方向见表4.

表4 车辆流量来源

每分钟不同相位发生时的车流量为:

其中，M是上游路段每分钟的车流总量(pcu)，(p1+p2=1).

第一相位时，p1为0.76，代入(2)得到 q1=19;第二相位时，p2为0.24，代入(3)式有 q2=6.

2)设 t时刻的排队车辆为 y(t)，在［t，t+dt］时间段内，单位时间(每分)内有m辆汽车驶出上游路段，有M辆汽车驶进上游路段，由题意可知初始排队辆为0，建立微分方程［7］:

每分钟的车流量是由两种相位控制的，在y不能被M－m整除的情况下，要考虑信号灯对流量的控制来估算总时间，有:

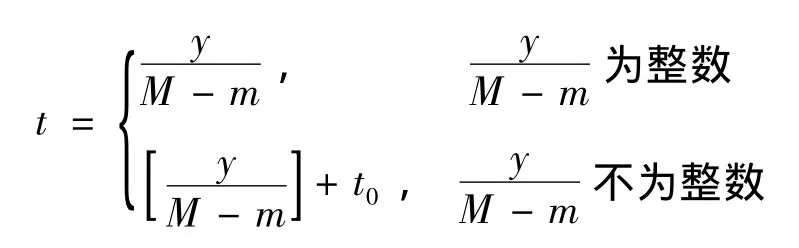
在事故未被处理期间的［t，t+d t］时间段内，由于每次只能通行一辆，故每分钟可以离开事故发生路段的车辆数为2辆.每分钟有25辆汽车驶进上游路段(路段上游车流量为25pcu/min)，所以每周期净流进上游路段的车辆数(M－m)=23.

当车辆排队到达上游路口时，上游路段140米可容纳84辆长度为5米的标准车辆.排除出事故的两辆车，所以排队的车辆y=82辆.可以得出车辆排队到达上游路口的时间为:取为

①当交通事故是在第一相位之前发生时

每个周期的前半个周期是第一相位，3分钟之内只有69辆车到达事故路段，82辆车中余下13辆要在下一个周期到达.第一相位发生的有19辆车可进入事故路段，剩下的13辆车全部是在下一周期第一相位时间内进入事故发生段，可得=0.35，排队到上游路口用t=3.35时分钟.

②当交通事故是在第二相位之前发生时

每个周期的前半个周期是第二相位，期间剩下的13辆车中有6辆车进入事故路段.另外7辆车在后半个周期到达事故路段.此时=0.68，排队到上游路口用 t=3.68时分钟.

2 总结

针对两个问题建立了两个模型，在建模过程中对缺失数据进行了差值处理，增加了模型的准确性，并且为了消除周期的影响，选取一分钟为单位时间统计路段的最大车辆数，具有一定的合理性.即得到了车道被占用对道路通行能力的影响.

［1］李家杰，郑义.影响城市道路通行能力因素分析［J］.城市道桥与防洪，2006，(03):225 －227，2006 年.

［2］吴立斌，等.MATLAB数据分析方法［M］.北京:机械工业出版社，2012:220－221.

［3］陆化普.城市交通现代化管理［M］.北京:人民交通出版社，1999:256－257.

［4］姜启源，叶俊，等.数学模型［M］.北京:高等教育出版社，2001:38－43.

［5］王连威.城市道路设计［M］.北京:人民交通出版社，2007:112－114.

［6］高海龙，王炜，等.无信号交叉口通行能力折减系数计算方法［J］.公路交通科技，2000，(05):70 －73.

［7］杨桂元，黄已立.数学模型［M］.合肥:中国科学技术大学出版社，2008:220－224.