高效双模逻辑机械综合传动技术研究

李慎龙，周广明，赵 凯，尹华兵

(中国北方车辆研究所车辆传动重点实验室，北京 100072)

当前液力机械综合传动系统效率低主要是由液力变矩器和转向泵/马达所造成的，液力变矩器最高传动效率为85%，高效工作区传动效率为80%;转向泵/马达最高机械效率为90%、容积效率为85%，总的效率仅为76.5%.同时由于液力变矩器和转向泵/马达存在多次能量形式的转化，所以很难进一步提升该传动元件的能量传递效率.传动效率低所带来的影响是多方位的、系统性的，包括增加了散热冷却系统负担、降低了系统高温环境的工作适应能力和车辆有效驱动功率利用率，且随着传动系统向高功率密度、高转速和高可靠性的发展需要，迫切需要降低传动系统的功率损失，提高传动效率.

据国外战车发展动态文献表明，美国地面车辆动力与机动性技术战略的中期目标(2017年)是32速双模逻辑综合传动装置.这种传动装置的特点有:无需液力变矩器;精确机械转向，无需大功率转向泵/马达;轻型紧凑设计;高负荷控制效率;传动效率高，大于90%;目前的研究产品包括西班牙SAPA公司SG-850双模逻辑变速器 (见图1)[1]和加拿大KerTrain研究所的双模逻辑变速器.

图1 SG-850双模逻辑机械综合传动装置

通过研究国外战车传动装置发展状况，提出了一种高效、多挡位、大传动范围的双模逻辑机械综合传动总体方案，建立了双模逻辑行星变速机构设计方法，完成了直驶和转向性能计算，并与液力机械综合传动进行对比分析，计算结果表明双模逻辑机械综合传动能有效提高发动机功率利用率和转向行驶稳定性.

1 系统结构组成及工作原理

双模逻辑机械综合传动的系统结构组成如图2所示，包括前传动、功率分流机构、起步离合器、直驶传动链和转向传动链的双模逻辑行星变速机构、汇流排等主要模块.可以看出，与液力机械综合传动系统最大变化在于:不再采用液力变矩器和转向泵/马达，而是通过能实现多挡位、大传动比范围的2个双模逻辑行星变速机构来代替.

1)直驶工况.

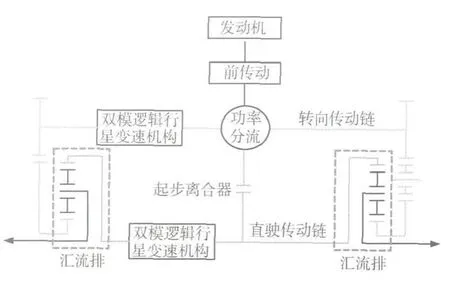
图2 系统结构组成

转向传动链的双模逻辑行星变速机构输出轴闭锁、输入轴能够自由旋转，通过直驶传动链双模逻辑行星变速机构换入不同挡位来满足车辆行驶速度和牵引力要求，发动机功率全部通过直驶传动链变速机构来传递到主动轮，其中直驶传动链双模逻辑行星变速机构的低挡位主要满足爬坡和困难路面行驶需要.

2)转向工况.

根据路面转向半径的不同将转向传动链双模逻辑行星变速机构换到某一挡位，实现零差速、多个理论规定转向半径的有级转向.其中，中心转向通过将直驶传动链双模逻辑行星变速机构输出轴闭锁来实现，发动机功率全部通过转向传动链变速机构来传递到主动轮.

根据双模逻辑机械综合传动的系统结构组成，对该传动系统与液力机械综合传动系统在某一转向工况下的传动效率作了一个简单对比，如图3所示.可以看出，双模逻辑机械综合传动总的效率能达到86.85%，而液力机械综合传动系统总的效率仅为69.84%.

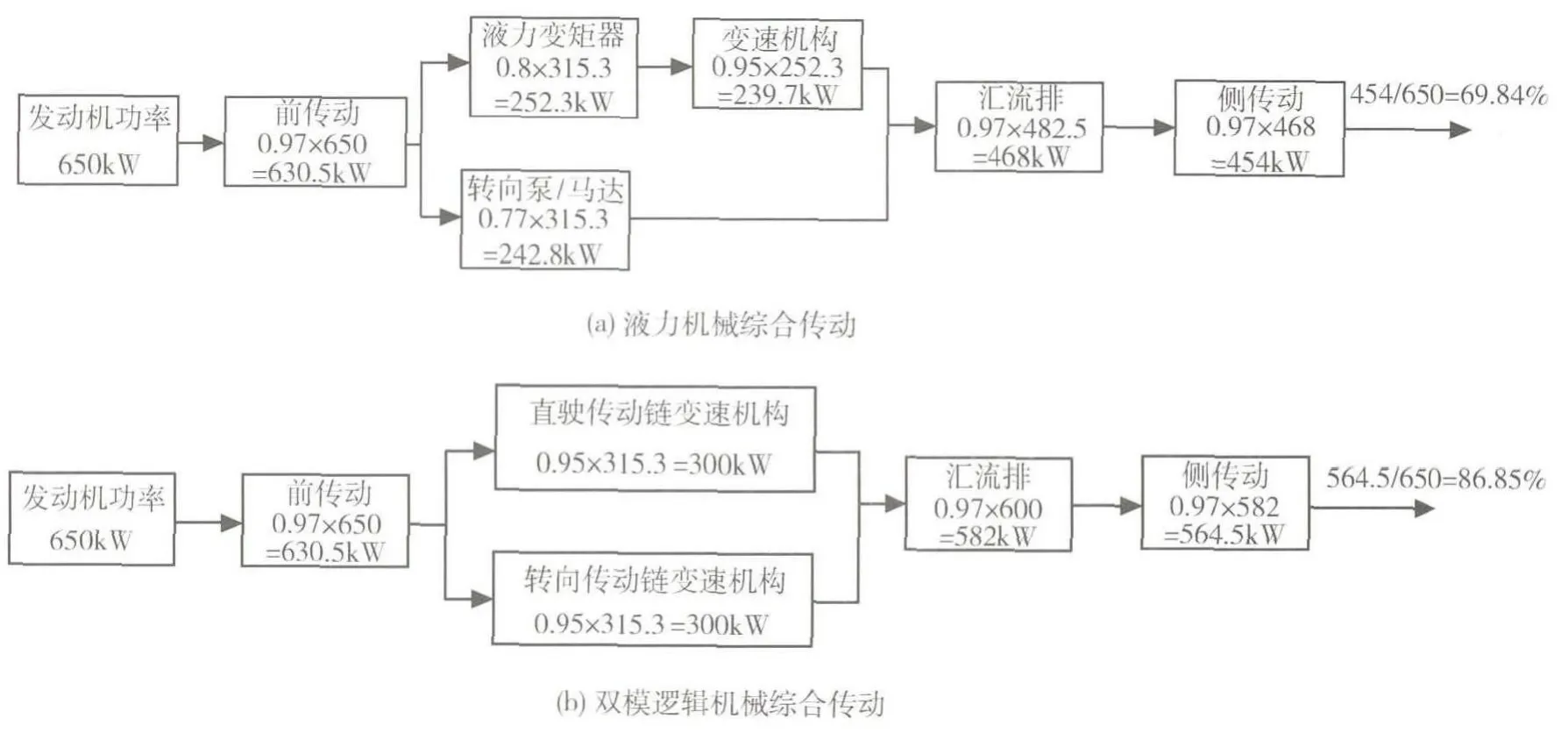
图3 传动系统总的传动效率对比

2 双模逻辑行星变速机构设计方法

双模逻辑行星变速机构，采用模块化的设计方法，即将n1个能实现2个挡位的二自由度行星排[2](见图4)或n2个能实现4个挡位的三自由度多元件复合排[3](见图5)等基本行星传动模块串联而成，从而实现Nx个挡位数量.

图4 实现2个挡位的二自由度行星排

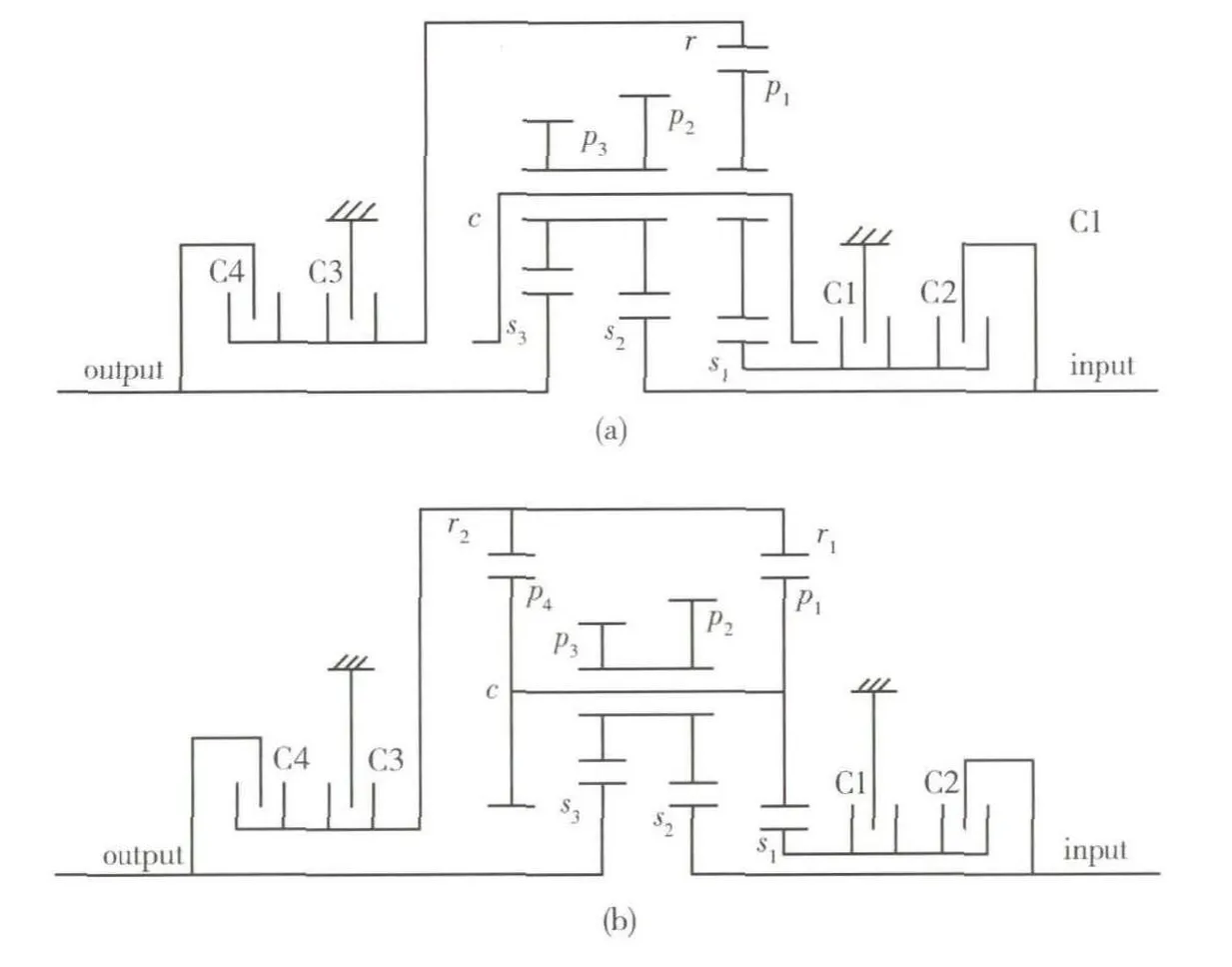
图5 实现4个挡位的三自由度多元件复合排

利用多自由度行星传动理论[4]，以图4(a)和图5(a)为例，对上面基本行星排模块各挡位能实现的传动比进行了计算.计算公式如式(1)～式(11).

1)图4(a)行星变速机构方案.

行星排三元件转速关系:

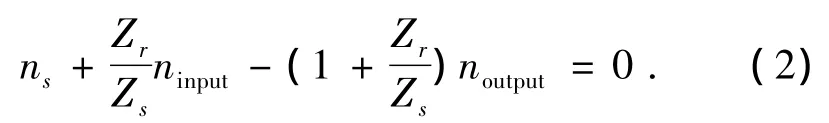
1挡 (C1接合):

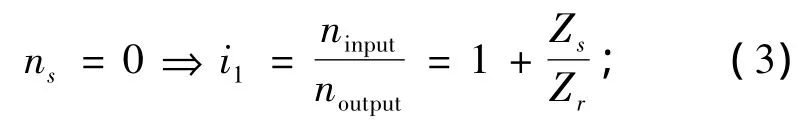
2挡 (C2接合):

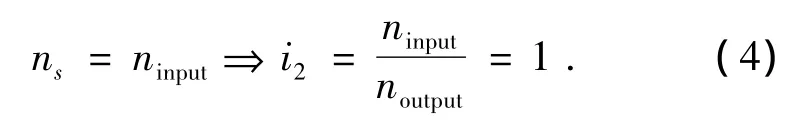
式中:ns、ninput、noutput分别为行星排太阳轮、输入轴、输出轴的转速;Zs、Zr分别为行星排太阳轮、齿圈的齿数;i1、i2分别为1挡、2挡的传动比.

2)图5(a)行星变速机构方案.

2个行星排三元件转速关系:

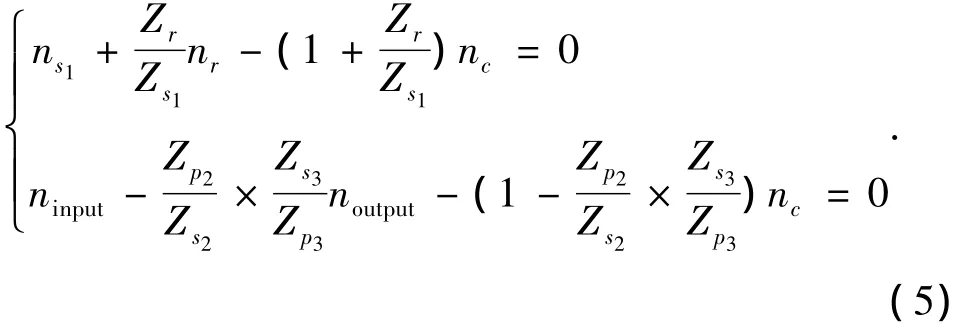
1挡(C1、C3接合):

2挡(C1、C4接合):

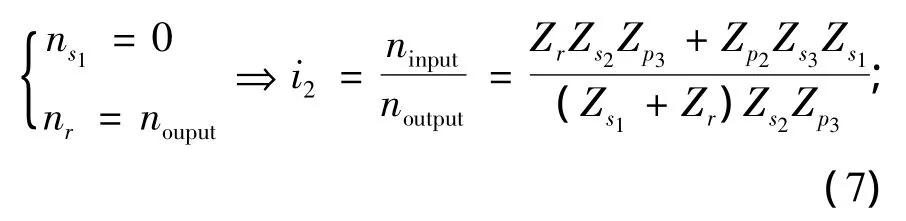
3挡(C2、C3接合):

4挡(C2、C4接合):

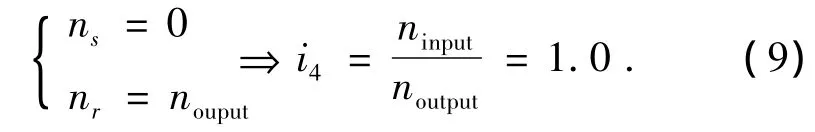
式中:ns1、nr、nc、ninput、noutput分别为行星排太阳轮s1、齿圈、行星架、输入轴、输出轴的转速;Zs1、Zs2、Zs3、Zp1、Zp2、Zp3、Zr分别为行星排太阳轮s1、太阳轮s2、太阳轮s3、行星轮p1、行星轮p2、行星轮p3、齿圈的齿数;i1、i2、i3、i4分别为1挡、2挡、3挡和4挡的传动比.

双模逻辑行星变速机构各挡传动比是以传动比范围为依据，采用等比级数划分方式来制定.为了满足该划分方式各挡传动比要求，充分利用行星排和操纵元件，要求所组成的基本行星排主传动比必须满足一定的要求.由2挡的二自由度基本行星传动单元集成变速机构的阶比与各行星传动单元特征参数计算公式为

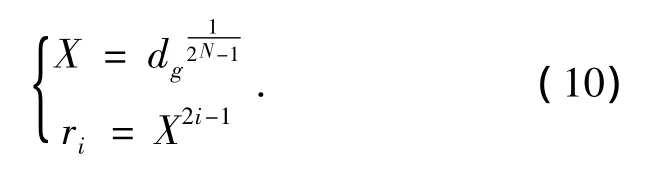
由4挡的三自由度基本行星单元集成变速机构的阶比与各行星传动单元特征参数计算公式为

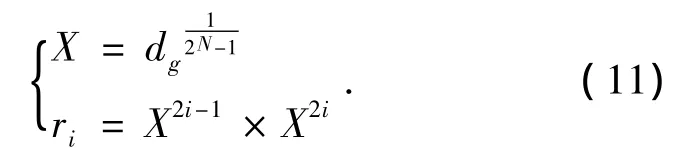
式中:X为相邻挡位的阶比;ri为第i个基本行星传动单元特征参数;dg为变速机构的传动比范围;N为组成变速机构的基本行星传动单元数量.

3 双模逻辑行星变速机构工作原理

通过上面分析可知，双模逻辑行星变速机构是由多个基本行星排串联而成.下面结合实际设计要求，以实现传动比范围18为设计依据，通过5个上面给定的2挡二自由度基本排串联，则该变速机构可以实现32个挡位，对应传动方案简图和传动装置简图分别如图6和图7所示，对应的换挡逻辑为

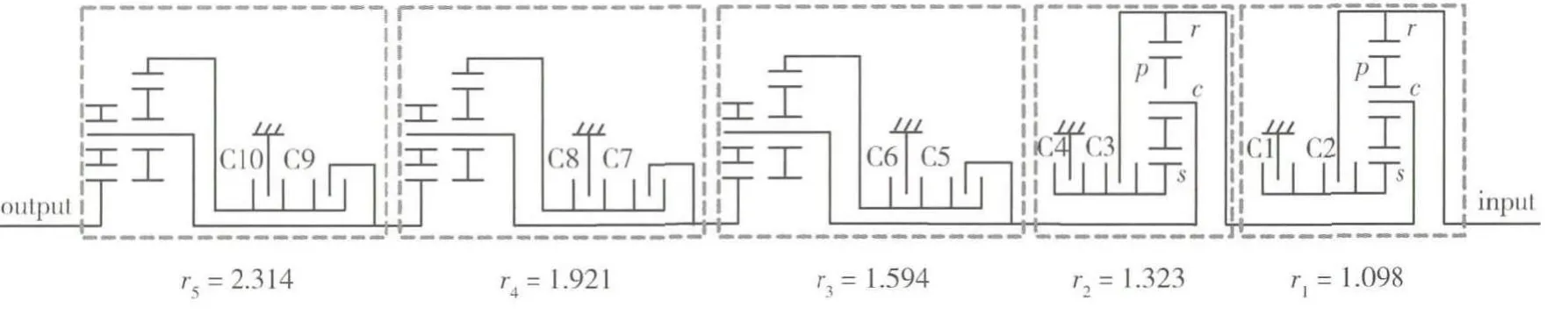
图6 32挡双模逻辑行星变速机构传动方案

图7 双模逻辑变速机构装置

对每个基本行星排实现1挡传动比定义为逻辑“1”，实现2挡传动比定义为逻辑“0”，即整个机构整体回转.表1给出了该32挡双模逻辑行星速机构各挡换挡逻辑，以及对应的传动比.可以看出，该类变速机构换挡逻辑类似于连续的二进制代码，故称为“双模逻辑变速机构”.

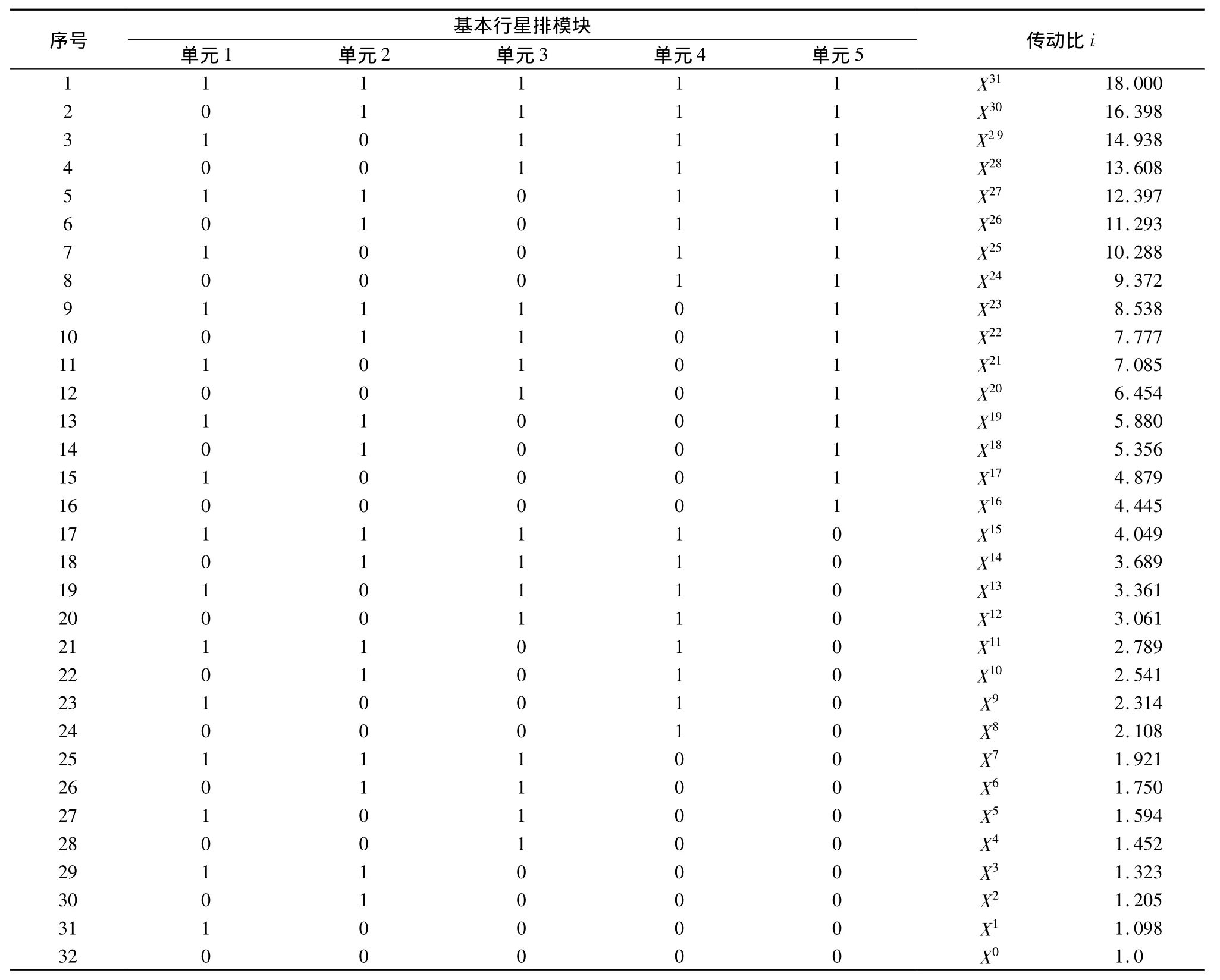
表1 双模逻辑行星变速机构换挡逻辑

4 性能分析

4.1 直驶牵引性能计算

对双模逻辑机械综合传动直驶牵引力、牵引功率和动力因数等方面进行分析，计算结果如图8、图9所示.可以看出:该传动系统牵引特性非常接近理想特性 (低速恒牵引力、高速恒牵引功率)，发动机功率利用率达到了90%以上;与液力机械综合传动系统对比表明，该传动系统能够有效提高发动机功率利用率，优化发动机运行工作点.

图8 车辆牵引力、牵引功率与车速变化曲线

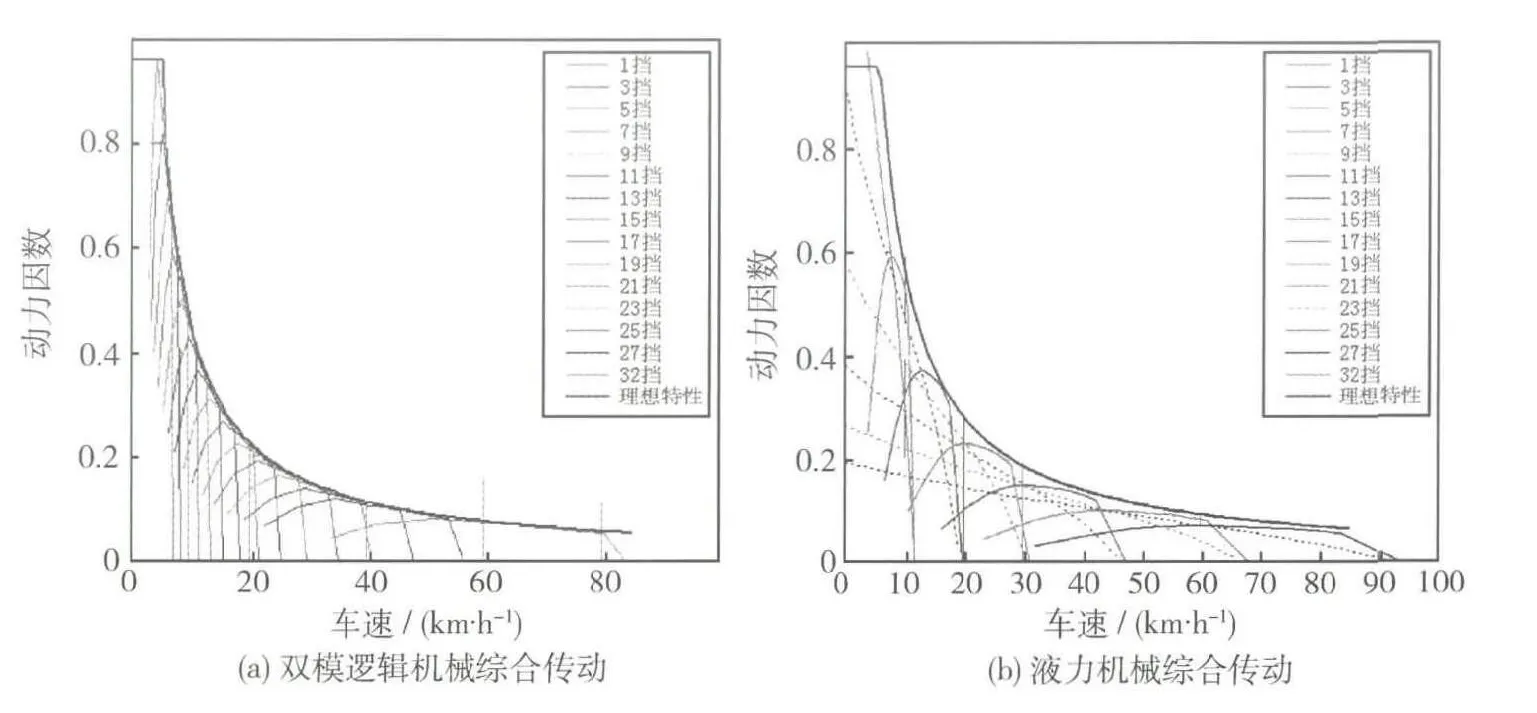
图9 车辆动力因数与车速变化曲线

4.2 转向性能计算

对双模逻辑机械综合传动的转向性能进行了分析，该系统对于每个挡位而言有32个理论规定半径，这些规定半径能够覆盖车辆整个转向域，其转向机动性能与转向泵/马达零差速无级转向相当.对直驶传动链每挡位下的所能实现理论转向半径和转向传动链相对分流功率的匹配模型进行推导，得到了相对应的变化规律，如图10所示.

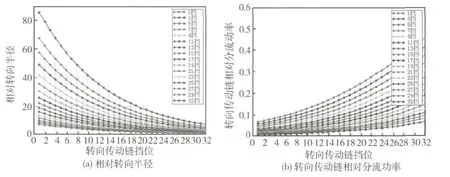
图10 相对转向半径、转向传动链相对分流功率与转向传动链挡位变化关系

可以看出:转向传动链在低挡位下相对转向半径较大，高挡位下具有较小的相对转向半径，与转向传动链所处挡位状态呈递减变化;低挡位下相对分流功率较小、高挡位下相对分流功率较大，与转向传动链所处挡位状态呈递增变化.

式中:iz为转向传动链双模逻辑变速机构传动比;im为转向传动链双模逻辑变速机构输出轴至汇流排太阳轮的传动比;kh为汇流排主传动比;ib为直驶传动链双模逻辑变速机构传动比;ρ为相对转向半径;Prev2为转向传动链相对分流功率.

进一步推导出转向传动链和直驶传动链相对分流功率随相对转向半径变化关系模型，以及相对变化关系，如图11所示.

图11 转向传动链和直驶传动链相对分流功率与相对转向半径变化关系

可以看出:转向传动链相对分流功率随相对转向半径增加而减小，直驶传动链相对分流功率随相对转向半径增加而增大.

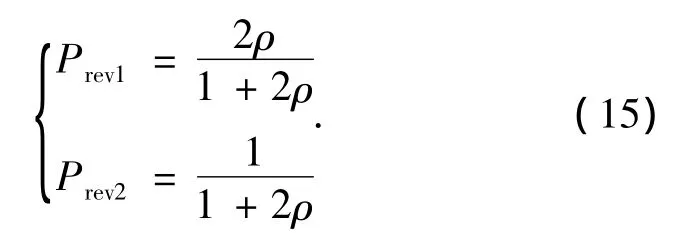
式中:Prev1为直驶传动链相对分流功率.

5 结论

1)建立了双模逻辑机械综合传动的系统结构组成，分析了该传动系统各种工况的工作原理.

2)双模逻辑行星变速机构是由多个二自由度或三自由度的基本行星传动模块串联而成，可实现模块化设计.需要突破多构件复合行星排运动学和动力学分析与验证技术;以及新型多锥换挡元件设计技术，为结构紧凑双模逻辑行星变速机构研制提供技术支撑.

3)双模逻辑机械综合传动在传动效率、发动机功率利用率、换挡冲击、转向行驶安全性和侧倾坡直驶稳定性等方面具有较大技术优势;在转向机动性能方面与当前液力机械综合传动系统相当.

[1] John H.Kerr.Incrementally Variable Tranmission:Canada，4559848[P].1985-12-24.

[2] 刘修骥.车辆传动系统分析[M].北京:国防工业出版社，1998.

[3] 闫清东，张连第，赵毓芹，等.坦克构造与设计[M].北京:北京理工大学出版社，2006.

[4] 万耀青，刘太来.行星变速箱方案选择理论与优化[M].北京:国防工业出版社，1997.

[5] John H.Kerr.Coplanar Reverted Gear Train Loop:Canada，6126566[P].2000-10-03.

[6] John H.Kerr.Concentric V-groove Coupling:Canada，0061485[P].2011-03-17.