解析法在行星变速机构效率和功率流分析中的应用
2014-08-21邢庆坤赵欣源
邢庆坤,赵欣源,张 鹤,何 融
(中国北方车辆研究所车辆传动重点实验室,北京 100072)
行星变速机构与定轴变速机构相比,有诸多明显的优点,关于行星变速机构的效率问题,国内外很多学者都在积极地进行探索与研究,发表了许多关于效率计算方面的论文.尽管使用方法和技巧各个不同,但归纳起来主要是由两种方法推导或者派生出来的,一个是相对功率法[1](也称啮合功率法),一个是转化机构法 (也称换算机构法).应用相对功率法计算效率时基于两个前提:1)行星轮做牵连运动和相对运动时分别产生牵连功率和相对功率,只计算与相对运动有关的功率损失,忽略牵连运动产生的功率损失;2)行星变速机构相对运动产生的齿轮啮合损失与定轴相同.转化机构法最早见于1965年前苏联克列依涅斯所著的文章[2],克列依涅斯运用对分效率求偏导数的方法解决了转化机构法中相对功率流向的判断问题,并提出了各种不同类型周转轮系的效率计算的通用方法.
这两种方法相比各有优缺点,在只考虑轮齿啮合损失的前提下,用相对功率法求得的效率是近似的,用转化机构法求得的效率是精确的.前者对于已经完成运动学与动力学分析的方案有无可比拟的求解优势,可以直接利用运动学及动力学运算结果进行效率分析,在一定的情况下具有足够的精确度.这两种方法均没有将效率求解与结构分析联系在一起,不能在设计者选择行星变速机构方案以提高传动效率时起到指导作用,同时后者在进行功率流向的判断时,需要一定的技巧,不便于一般工程技术人员的掌握与使用.
在功率流分析方面,常规的分析方法为先进行运动学与动力学计算,最后通过构件转速与扭矩的方向的异同来确定,过程比较繁琐,若进行功率分析必须进行相应的运动学和动力学计算.刘修骥教授提出应用符号法判断功率流向[3],但这种方法仅能应用于一部分特定方案.吕粟樵教授应用大小力矩构件的性质提出功率流分析的快速判断方法[4],但此方法仅限于三排以下的行星变速机构方案才能应用,同时,判断依据分类较多,并不容易掌握.
本文所介绍的方法在本质上属于啮合功率法,在效率的最终结果表示上,却表现为与转换机构法求得的效率表达式相同的构式,是对啮合功率法与转换机构法的延伸与发展.此方法可以对任意复杂程度的多自由度行星变速机构方案进行效率分析,此外,运用此方法还可以对行星变速机构的方案进行功率流分析,判断是否存在循环功率及计算循环功率在输出功率中所占的比例,同时还对选择传动方案具有指导意义[5].
1 基本行星排结构分析
行星变速机构以行星排为基本单元,行星排都具有对外联系的3个构件——行星架、齿圈和太阳轮以及只做内部联系的元件——行星轮,行星轮不是构件,但却是行星排的内在核心.基本行星排的构成元素有两种运动方式:中心轮围绕行星排轴线的旋转运动和行星轮的行星式运动 (绕行星排轴线旋转运动和绕自身轴线旋转运动的合成运动).
为了方便叙述,我们根据行星排的运动特性引入基本回路的概念.所谓基本回路是由3个行星排的构成元素 (我们称之为链)组成,这里所说的构成元素不但包括行星排的构件也包括行星排的元件,也就是说,链既可以是齿圈、太阳轮、行星架,也可以是行星轮.每个基本回路由3个元素组成:相互啮合的一对齿轮以及使这对啮合齿轮的中心保持固定距离的行星架.
下面我们对7种基本行星排进行基本回路分析.7种基本行星排结构及编号如图1所示.7种基本行星排的基本回路分析如表1所示.
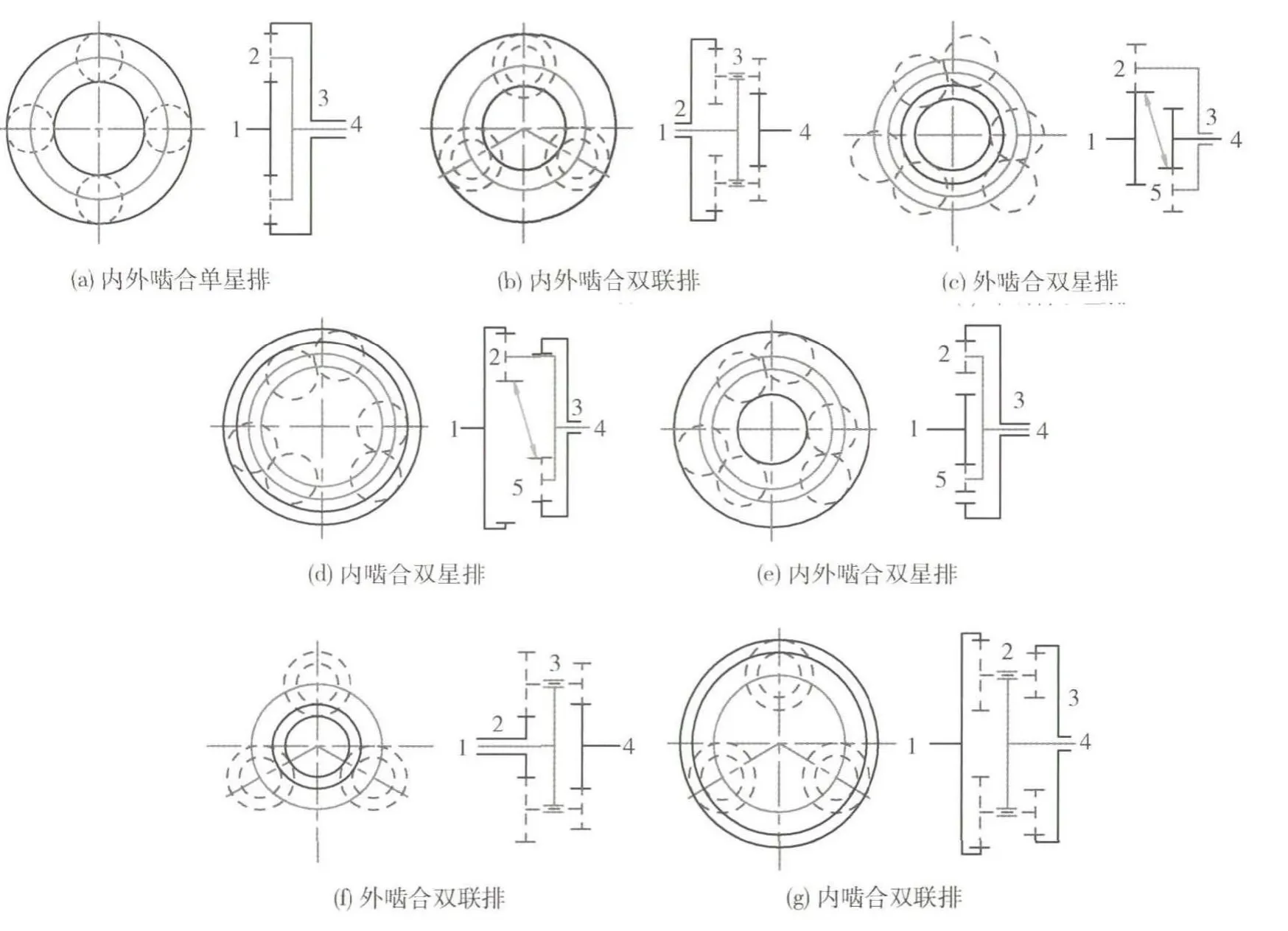
图1 7种基本行星排结构及编号

表1 7种基本行星排基本回路分析
通过分析,我们不难发现:
1)对于一个行星变速结构,基本回路个数=链的个数 -2[6];
2)每种基本行星排只有一个行星架,并且行星架包含在每一个基本回路中作为链存在;
3)基本回路的个数等于结构中啮合齿轮对数目,这里所说的啮合齿轮对数目不包括为了平衡结构而加入的行星轮齿轮对.
任何一个复杂的行星变速机构方案都是由上述的7种基本行星排的一个或几个进行有序的排列组合而成的,图2为某车行星变速箱方案在实现某挡位时的方案简图.
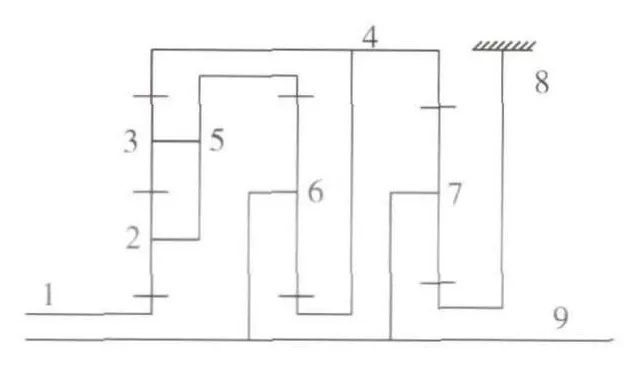
图2 某行星变速箱实现某挡位方案简图
不难看出,此方案包括3个基本行星排,1个内外啮合双星排(图1(e))和2个内外啮合单星排(图1(a)).由前面分析可知共有7个基本回路.根据图2编号,1为输入端,9为输出端,8为制动端.基本回路及链分析如表2所示.
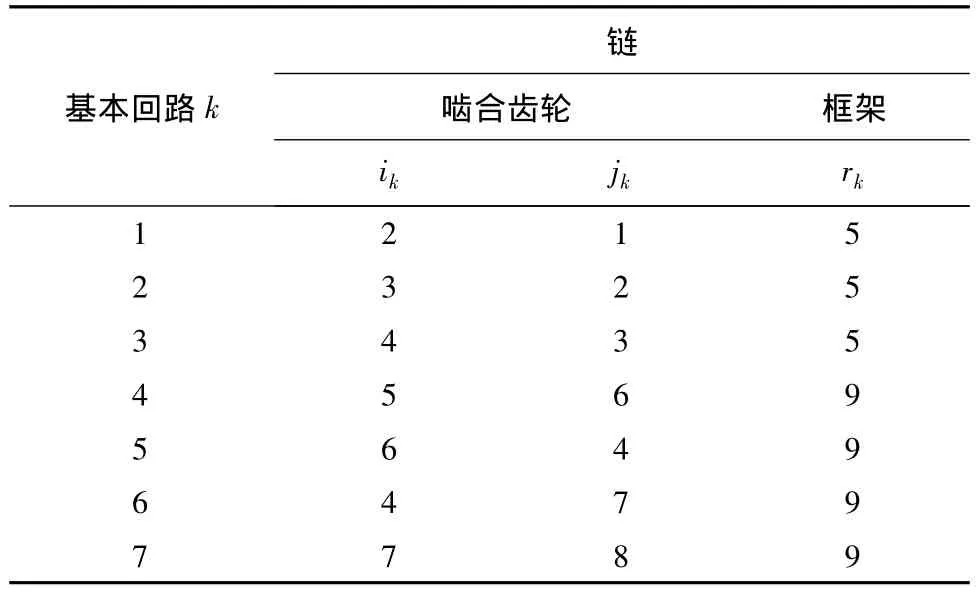
表2 基本回路组成
下面我们即以此例进行效率与功率分析.
2 理论转速与扭矩分析
一个行星变速机构方案是由数个基本回路组成的,基本回路特征参数Zk定义如下:

式中:“+”对应于基本回路中的啮合齿轮对属于外啮合,“-”对应于基本回路中的啮合齿轮对属于内啮合.
根据行星排的运动关系易知,

式中:ωik、ωjk和ωrk分别是指基本回路k中的链i、j、r的角速度.
当行星机构平稳工作时,若不考虑功率损失,那么基本回路中的链所受外力矩代数和为零,所传递的功率代数和亦为零,即
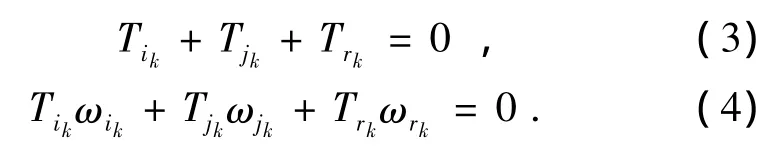
将式(3)与式(2)代入式(4),消去关系式中的r因子,得到
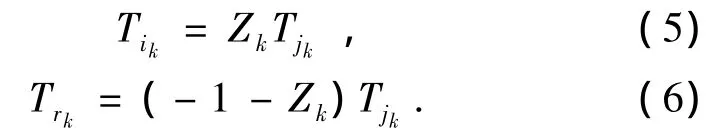
同时,对于每一个基本回路中的链,其受到的外力矩之和为零,对于链n,我们可以写出下面等式:
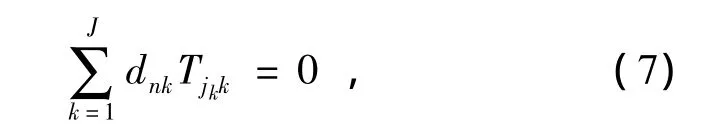
其中
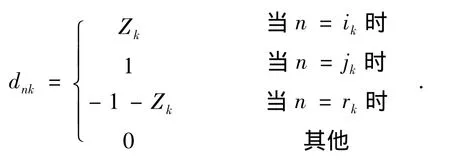
显然,这里的链n不能是输入构件、输出构件或者制动构件.
这样dnk可以形成一个N×J的矩阵D,其中N是行星变速机构中链的总个数,J为基本回路的总个数.
由式(2)我们可以得到:
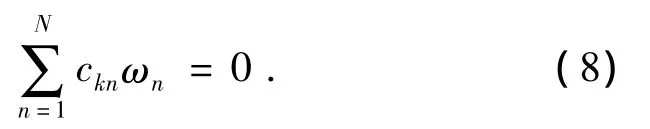
式中:ckn形成J×N矩阵C,其中ckn=dnk,C和D 互为转置矩阵[7].
我们定义TREAC,TOUT为制动构件、输出构件所受力矩,此外,我们规定输入构件受外力矩为1,于是我们可以得到力矩关系矩阵:
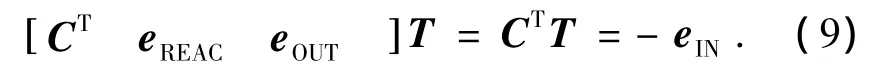
为了保持转速与扭矩的系数矩阵依然保持转置关系,而只需要在等号右边改变常数矩阵,我们引入列矩阵Ω-,使满足:
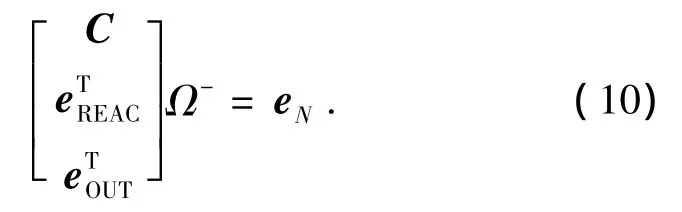
其中,eN为单位矩阵,只最后一个元素为1.对比式(10)与式(9),不难发现Ω-的实际意义,即式(10)中,我们将原行星变速机构的输出转速规定为单位值1,同时Ω-与Ω关系为:

根据图2与表2,我们根据实际齿轮齿数计算得到各基本回路特征参数,如表3所示.

表3 基本回路特征参数
依据上述分析,可得到已知量:
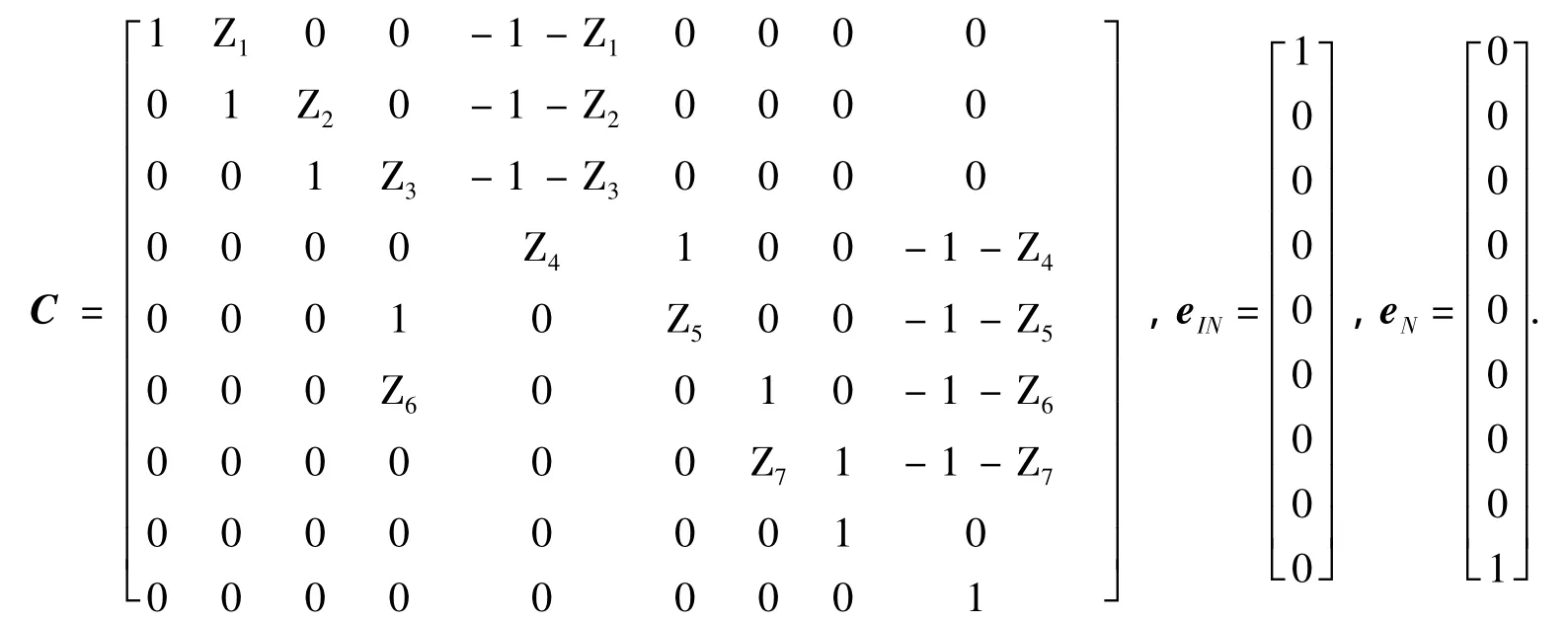
未知量为:
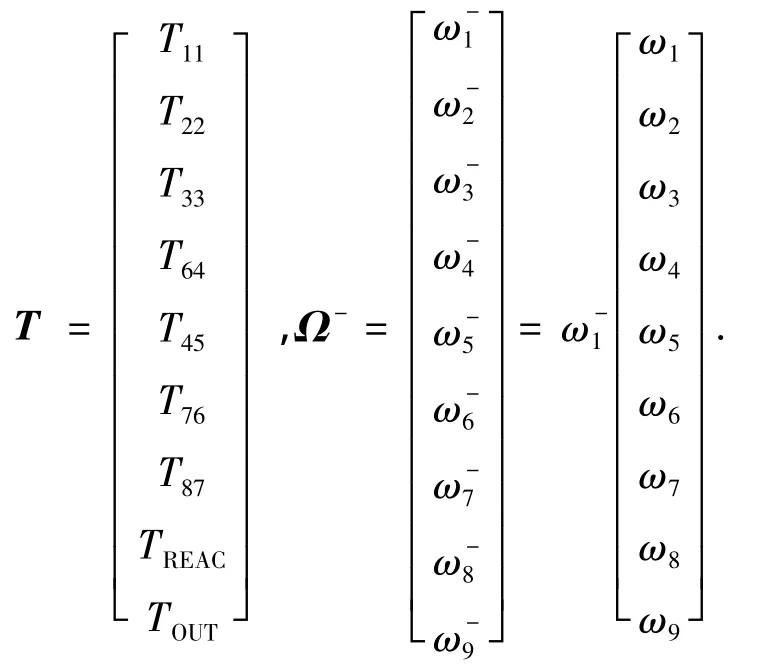
根据式(9)和式(10),可解得结果的符号表达式及值,如表4、表5所示.

表4 角速度结果 (rad ·s-1)
其中:
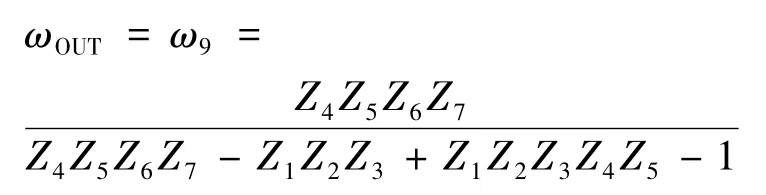

表5 力矩结果 (N·m)
3 效率分析
当考虑行星变速机构齿轮啮合损失时,式(4)将不再成立.现假设在一个基本回路中,i是主动轮,式(4)可写为式(12).

这里ηk的物理含义为当行星排框架相对静止时基本回路k在传递功率时的效率.此时已经将行星排的传动效率等同于定轴齿轮传动时的效率,ηk的值与齿轮的材料、制造误差、油温与润滑条件有关.根据我国目前的齿轮加工精度、制造条件,通常内啮合取0.98,外啮合取0.97.
联立式(2)与式(12),可得:

当j是主动轮时,

为统一公式,我们引入:
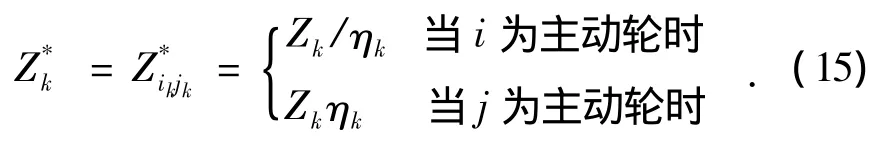
这样,无论i是主动轮还是被动轮,我们可以得到统一的表达式
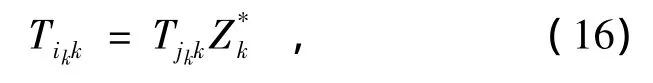
以及
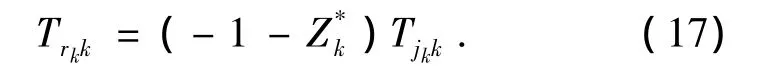
这样,式(9)与式(10)中、以及理论计算中由Zk表示的扭矩系数矩阵和转速系数矩阵最终都将可以由来表示.
由于我们规定了输入转速与扭矩为1,所以最终行星变速机构的效率即为

解式(9)、式(10)得:

现在求效率的关键归结为判断在行星排的相对运动中确定组成环元素的链的主被动的问题.
显然,主动齿轮所受的内力矩与转速方向相反,即当i在行星排相对运动中为主动轮时,
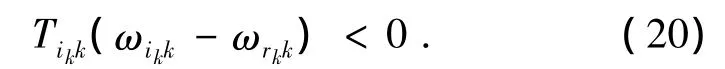
此时啮合功率从i流向j,根据式(15)即可得出行星变速机构的传动效率.
事实上,文献[8]已经证明
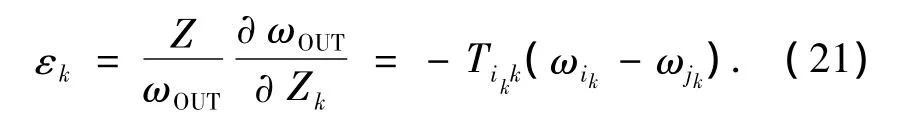
我们称εk为灵敏度度系数.若εk>0,则i为主动.表6为灵敏度系数计算结果.
此外还可以通过式(22)来判断啮合功率流的方向[8].
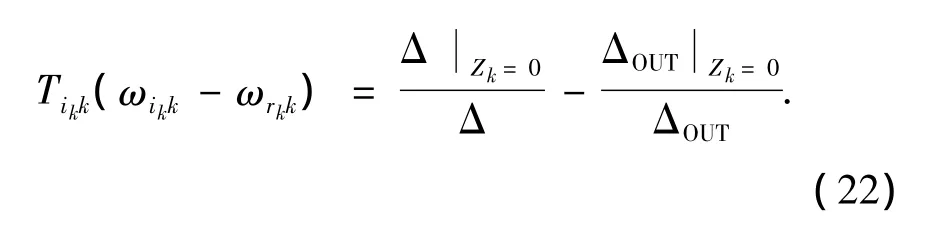
其中Δ =det(C),ΔOUT是根据Cramer’s Rule将Δ对应的输出列以单位列向量代替得到的行列式.
内销局面依然不佳。近期国内尿素市场暂无“亮点”,因高价风险不容忽视,下游经销商近段时间内除随进随出操作外,备肥或者说淡储需求继续推迟。多数省级大农资公司前期库存成本价在1950-2000元/吨,再度考虑备肥的心理价位势必在2000元/吨以下,且与工厂存在一定议价默契,对尿素企业来说自然也将是后期吸单的筑底机会。工业需求方面显然也没能借到磷复肥会议的“春风”,复合肥企业整体开工率依然偏低。另外,受环保检查影响,尿素限产,下游胶合板企业也已被降产,原料采购同时缩减。总之,整体内需启动缓慢,降价或为最好刺激。

表6 灵敏度系数εk计算结果
结合表6,根据式(15)及式(19)即可进行效率计算:

当内啮合取0.98、外啮合取0.97时,可计算得到η =91.12% .
4 功率分析
为了进行比较,我们先运用符号法进行功率流的判断.“⊕”代表扭矩为正,“+”代表转速为正.当一个构件端扭矩与转速方向相同,则从该端输入功率.
符号法判断原则如下:
1)同构件上任何点,转速相同;
2)同一构件受两个力矩,方向必相反;若同一构件三个点受外力矩,若两点相同,则第三点必相反;
3)同一行星排中,太阳轮所受力矩、齿圈所受外力矩和行星架所受外力矩三者符合关系式Tt∶Tq∶Tj=1∶k∶[-(1+k)],其中k为行星排内传动比[1].
我们也可以试着运用吕粟樵教授的大小力矩构件性质判断方向,对应方案图我们得到连接图,如图4所示.
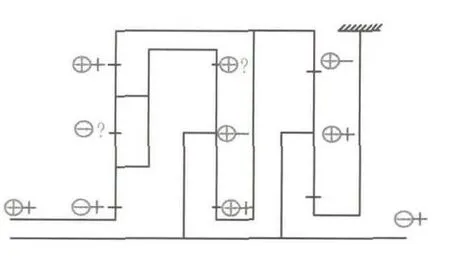
图3 符号法功率流分析图

图4 连接关系图
根据文献[4]所述,可能的功率流路线如图5所示.构件连接有双向箭头代表功率流向未明.由排列组合可知,共可能有29-1种情况,需要根据大小力矩的判断规则去一一判断,显然这是非常繁琐的.正如其说述,必须要通过运动学与动力学计算进而判断功率流向.
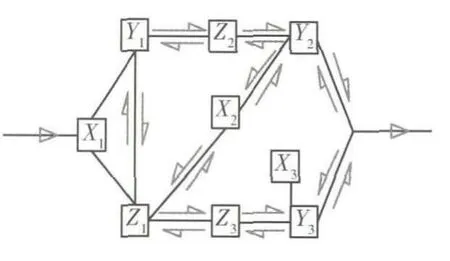
图5 功率流向图
由以上分析可知,对于复杂的行星变速机构方案简图,以上两种方法并不能解决功率流向的判断问题,无法得到是否存在功率循环,进而确定其循环功率的比例更无从谈起.实际上,运用解析法判断功率流向优势非常明显,下面予以说明.
上面我们已经分析式(20)是判断啮合功率流向的根本依据,但应该注意到这里说的啮合功率与实际功率是两个概念,从这里不能得出整个行星变速机构的总的实际功率流向,也不能判断是否存在循环功率.
实际上功率的流动是通过齿轮的啮合传递的,判断功率流的方向即可以从齿轮的啮合出发,判断依据如下:
若sgn(Tjkk)与sgn(ωjkk)相同,则 i为主动,实际功率从齿轮i流向齿轮j;若相反,则实际功率从齿轮j流向齿轮i.
下面我们对上述方案进行分析.
根据表7,容易得出此挡位的功率流图,如图6所示.
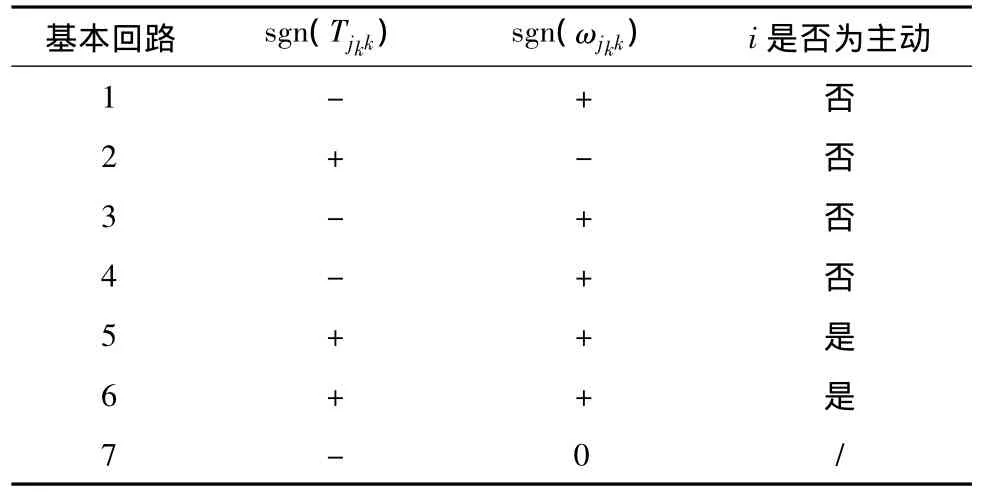
表7 符号对照表
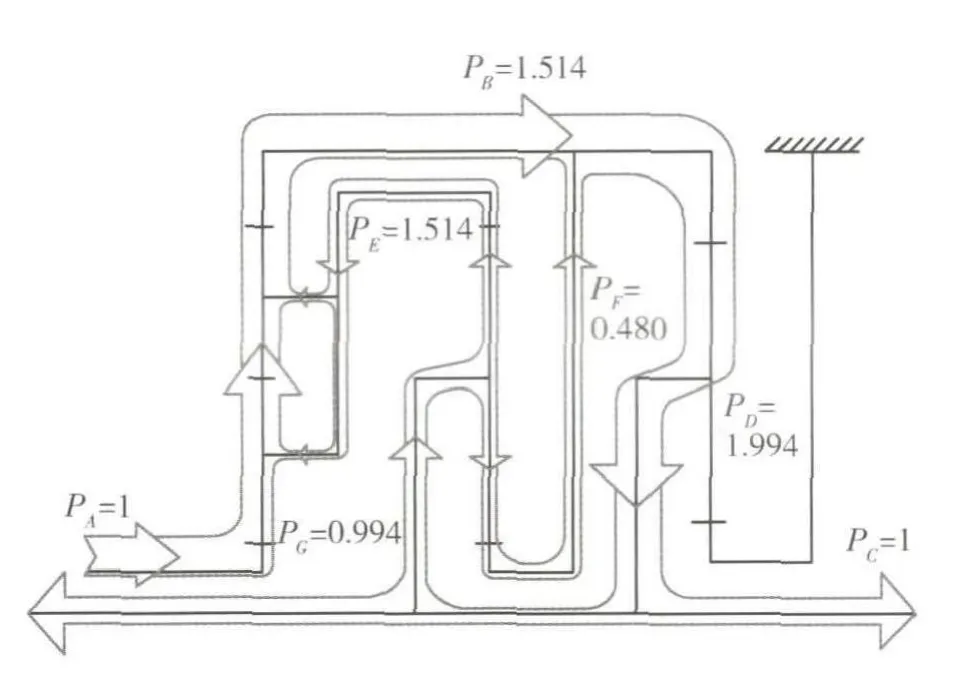
图6 功率流向图
设输入端A所受力矩为单位1,转速为单位1,输入功率PA=1,若不考虑功率损失,则输出端C输出功率PC=1,一排齿圈流入功率PB=1.514,三排齿圈流出功率为PD=1.994,二排行星架流入功率PG=0.994,一排行星架流入功率PE=0.514,二排太阳轮流出功率为PF=0.480.
从图6可以看出,整个系统中共有两个功率流。我们将从输入端A至B,然后到C流出的功率流称为主功率流;将从G处流入二排框架的功率称为循环功率流.被动件有3个受力点:D、G和C,其中D为输入,G、C为输出,功率在此处分流.功率流至第二排框架时功率重新分流为两部分,一部分流经第二排齿圈与输入功率在第一排齿圈处汇流;一部分流经第二排太阳轮,与从第一排齿圈处流经的功率在第三排齿圈处重新汇流.循环功率的存在使得B处构件承载的功率增大,但增大的功率并没有输出,反而使这些环节的构件所受的强度增大.同时考虑到实际机构中摩擦必然存在,循环存在的功率必然消耗能量,功率损失也势必增大,因此循环功率是需要尽量避免的.是否存在循环功率也是判断方案优劣的一个重要标准.此方案的循环功率所占的比例可以用 PG/PD来计算,即:
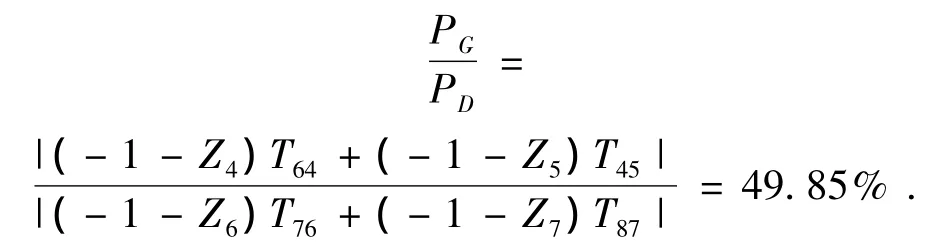
5 结论
运用解析符号法能够求解任意复杂程度的行星变速机构的效率,能够进行快速地判断功率流,能够判断是否存在功率循环以及循环功率所占的比例.
此方法与其他方法所得结果是一致的,根据表2中基本回路i、j的定义方式与k的定义方式[1],不难看出:Z1Z2Z3=k1,同理 Z4Z5=k2,Z6Z7=k3.于是
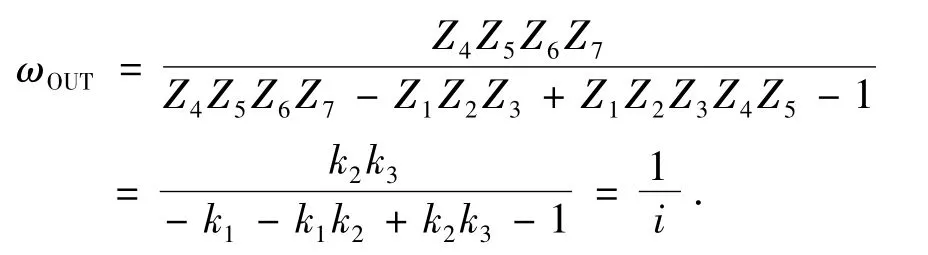
至于效率表达式:
此方法得出的功率流图,也与常规求解法先进行运动学与动力学计算然后应用符号法得出的结果相同。
[1] 万耀青,刘太来.行星变速箱方案选择理论与优化[M].北京:国防工业出版社,1997.
[2] Крейнес М А,Розовский М С.Зуочатые,механизмы[M].Москва ИМУ,1965.
[3] 刘修骥.车辆传动系统分析[M].北京:国防工业出版社,1998.
[4] 吕粟樵.拖拉机常用行星轮系循环功率之快速判断[J].拖拉机与农用运输车,1981,(2):35-41.
[5] H.I.Hsieh,L.W.Tsai.The selection of a mostefficient clutching sequence assoc-iated with automatic transmission mechanisms[J].ASME Journal of Mechanical Design,1998,(120):514 -519.
[6] F.Buchsbaum,F.Freudenstein.Synthesis of kinematic structure of geard kinematic chains and oher machanisms[J].Journal of Mechanisms,1970,(5):357 -392.
[7] D.J.Sanger.Matrix methods in the analysis and synthesis of coupled differential mechanisms[C].//Proceedingsof the 4th World Congress on the Theory of Machinesand Mechanisms.Newcastle,UK,1975:27-31.
[8] Jose M.del Castillo.The analytical expression of efficiency of planetary gear trains[J].Mechanism and Machine Theory,2002,37:197 -214.
