液压挖掘机的动应力测试与瞬态分析*

任志贵 陈进 王树春 庞晓平 黄定红 马金成

(重庆大学 机械传动国家重点实验室，重庆 400030)

随着液压技术的发展，近50年来液压挖掘机在建筑、采矿、林业和土方作业中发挥着越来越重要的作用［1-3］.由于挖掘作业的高度复杂性、挖掘对象的不确定性和操作方式的多样性，挖掘机的可靠性和结构强度成为设计人员和用户最为关心的问题.在已知载荷和边界条件的情况下，有限元分析是强度计算最常用的方法［4］.静态分析方面:陈进等［5］利用Pro/E 计算出工作装置各构件在其最不利工况下的铰点力，利用Ansys 对其进行了强度和刚度分析并与静应力的测试结果作了对比验证;周宏兵等［6］利用Matlab 实现了任意载荷方式和挖掘姿态下铰点力的求解，并利用命令流在Ansys 中实现了多工况的静强度分析;为避免将工作装置各构件单独分析时因简化而造成的误差，杜文靖等［7-8］从系统集成角度整体建模，进行了特定工况的静强度分析;Tian 等［9］建立了工作装置在4 种特殊工况下的有限元模型，找到应力集中的薄弱部位，并进行了结构优化.

然而，挖掘机作为重型机械，长期在严酷的工作条件下连续工作，其载荷突出的动态特性和随机特性，是其机构和结构失效的成因［10］.动强度分析方面:程珩等［11］通过应变测量得到工作装置薄弱部位的载荷历程，利用雨流计数统计确定了S-N 曲线，并估算出各构件的疲劳寿命;张卫国等［12-13］基于测试数据，以最大理论撞击力作为驱动，利用Admas 仿真各铰点的受力，并进行瞬态动力学分析和疲劳寿命分析;但文献［12］中将静态力矩平衡原理用于动态撞击过程，结果6吨的挖掘机有350kN 的撞击力，说明该方法不能得到准确的载荷.同样，以往对挖掘机工作装置的强度分析中，也都是因为忽略了挖掘过程的动态特性，从而无法保证载荷计算的准确性.另外，实际的挖掘过程是动臂、斗杆和铲斗共同参与随机组合并与土壤相互作用的复杂过程.由经验丰富的司机进行有目的性的实地作业才是挖掘机的工作常态.但目前未见关于常态挖掘过程工作装置动态特性研究的相关文献.因此，文中根据达朗贝尔原理考虑惯性力和动力学特性，计算出真实挖掘过程的动载荷，并利用瞬态分析得到工作装置各构件整体的动应力特性.

1 动应力的测试

1.1 测点的布置及应变片的选择

挖掘机工作装置(动臂、斗杆)是由板件焊接而成的箱形结构，通常承受的外载荷可以分为轴力、弯矩和扭矩三类［14-15］.由于其纵向尺寸远远大于横截面尺寸，再加上扭矩本身较小，故轴力和弯矩引起的应力构成了工作装置横截面应力的主要部分.对于箱形截面而言，轴力和弯矩引起的应力叠加使得工作装置横截面的最大应力往往发生在截面角点位置.因此，为了测得挖掘过程中较大的结构应力，测点的选择应遵循以下原则:①测点尽量靠近所在横截面的角点;②测点布置于静强度分析中应力较大的位置;③测点布置于客户反馈的同款机型曾经发生破坏的位置.

挖掘机工作装置受力情况复杂，其构件主应力方向难以预知.因此，文中采用45°直角型应变花分别测量0°、45°和90°方向上的应变，进而计算测点的主应力及当量应力.应变花的桥接方式为1/4 桥接法，并用补偿线对导线电阻进行补偿.

1.2 测试流程

多种数据同步采集测试流程如图1 所示，采用45°直角型应变花获取工作装置对应测点的应变信号，采用NS-RB 型角位移传感器获取角位移信号(动臂与停机面间角位移θ1、斗杆与动臂间角位移θ2、铲斗与斗杆间角位移θ3)，采用NS-F 型压力传感器获取液压缸有杆腔和无杆腔的压力信号.使用一台DRA-30A 多通道动静态应变仪和一台NSDAC3000 数据采集测控系统同步采集10 个测点的动应变、3 组角位移和6 组压力信号.其中，角位移信号的获取是为了确定挖掘姿态，压力信号的获取是为了求解挖掘阻力和各构件铰点力，而挖掘姿态和铰点力的时间历程可用于后期的瞬态分析.

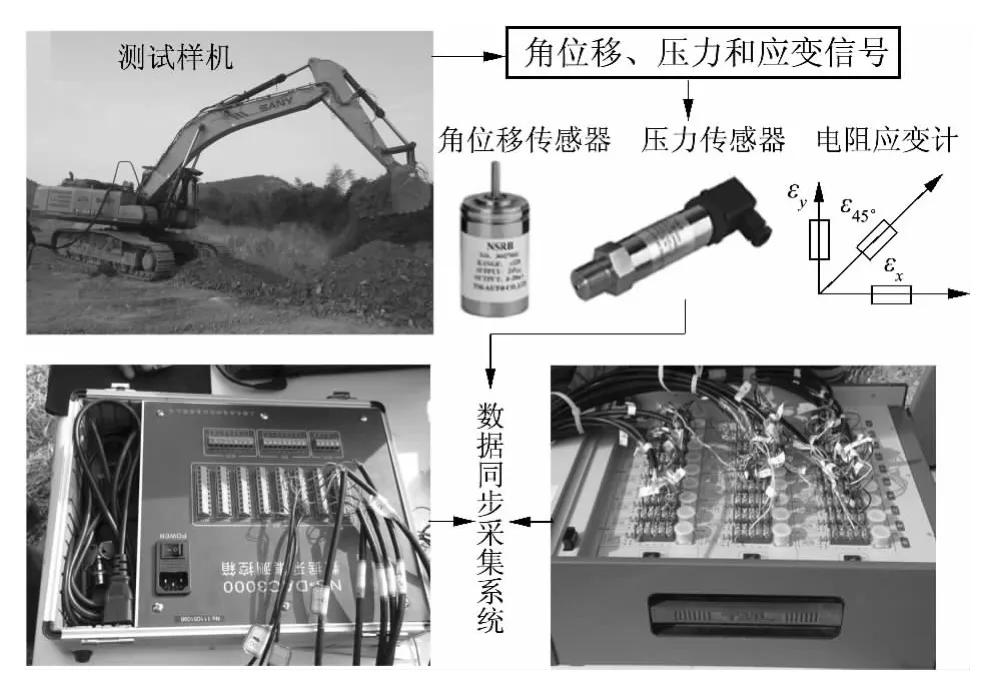
图1 多种数据同步采集测试流程图Fig.1 Synchronous acquisition test flowchart of a variety of data

1.3 测试结果

应变花可实时获取对应测点在0°、90°和45°方向上的应变εx、εy和ε45°，已知材料的弹性模量E和泊松比μ，测点的最大和最小正应力分别为

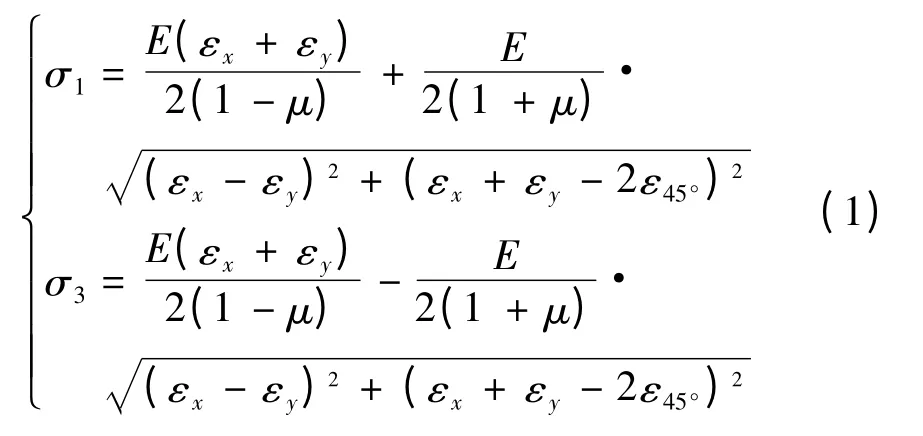
进而，根据第4 强度理论计算出该测点的当量应力σr4:

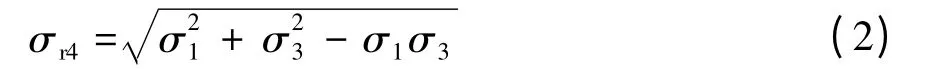
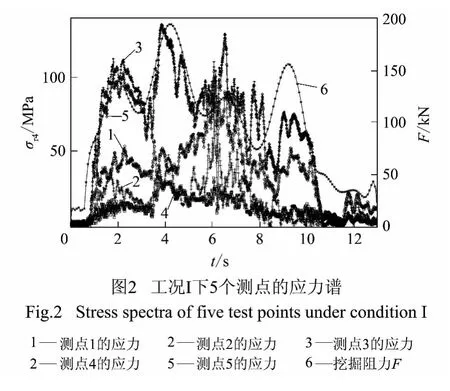
根据测试得到的应变数据和式(1)、(2)，可计算出10 个测点在各种工况下动应力随时间的变化特性.图2 为某一工况I 挖掘过程中测点1 至5 的应力谱.尽管各种工况甚至同一种工况下，不同挖掘过程对应各测点的动应力谱均不相同，但观察所有挖掘过程的动应力计算结果，可得到以下规律:①与理论分析结果相吻合，位于箱形结构横截面角点附近的测点(如测点3 和5)应力较大，而位于箱形结构横截面靠近中间位置的测点(如测点4)应力较小;②动臂承受的应力普遍大于斗杆和铲斗;③所有测点的应力变化规律与挖掘阻力的变化规律一致.

2 动载荷的计算

只有计算出真实准确的载荷才能得到有意义的瞬态分析结果.以往的文献中均以静平衡方法对动载荷进行估算［12-13］，由于大量的简化使得估算结果极不准确，因此，文中基于达朗贝尔动静法原理，对工作装置载荷及铰点力进行动力学求解.当挖掘机不进行回转动作时，工作装置各构件均作平面运动.动臂、斗杆和铲斗的动作均是随其质心移动和绕质心转动的复合动作.图3 给出了动臂、斗杆和铲斗的受力情况.图中，A、B、C、D 分别为动臂与机座、动臂与斗杆、动臂液压缸与动臂、斗杆液压缸与动臂的铰点，H、E、N、G、L 分别为斗杆液压缸与斗杆、铲斗液压缸与斗杆、摇杆与斗杆、铲斗与斗杆、铲斗与连杆的铰点，J 为切削刃中心点，G1、G2、G3分别为动臂、斗杆和铲斗的质心.

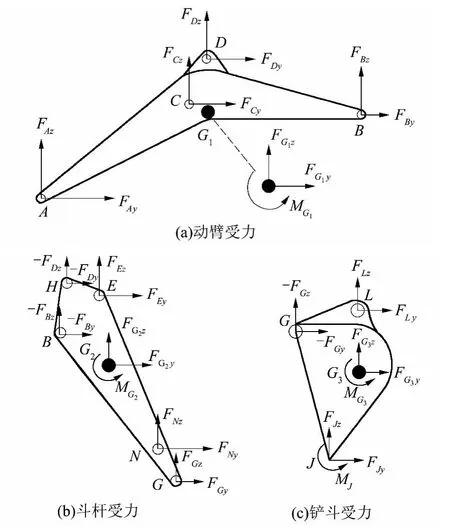
图3 动臂、斗杆和铲斗的受力分析Fig.3 Force analysis of the boom，arm and bucket

根据朗贝尔动静法原理，考虑铰点力、重力和惯性力的共同作用，动臂处于动平衡状态.水平方向合力为0，即

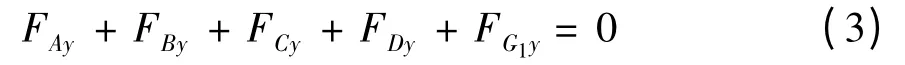
竖直方向合力为0，即

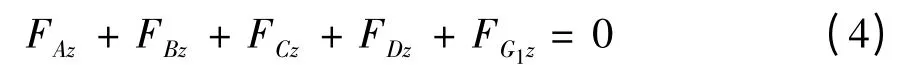
合力矩为0(对质心取力矩)，即

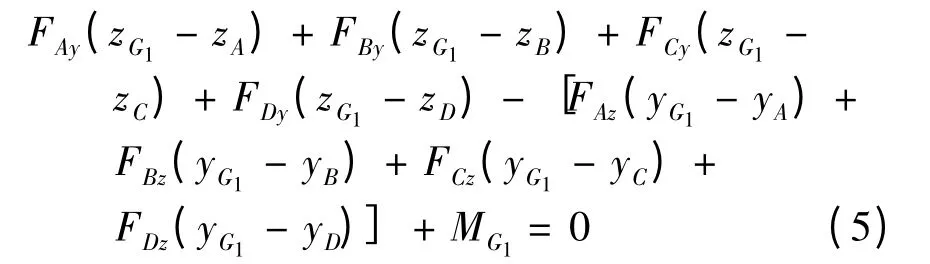
同理，斗杆的动平衡方程为

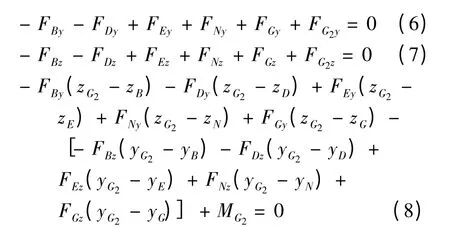
铲斗的动平衡方程为

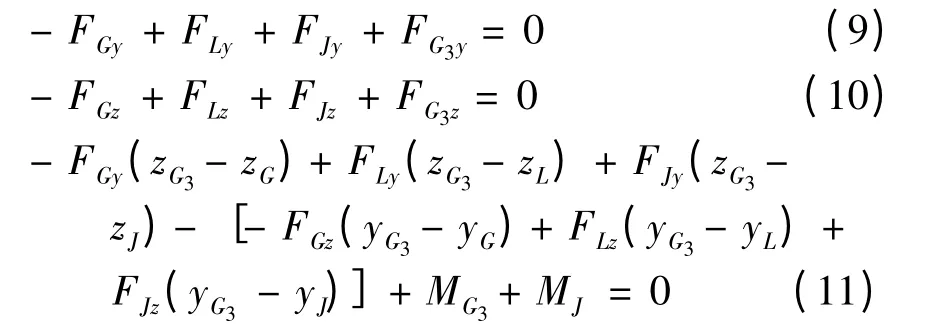
式(3)-(11)中:FXy、FXz分别为铰点(或质心)X在水平方向与竖直方向上所受的力，MX为相应构件在质心X 所受的力矩;yX、zX分别为铰点(或质心)X 在水平方向与竖直方向的坐标;FJy、FJz和MJ分别为将挖掘阻力系向切削刃中心J 合成的水平方向阻力、竖直方向阻力和阻力矩.基于运动学原理，利用角位移传感器采集的3 组角度数据可确定任意时刻工作装置上任意点的空间位置及坐标.将液压缸看作二力杆，利用压力传感器采集的液压缸压强数据，可以得到液压缸施加给工作装置的推力.确定了液压缸的推力，便可以得到与液压缸铰接的工作装置铰点(如铰点C、D、H 和E)的受力.铰点N 和L 虽然不是直接和铲斗液压缸连接，但根据力的传递特性和力矩平衡原理，在已知铲斗液压缸推力的前提下，可以求解出铰点N 和L 的受力.除重力外，工作装置质心还受到惯性力和惯性矩的作用.以动臂为例，动臂质心G1在水平方向上的受力为水平方向的惯性力:

在竖直方向上的受力为竖直方向的惯性力与重力之和:

动臂的惯性矩为

式中，m1为动臂的质量，J1为动臂相对其质心的转动惯量;aG1y和aG1z分别为动臂质心在水平方向和竖直方向上的线加速度，a11为动臂的角加速度，g 为重力加速度.利用角位移传感器采集的3 组角度数据，可以得到工作装置各构件间夹角随时间的变化曲线，对其进行拟合并求导可得到角速度随时间的变化曲线，再次求导便得到各构件间相对角加速度随时间的变化曲线.基于刚体平面运动理论，可得到各构件质心在任意时刻的绝对速度和绝对加速度，从而可计算出aG1y、aG1z和a11，并根据式(12)-(14)计算出动臂质心的受力.同理，可以计算出挖掘过程中任意时刻斗杆和铲斗质心的受力.由以上分析可知，式(3)-(11)中只有铰点A、B、G 的受力和集中于切削刃中心J 的受力不能直接通过测试数据求得，但联立这9 个方程正好可以求解这9 个未知数，从而得到工作装置所有铰点的载荷历程(即常态挖掘过程的载荷谱).图4 给出了动臂各铰点在工况I 挖掘过程中的载荷谱.

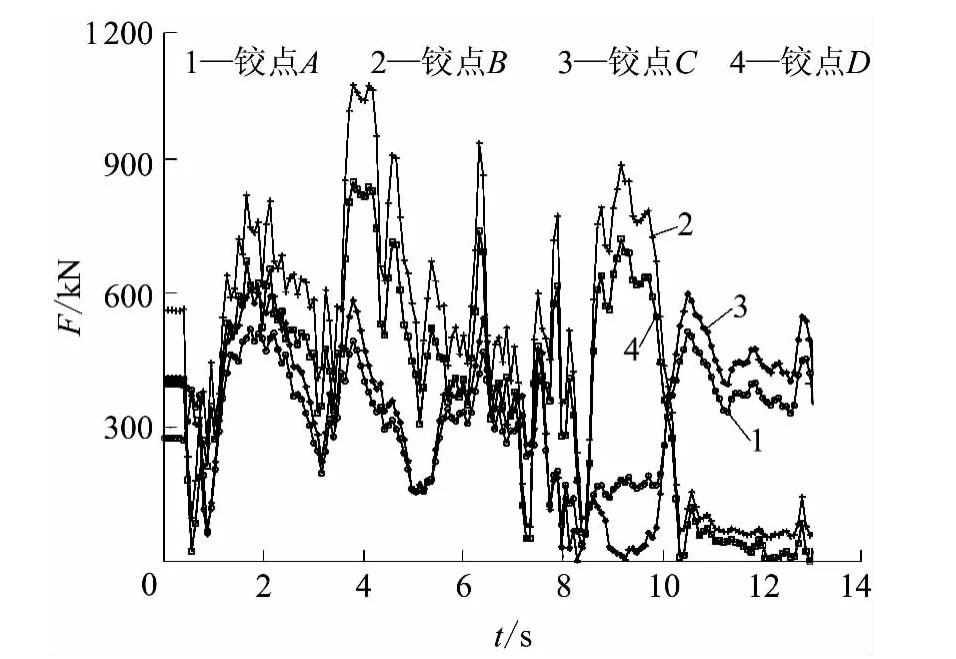
图4 工况I 挖掘过程中动臂各铰点的载荷谱Fig.4 Load spectra of the boom hinge points under digging condition I

3 瞬态分析

应力测试虽然可以准确得到测点的应力值及其变化规律，但不能得到工作装置整体的应力变化规律.为了更加全面地研究挖掘机在常态挖掘过程中的动应力特性，文中采用瞬态分析方法对工作装置构件的整体动应力进行模拟仿真.

3.1 模态分析

为获得模态参数并作为瞬态分析的输入，首先进行模态分析.在Pro/E 中建立动臂与斗杆的三维模型，利用Hypermesh 对其进行网格划分，并定义材料属性和单元属性.将预处理后的模型导入Patran中，并将动臂与斗杆均看成悬臂梁结构，分别对动臂铰点A 和斗杆铰点B 施加全约束.仿真计算得到各阶模态的振形及频率，前5 阶模态频率如表1 所示.

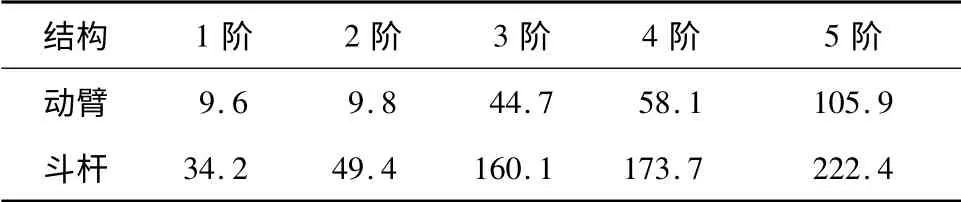
表1 动臂和斗杆的前5 阶模态频率Table 1 The first five-order modal frequencies of the boom and arm Hz

3.2 动应力仿真

将Hypermesh 生成的有限元模型导入Patran 中，并施加约束条件和载荷，其中载荷包括重力载荷和各个铰点上随时间变化的动态载荷.所有载荷需转换到相应的随体坐标系下.然后进行动应力的仿真计算，得到各种不同挖掘工况下动臂和斗杆的动应力随时间的变化规律.文中瞬态仿真应力及危险截面应力均是指第4 强度理论的当量应力.

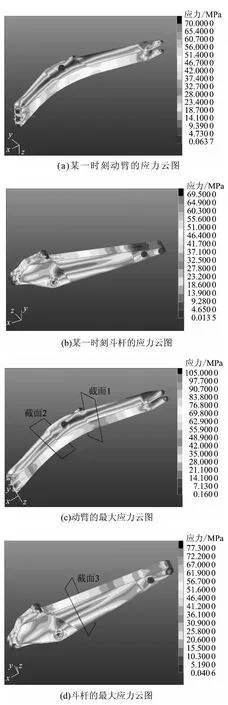
图5 动臂和斗杆的应力云图Fig.5 Stress nephograms of the boom and arm

图5 给出了动臂和斗杆在工况I 挖掘过程中某一时刻的应力云图、最大应力(即整个仿真过程中每个点的最大应力)云图.

4 测试结果与仿真结果分析

4.1 结果对比及误差分析

文中通过测试得到了10 个测点在各种工况下随时间变化的动应力谱，通过瞬态分析得到了动臂和斗杆在各种工况下的整体动应力分布特性.但瞬态分析的有效性还需通过实验结果进行验证.因而，文中提取每个测点在各种工况下的动应力仿真结果，将其与实测结果进行对比.图6 给出了两个测点(位于动臂的测点3 和位于斗杆的测点8)在工况I挖掘过程中的应力实测值与仿真值对比.所有测点在所有挖掘过程中的应力对比结果表明:①应力仿真值与实测值的变化趋势完全相同;②应力实测值一般大于仿真值，尤以测点3 和5 最为明显，其差值接近应力实测值的20%.

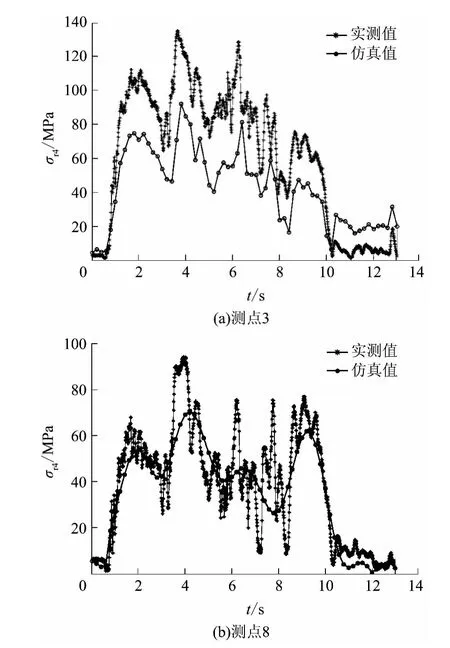
图6 两个测点的应力实测值与仿真值对比Fig.6 Comparison of stress between measured values and simulation values of two test points

分析测试过程和仿真过程之间的差异，发现了应力实测值和仿真值不完全相同的主要原因:①测试过程中存在着一定的偏载和侧向力，但在仿真模型中只施加了正载;②真实的试验样机存在焊缝、自重等影响因素;③实际的应力测点位置和仿真模型中提取的应力测点位置存在一定的误差.因测点3和5 对称分布于动臂弯梁两侧箱形结构的顶点位置，即位于箱形结构的两侧，故受侧向力的影响最大;因同时靠近两条焊缝处于钢板厚度改变位置，故受焊缝引起的应力集中的影响最大.这是测点3 和5 的应力仿真值和实测值差别较大的原因.然而，尽管应力仿真值和实测值存在一定的差别，但两者的变化规律完全吻合.因此，瞬态分析结果是可靠的，能够反映挖掘机在真实挖掘过程中各工作装置的整体动应力变化情况，可以作为确定工作装置动应力分布规律和危险截面的依据.

4.2 动应力分布规律及危险截面的确定

观察所有工况下任意时刻的应力云图和最大应力云图，发现在任何一种工况下，整个动臂和斗杆的应力分布规律几乎完全一致，只有应力大小不同.这说明，当工作装置结构确定后，尽管挖掘工况各异、载荷不同，其动应力的分布规律也具有一致性，最大应力发生的位置也具有一致性.因此，瞬态分析结果可以作为判断工作装置动应力分布规律和危险截面的依据.

根据动臂的最大应力分布规律(见图5(c))可知，动臂应力较大的位置在底板折弯靠前部分、顶板距动臂后端1/4 处和耳板位置.整个动应力呈现渐变规律，以最大应力区域为中心沿动臂长度方向逐渐变小.动臂的危险截面位置如图5(c)中截面1 和2 所示.根据斗杆的最大应力分布规律(见图5(d))可知，斗杆应力较大的区域位于底板中间部位，其危险截面位置如截面3 所示.

5 结论

液压挖掘机长期在恶劣的作业环境中从事着高强度高负荷的工作，结构强度是影响其性能的关键因素.文中通过动态测试和瞬态分析方法研究了工作装置在常态挖掘过程中的动应力特性，避免了静态分析中的载荷及其他误差，所得结果更加符合真实的挖掘过程.基于达朗贝尔动静法原理，文中对挖掘阻力及铰点力进行动力学求解，得到各个铰点对应的真实载荷，从根本上保证了瞬态分析的正确性.应力的瞬态分析与测试结果表明:尽管仿真曲线和测试曲线不完全重合，但两者的变化规律一致;瞬态分析结果能够反映挖掘机常态挖掘过程中工作装置的整体动应力特性，可以作为判断工作装置动应力分布规律和危险截面的依据.本研究为挖掘机工作装置载荷计算和结构强度的设计评价提供了一种可靠方法.

［1］Patel Bhaveshkumar P，Prajapati J M.Soil-tool interaction as a review for digging operation of mini hydraulic excavator［J］.International Journal of Engineering Science and Technology，2011，3(2):894-901.

［2］Patel Bhaveshkumar P，Prajapati J M.A review on kinematics of hydraulic excavator’s backhoe attachment［J］.International Journal of Engineering Science and Technology，2011，3(3):1990-1997.

［3］Hoan Le Quang，Jeong Chan Se，Kim Hack Sun，et al.Study on modeling and control of excavator ［C］∥Proceedings of the 28th International Symposium on Automation and Robotics in Construction.Seoul:IIT Madras，2011:969-974.

［4］Patel Bhaveshkumar P，Prajapati J M.A review on FEA and optimization of backhoe attachment in hydraulic excavator［J］.International Journal of Engineering and Technology，2011，3(5):505-511.

［5］陈进，吴俊，李维波，等.大型液压正铲挖掘机工作装置有限元分析及应力测试［J］.中国工程机械学报，2007，5(2):198-203.Chen Jin，Wu Jun，Li Wei-bo，et al.Finite element analysis and stress testing for manipulator in large sized face shovel hydraulic excavator［J］.Chinese Journal of Construction Machinery，2007，5(2):198-203.

［6］周宏兵，王慧科，过新华，等.基于MATLAB 和ANSYS的挖掘机工作装置结构静强度分析［J］.广西大学学报:自然科学版，2009，34(6):774-779.Zhou Hong-bing，Wang Hui-ke，Guo Xin-hua，et al.Static strength analysis of working device of hydraulic excavator based on MATLAB and ANSYS ［J］.Journal of Guangxi University:Nature Science Edition，2009，34(6):774-779.

［7］杜文靖，崔国华，刘小光，等.液压挖掘机工作装置整体集成有限元分析［J］.农业机械学报，2007，38(10):19-23.Du Wen-Jing，Cui Guo-hua，Liu Xiao-guang，et al.Integration finite element analysis on whole working equipment of hydraulic excavator［J］.Transactions of the Chinese Society for Agricultural Machinery，2007，38(10):19-23.

［8］Cui Guohua，Zhang Yanwei.Integrated finite element analysis and experimental validation of an excavator working equipment［C］∥Proceedings of 2009 International Conference on Information Engineering and Computer Science.Wuhan:IEEE，2009:1-4.

［9］Tian Long，Zhang Wei，Wang Hai-bo.Study on finite element method of power working device of hydraulic excavator［C］∥Proceedings of the 2011 International Conference on Electronic ＆ Mechanical Engineering and information Technology.Harbin:IEEE，2011:4216-4219.

［10］Bošnjak Srdan M，Petkovic Zoran D，Atanasovska Ivana D，et al.Bucket chain excavator:failure analysis and redesign of the counterweight boom supporting truss columns［J］.Engineering Failure Analysis，2013，32:322-333.

［11］程珩，百瑞.挖掘机工作装置疲劳寿命分析［J］.振动、测试与诊断，2011，31(4):512-516.Cheng Hang，Bai Rui.The fatigue life analysis of excavator working device ［J］.Journal of Vibration，Measurement ＆ Diagnosis，2011，31(4):512-516.

［12］张卫国，权龙，程珩，等.基于真实载荷的挖掘机工作装置瞬态动力学分析［J］.机械工程学报，2011，47(12):144-149.Zhang Wei-guo，Quan Long，Cheng Hang，et al.Transient dynamic analysis on working device of excavator based on practical load ［J］.Journal of Mechanical Engineering，2011，47(12):144-149.

［13］张卫国，权龙，程珩，等.真实载荷驱动下挖掘机工作装置疲劳寿命研究［J］.农业机械学报，2011，42(5):35-38.Zhang Wei-guo，Quan Long，Cheng Hang，et al.Fatigue analysis on working device of excavator driven by practical load［J］.Transactions of the Chinese Society for Agricultural Machinery，2011，42(5):35-38.

［14］杨为，邱清盈，胡建军.液压挖掘机工作装置动应变的实验研究［J］.工程机械，2004(11):15-19.Yang Wei，Qiu Qing-ying，Hu Jian-jun.Experimental study of dynamic stress of the hydraulic excavator working device ［J］.Construction Machinery and Equipment，2004(11):15-19.

［15］Solazzi Luigi.Design of aluminium boom and arm for an excavator［J］.Journal of Terramechanics，2010，47(4):201-207.