多齿啮合行星机构的传动精度分析*

林超 蔡志钦

(重庆大学 机械传动国家重点实验室，重庆 400030)

在工业应用中，传统行星齿轮机构已经被广泛采用［1］，但在一些特殊的场合(如五轴联动机床加工的一些军工产品、飞机舱门系统)，对产品本身的传动精度和定位精度要求很高.目前已有不少对行星齿轮精密传动方面的研究.文献［2-4］认为加工误差和安装误差是影响行星齿轮系统传动精度的主要因素，其中偏心误差影响最大，但未深入研究其影响的程度.文献［5-6］中考虑齿轮基圆的偏心误差，通过建立的几何模型讨论了齿轮副传动误差随齿轮转角而变化的规律，但此方法仅针对圆柱齿轮副，未对行星齿轮机构进行研究.文献［7-8］探讨了齿轮的装配误差和偏心误差对齿轮副传动精度及均载特性的影响，但未考虑弹性变形和负载对传动精度的影响.文献［9-11］中对行星齿轮系统传动误差的预测理论及方法进行了研究.文献［12-14］中利用概率统计法对齿轮机构的回差进行了分析，但通过此方法无法得到传动误差的变化过程.文献［15］中探讨了圆柱齿轮副的回差控制与补偿，为进一步提高齿轮的传动精度提供了新的思路.

为此，文中设计了一种可以满足高精密传动的新型传动机构——多齿啮合行星机构，考虑了偏心误差、行星齿轮的相位角、弹性变形与负载对机构传动精度的影响，建立了多齿啮合行星机构的传动精度模型，得到了机构的传动精度随着输入转角变化的规律，并与传统行星机构进行对比分析.

1 多齿啮合机构的设计

与传统二级NGW(2K-H 负号机构)行星机构(以下简称传统机构)相比，文中设计的多齿啮合行星机构(以下简称多齿啮合机构，见图1)由电机驱动太阳轮1，通过定轴轮2 将动力由内外齿圈3-3'输出，内外齿圈3-3'直接驱动第2 级行星机构，最后由行星架6 输出，实现多齿啮合机构的基本传动.

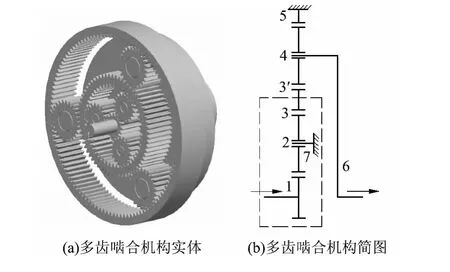
图1 多齿啮合机构Fig.1 Multi-tooth meshing planetary mechanism

2 机构传动精度的数学模型

一般而言，传动误差包括输出转角误差和回差两部分.对齿轮副而言，传动误差主要由安装偏心误差和弹性变形引起，因此文中在建模时考虑了安装偏心误差和弹性变形对机构传动精度的影响.

2.1 输出转角误差数学模型

以多齿啮合机构为例，建立其局部传动精度数学模型，如图2 所示.现做如下假设:①齿轮的安装误差综合成安装偏心误差;②啮合副间无变形;③回转中心共线时的传动比为理论传动比.

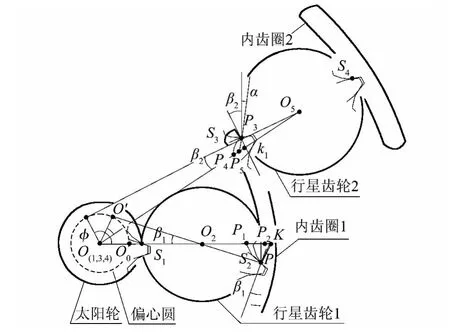
图2 多齿啮合行星机构的局部啮合示意图Fig.2 Schematic diagram of local meshing of multi-tooth meshing planetary mechanism

图2 中，φn(n=1，2)为输入转角，Oj(j= 1，2，…，5)为基圆中心，α 为啮合角，βn为偏心角，Pn为随机啮合点，Sn为啮合点.设P2为回转中心共线时两齿轮的啮合点，P 为任意啮合点.过P 做直线PK ∥O1O'.根据齿轮啮合原理的相关知识可知，齿轮副的传动比误差为

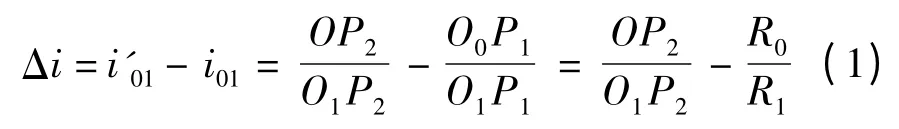
式中，i'01为实际传动比，i01为理论传动比，R0、R1、O0、O1分别为内齿圈和外齿轮的分度圆半径及中心.

由于式(1)建立在无变形的基础上，与实际工况有所区别.因此，文中结合实际情况考虑弹性变形与负载对传动精度的影响.

齿轮在任一受载位置时，受载点沿啮合线方向的变形量为［16］

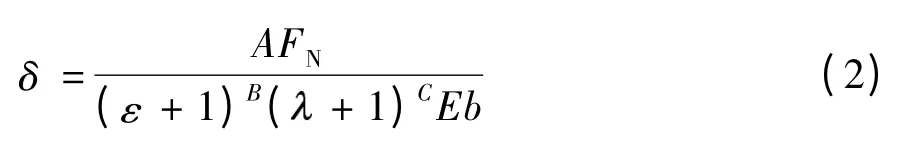
式中，FN为齿面上的法向总载荷，ε为移距系数，为加载点的位置，1.22，z 为齿轮齿数，E 为弹性模量，b 为齿轮齿宽.

受载点沿啮合线方向的变形量对齿轮副之间传动误差的影响最大.因此，取该变形量为弹性变形所引起的传动误差.

综合考虑上述几种影响因子，则机构的传动比inm误差为

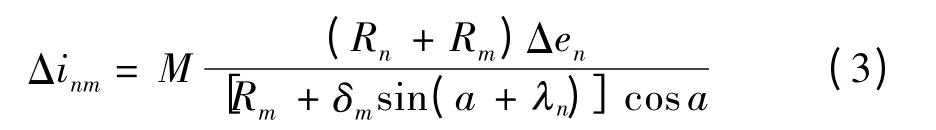
式中:Δen为偏心误差;Rm和Rn分别为主动轮和从动轮的分度圆半径;n=1，2，3'，4;m=2，3，4，5;n=Δe 为偏心误差;a 为压力角;φn为输入转角;N 为行星轮个数;p=1，2，3.

由传动比误差可求得多齿啮合机构的输出转角误差为

式中，

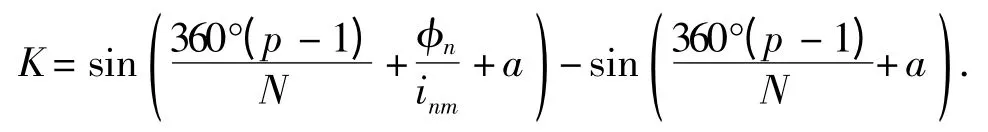
由式(4)可知，多齿啮合机构的输出转角误差矩阵为

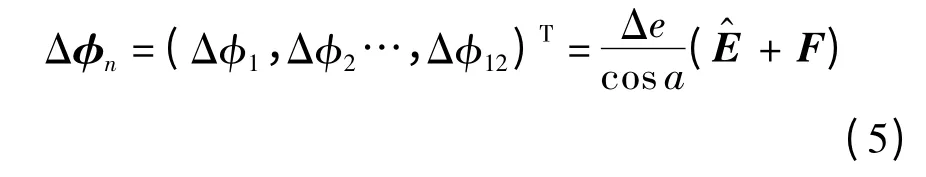
式中，

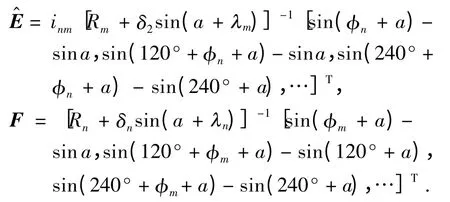
同理，可得到传统行星机构的输出转角误差矩阵.

2.2 回差数学模型

当综合考虑偏心误差、相位角、弹性变形和负载对传动精度的影响时，机构的回差为

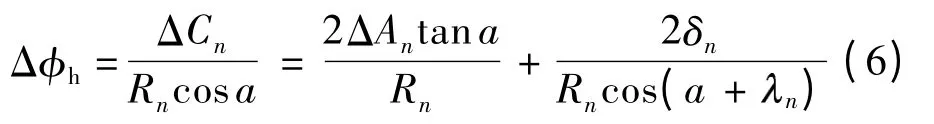
由式(6)可知，多齿啮合机构的回差矩阵为

式中，

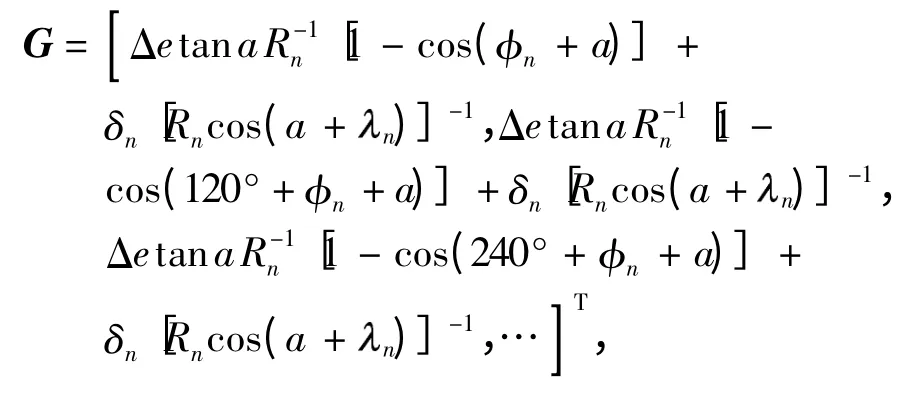
同理，可得到传统行星机构的回差矩阵.

3 机构传动精度仿真分析

选取两机构的功率为5 kW，传动比为20，输入转速为600 r/min，负载为100 kg，齿轮精度等级均为6 级.机构的基本参数如表1 所示.

通过传动机构的几何形状参数，结合转角误差、回差的运动学方程，将传统机构与多齿啮合机构分别分解为4 个啮合副，得到机构的啮合副综合转角误差与回差(见图3)，只取输出转角一周内的转角误差与回差.通过将每一级的传动误差相互叠加，最终可得到机构的输出转角误差和回差.

表1 机构的基本参数Table 1 Basic parameters of the mechanism

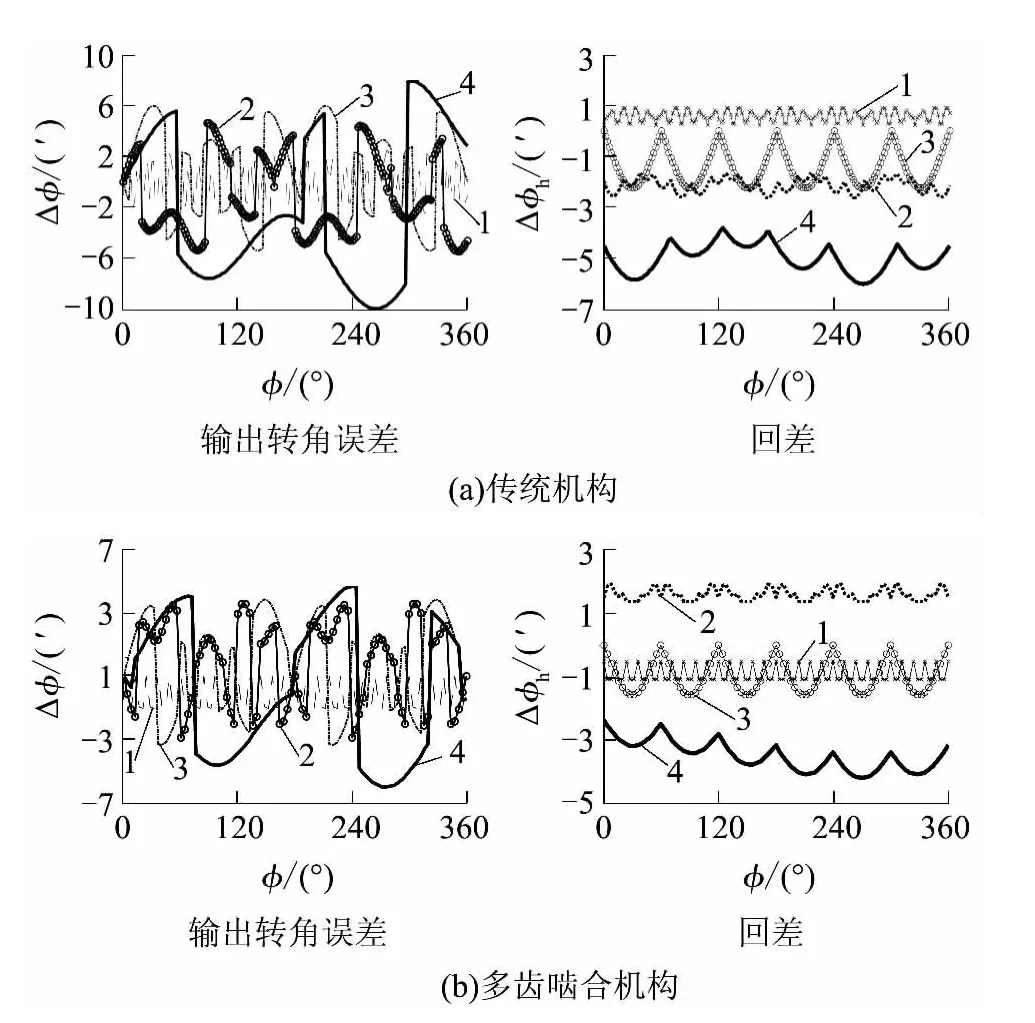
图3 两种机构的输出转角误差与回差比较Fig.3 Comparison of output angle error and rotational error between two mechanisms

为便于对多齿啮合机构和传统机构的输出转角误差和回差进行对比分析，文中做如下假设:①两种机构的传动比及偏心误差相同;②两种机构的径向尺寸相同;③两种机构最小齿轮(第1 级太阳轮)的接触强度和弯曲强度均满足强度条件.将啮合副的传动误差(转角误差和回差)进行叠加，可得到多齿啮合机构和传统机构的传动误差，结果如图4 所示，其中转角误差是衡量机构传动精度的重要指标，回差是反映机构传动精度的标准.

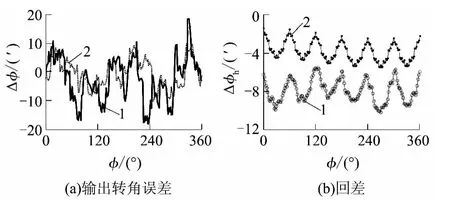
图4 两种机构的输出参数对比Fig.4 Comparison of output parameters between two mechanisms

由图4 可知:多齿啮合机构的最大转角误差为28.21'，比传统机构的最大转角误差34.83'降低了19.0%;多齿啮合机构的最大回差为3.57'，比传统机构的最大回差4.42'降低了19.2%.这表明，多齿啮合机构的传动精度要高于传统机构，且误差的波动范围要小于传统机构.这适合一些对传动精度有严格要求的场合.

4 综合分析

根据表1 参数对两种机构分别建立仿真模型并进行分析，同时对机构进行简化实验分析.

4.1 仿真分析

在空载情况下，输入转速为600 r/min，仿真时间为3 min，仿真步数为160;给输入轴施加一个固定转速(为600 r/min)的驱动，仿真时间为3 min，仿真步数为160.分别得到两种机构在正反转情况下的输出转角误差和回差，结果如图5 所示.

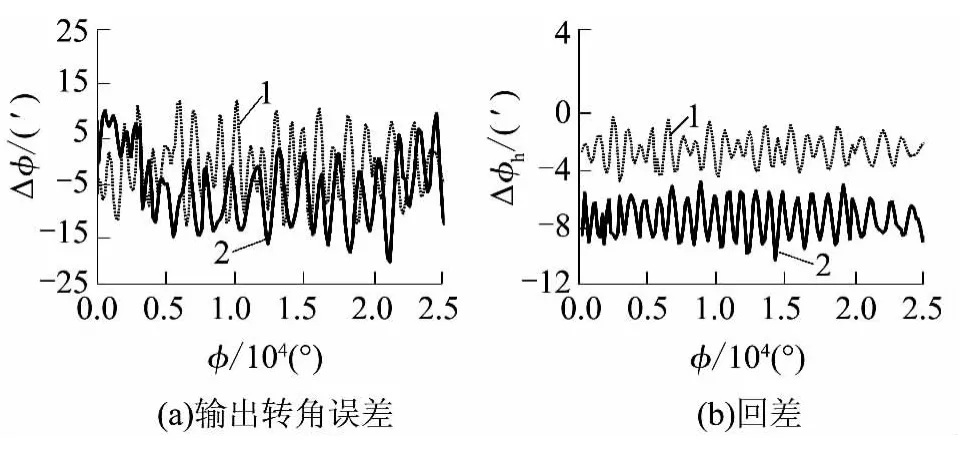
图5 传动误差的仿真结果对比Fig.5 Comparison of simulation results of transmission errors

由仿真结果可知，多齿啮合机构的最大转角误差为29.22'，最大回差为4.18'，比传统机构的最大转角误差35.42'和最大回差5.12'分别降低了17.5%、18.4%，这说明多齿啮合机构的传动精度高于传统行星机构.

4.2 实验验证

考虑到多齿啮合机构和传统行星机构的第2 级传动基本相同，文中对这两种机构进行简化实验，仅研究第1 级输出所引起的传动误差.在机械封闭式齿轮传动实验台上完成该实验台的安装，如图6 所示.行星减速器实验系统简图与实验装置简图见图7，实验装置的基本参数如下:za=18，zb=27，zc=72，z1=76，z2=148，模数为2 和3mm.

图6 实验设备Fig.6 Experimental equipment

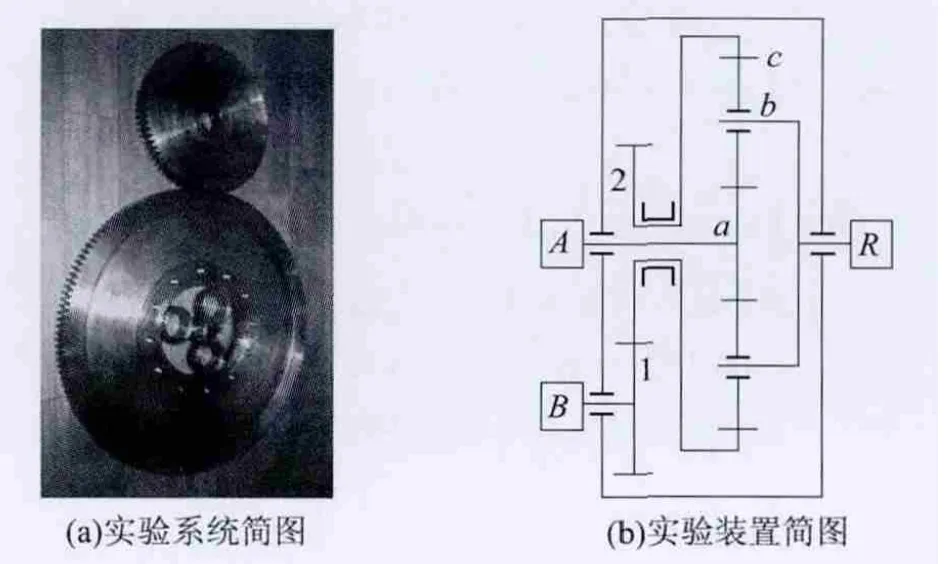
图7 行星减速器装置Fig.7 Planetary reducer device

分别固定轴B 和R，当输入扭矩由50 Nm 增加到65 Nm 恒定、转速由600 r/min 分阶上升到900 r/min正转(+)，或输入扭矩由65 Nm 减少到50 Nm恒定、转速由900 r/min 分阶下降到600 r/min反转(－)时，轴A、R 和B 的输出转速ω 与时间t 的关系如图8 所示.

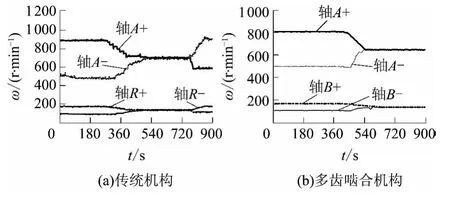
图8 两种机构的第1 级输出转速Fig.8 The first-level output angel of two mechanisms

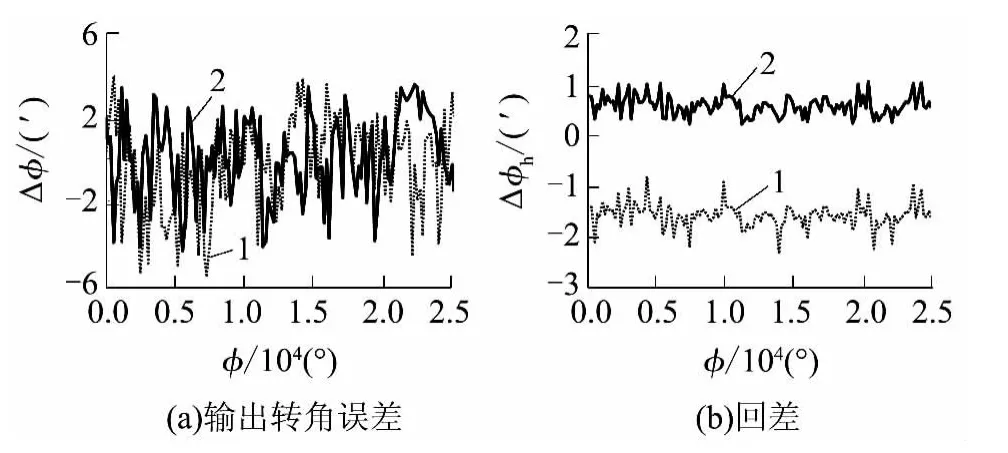
图9 传动误差的实验结果对比Fig.9 Comparison of experimental results of transmission errors

将两种工况下正反转转速重合的部分做进一步处理，得到两种机构的输出转角误差和回差(见图9).

由实验结果可知，多齿啮合机构第1 级行星机构输出的最大转角误差为8.03'，最大回差为0.95'，比传统机构的最大转角误差9.21'和最大回差1.25'分别降低了12.8%、24.0%.这说明多齿啮合机构的第1 级行星机构的传动精度高于传统行星机构.

4.3 综合对比分析

两种机构的数学模型计算结果和通过ADAMS仿真所得到的结果如图10 所示.由图可知，数学建模和ADAMS 仿真所得到的输出转角误差、回差曲线变化趋势趋于一致，但仍然存在一定的误差，这主要是由机构在运动过程中齿面之间的冲击和振动造成的.

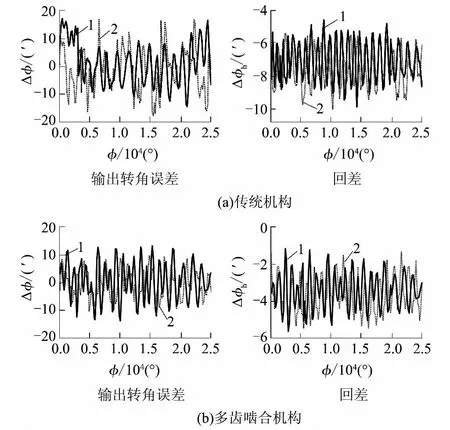
图10 两种机构的ADAMS 仿真结果与模型计算结果对比Fig.10 Comparison of ADAMS simulation results with model calculation results between two mechanisms

对传统机构而言，最大输出转角误差、最大回差的仿真值与计算值的相对误差分别为1.6%、13.7%;对多齿啮合机构而言，最大输出转角误差、最大回差的仿真值与计算值的相对误差分别为3.4%、15.2%.

第1 级行星机构的实验结果和数学模型计算结果如图11 所示.

由图可见，数学建模和实验所得到的第1 级行星机构的输出转角误差、回差曲线变化趋势趋于一致，但仍然存在一定的误差，这主要是由实验过程中存在的安装误差、制造误差及操作环境等造成的.

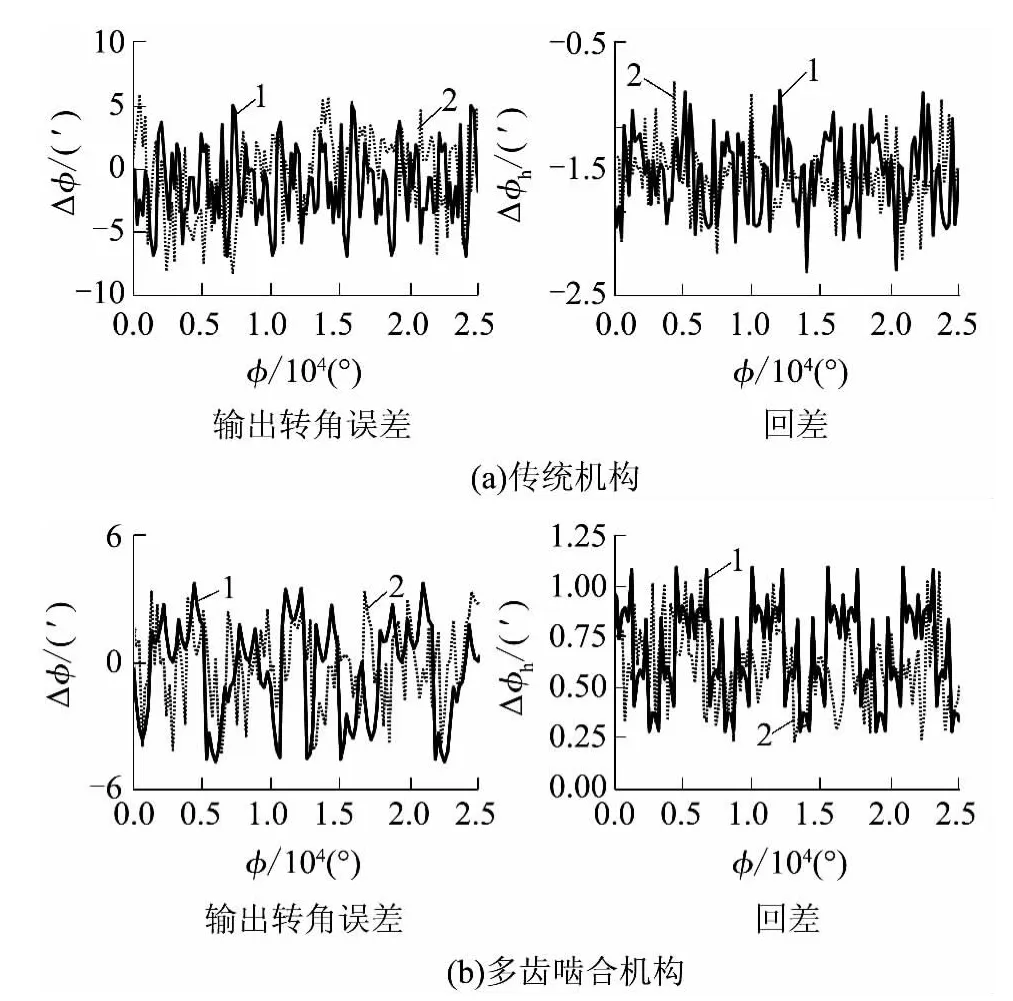
图11 两种机构的第1 级行星机构的模型计算结果与实验结果对比Fig.11 Comparison of model calculation results with experimental results between the first-level planetary mechanisms of two mechanisms

对传统机构的第1 级行星机构而言，通过数学模型计算得到的最大输出转角误差为8.26'、最大回差为1.11'，与实验结果的相对误差分别为11.2%和11.1%.对多齿啮合机构的第1 级行星机构而言，通过数学模型计算得到的最大输出转角误差为7.51'、最大回差为0.84'，与实验结果的相对误差分别为6.3%和10.5%.

5 结论

文中考虑偏心误差、行星齿轮的相位角、弹性变形与负载对机构传动精度的影响，首先对多齿啮合机构进行传动精度分析，结果表明:多齿啮合机构的传动精度要高于传统机构;由于多齿啮合机构的输出转角误差比传统机构小，因此多齿啮合机构的传动更加平稳，在对传动稳定性有严格要求的场合具有更明显的优势.然后对多齿啮合机构和传统机构的ADAMS 运动学仿真与数学模型计算进行对比分析，结果表明，文中所建立的数学模型基本上是正确的，但仍然存在一定的误差，这是由机构在运动过程中齿面之间的冲击和振动造成的.最后对机构进行简化实验研究，结果表明，多齿啮合机构的第1 级行星机构的输入转速要比传统机构稳定，由于多齿啮合机构和传统机构的第1 级机构基本相同，因此，多齿啮合机构的输出稳定性与传动误差要高于传统机构，这表明简化实验结果与数学模型计算结果和仿真实验结果一致.

［1］饶振纲.行星齿轮传动设计［M］.北京:化学工业出版社，2003.

［2］Li S T.Effects of machining errors and tooth modification on loading capacity，load-sharing ratio and transmission on error of a pair of spur gears［J］.Mechanism and Machine Theory，2007，42(6):698-726.

［3］Nagahata D，Hendricx W，Anthonis J，et al.Reducing gear whine of a valtra continous variable transmission［C］∥Proceedings of the VDI Berichte Conference on Agricultural Engineering.Hannover:VDI-MEG，2009:113-122.

［4］张铁，谢存禧.影响短幅摆线行星减速器回差的因素［J］.华南理工大学学报:自然科学版，1999，27(2):23-27.Zhang Tie，Xie Cun-xi.Influence factors of reverse error in short cycloidal planet reductor ［J］.Journal of South China University of Technology:Natural Science Edition，1999，27(2):23-27.

［5］GeorgeW.Michalec.Precision gearing:theory and practice［M］.New York:John Wiley ＆ Sons，1966.

［6］吴慈生.齿轮偏心误差所引起的传动误差［J］.南京工学院学报，1982，25(4):133-145.Wu Ci-sheng.The turning angel error from gears eccentric error［J］.Journal of Nanjing Academy of Engineering，1982，25(4):133-145.

［7］何恩义，陈扬枝.装配误差对空间曲线啮合齿轮传动精度的影响［J］.华南理工大学学报:自然科学版，2012，40(12):24-29.He En-yi，Chen Yang-zhi.Effects of assembly errors on transmission precision of space curve meshing wheel［J］.Journal of South China University of Technology:Natural Science Edition，2012，40(12):24-29.

［8］朱增宝，朱如鹏.偏心与安装误差对封闭差动人字齿轮传动系统静力学均载特性的影响［J］.华南理工大学学报:自然科学版，2011，39(8):19-25.Zhu Zeng-bao，Zhu Ru-peng.Impacts of eccentric and installation errors on static load sharing behaviors of encased differential herringbone train［J］.Journal of South China University of Technology:Natural Science Edition，2011，39(8):19-25.

［9］王朝兵，陈小安.误差随机性对行星齿轮系传动精度的影响特性［J］.重庆大学学报:自然科学版，2012，35(9):41-47.Wang Chao-bing，Chen Xiao-an.Influence of error's randomness on precision of planetary gear ［J］.Journal of Chongqing University:Natural Science Edition，2012，35(9):41-47.

［10］Palmer D，Pears J，Smith A，et al.Design consideration of planetary System for transmission error prediction［C］∥Proceedings of the International Conference on Mechanical Transmission.Chongqing:Science Press，2006:800-889.

［11］Pears J，Smith A，Curtis S.A software tool for the prediction of planetary gear transmission error［C］∥Proceedings of International Conference on Gears.Garching:VDI Beriche，2005:357-372.

［12］解晓辉.NGW 行星齿轮减速器回差分析［D］.郑州:郑州机械研究所，2004.

［13］叶期传，徐辅仁.用概率统计法计算齿轮机构回差［J］.机电设备，2003(1):16-19.Ye Qi-chuan，Xu Fu-ren.Calculated the backlash of gear mechanism by using probabilty and statistics［J］.Electromechanical Equipment，2003(1):16-19.

［14］李聚波，贺红霞.齿轮传动精度的分析和计算［J］.煤矿机械，2006，27(7):18-20.Li Ju-bo，He Hong-xia.Analysis and calculation of precision of gear transmission ［J］.Coal Mine Machinery，2006，27(7):18-20.

［15］李俊阳，王家序.渐开线内啮合圆柱齿轮副的回差控制与补偿［J］.重庆大学学报:自然科学版，2012，35(7):43-48.Li Jun-yang，Wang Jia-xu.Backlash control and compensation for internal meshing involute spur gears［J］.Journal of Chongqing University:Natural Science Edition，2012，35(7):43-48.

［16］赵东升，汪中厚.基于CAE 的渐开线直齿圆柱齿轮的刚度可靠性研究［J］.现代制造工程，2010(6):44-46.Zhao Dong-sheng，Wang Zhong-hou.Exploration of the reliability of the stiffness analysis of the involutes gear based on CAE［J］.Modern Manufacturing Engineering，2010(6):44-46.