单摆周期公式的综合修正

黄兆梁

(常州工学院光电工程学院，江苏常州213002)

单摆周期公式的综合修正

黄兆梁

(常州工学院光电工程学院，江苏常州213002)

从Lagrange函数出发导出单摆振动的运动方程，得到单摆周期的各主要修正项，包括复摆修正、空气浮力修正、阻尼力修正和大摆幅修正等，修正项均保留到二级或以上小量，更正了以往单摆修正公式中的一些失误，给出了在大摆幅情况下的单摆周期的高精度近似公式，从而使单摆周期的计算可以更为准确可靠。

单摆；周期；非线性；大摆幅；修正

O313.1

A

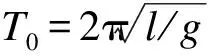
1 无阻尼小摆幅单摆周期公式推导

考虑到实际情况，将单摆视为一质量为m、半径为r的小球被质量为μ的不可伸长的均质细线悬挂于定点o，小球质心到悬点的距离为l，细线与铅垂线的夹角为θ。考虑到复摆修正时，单摆的动能为

(1)

设小球材料的密度为ρ，质量为m，空气密度为ρ0，考虑到小球所受空气浮力修正和摆幅修正，单摆的势能为

(2)

该系统的Lagrange函数为

(3)

考虑到非保守的空气阻尼力与速度成正比，可表示为

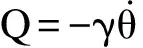
(4)

根据拉格朗日方程

(5)

可得：

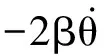
(6)

即：

(7)

(8)

在不计阻尼(即β=0)以及小振幅的情况下，显然有sinθ≈θ，因此

(9)

(10)

式(10)精度较高，也可采用式(11)计算，但精度稍差。

(11)

这里推导出的公式与部分文献略有不同[1-3]，有些文献推导中忽略了应保留的二级小量(包括2个一阶小量的乘积)，导致二级小量的表达式不够准确。由于细线波动影响相对较小可予以忽略，因此在上述推导过程中没有考虑细线中的波动。

如果已确知当地的重力加速度g，则可根据式(10)求得单摆周期T0为：

(12)

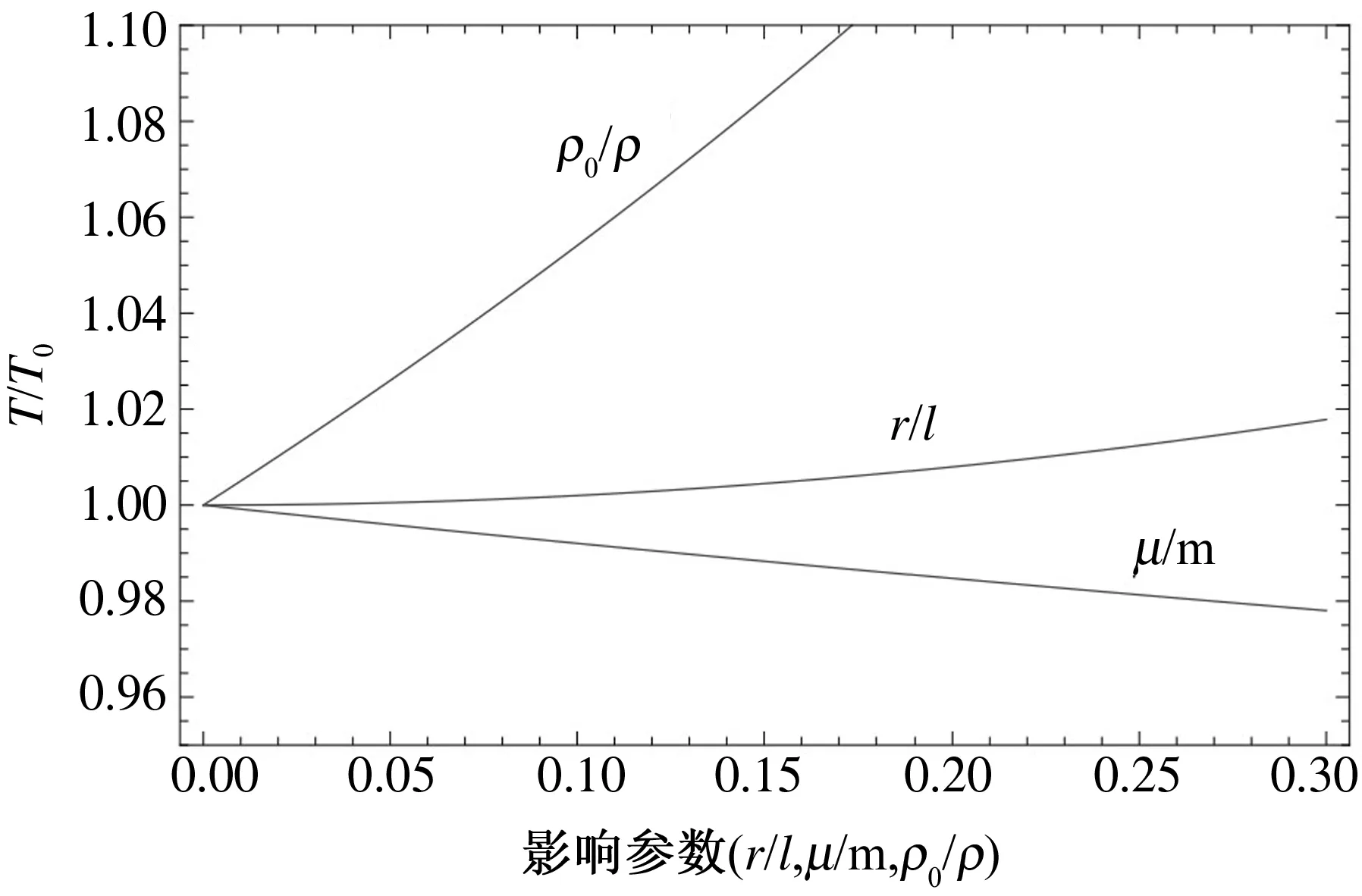
图1 各参数对单摆振动周期的影响

2 单摆小摆幅阻尼修正

上述讨论中假设阻尼可以忽略不计，但实际上由于空气阻尼等的存在，使单摆的振荡会逐渐衰减直至停止。

根据式(6)与式(9)，以及小摆幅条件sinθ≈θ，式(7)可近似为

(13)

(14)

这里可分为3种情况：

1)β>ω0，称为过阻尼，单摆摆幅较缓慢地持续衰减到平衡状态；

2)β=ω0，临界阻尼，单摆摆幅较快衰减到平衡状态，呈振荡的临界状态；

3)β<ω0，欠阻尼，单摆呈周期性振荡并持续衰减到平衡状态。

其单摆的3种振荡情况如图2所示。

图2 单摆的3种阻尼振荡情况

在欠阻尼情况下，式(14)也可以表达为

(15)

单摆在空气中的摆动由于阻尼力很小，因此均为欠阻尼振荡情况，其实际振荡频率将会比无阻尼情况略小，振荡圆频率ω为

(16)

这里的β可通过摆幅衰减情况来测定。设初始摆幅为θ0，摆动m次后摆幅衰减为θm，则

(17)

由此可推得振荡圆频率ω为

(18)

若摆动n次后摆幅衰减为一半，则

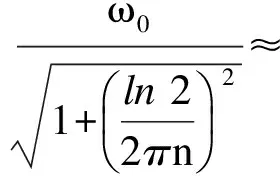
(19)

随着摆幅半衰次数n的增加，其频率也将越接近无阻尼振荡频率，如，半衰摆动次数为10次，则频率为无阻尼时的0.999 94倍，周期将为无阻尼时的1.000 06倍，频率仅减小了6×10-5，或相当于周期增大了6×10-5，显然，这时阻尼对振动频率或周期的影响微乎其微，如图3所示。

图3 振荡频率与摆幅半衰次数n的关系

阻尼对摆动周期的影响为

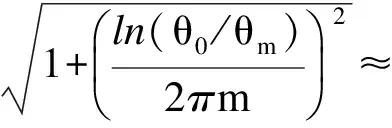
(20)

依据微小误差原理，阻尼的影响修正只需在无阻尼的结果中添加阻尼项修正即可。

3 无阻尼大摆幅振荡的修正

上述讨论是基于小摆幅假设，现考虑无阻尼大摆幅振荡，这时式(13)需改为

(21)

求解上述非线性微分方程可解得其振动周期[8]的精确解为

(22)

随着单摆摆幅θ0的增大，周期T1也将随之增大。摆幅对周期的影响如图4所示，随着摆角的增大其摆动周期也越来越长，并呈加速趋势。图4中T2(1)表示单摆周期的幂级数T2的一级近似式，T2(2)表示T2的二级近似式。

图4 摆幅对单摆周期的影响

从图4可以看出,单摆摆幅与摆动周期的关系。在不需要非常精确的情况下，摆动周期常用近似解来表示。其中单摆周期的幂级数近似解T2的五级修正公式[8]为

(23)

无论是用精确的式(22)或是近似的式(23)求解都不太方便。为了既有高精度同时公式又简洁，许多文献都对椭圆函数的积分近似进行了研究[3-10]，并获得了许多较好的近似公式，如文献[5]给出

(24)

文献[6]提供了一个精度较好的拟合公式

(25)文献[7]给出了其推荐的具有较高精度的近似式

(26)

文献[9]给出了通过三次函数拟合得到的公式

(27)同时也给出了一个其认为具有较高精度的修正公式

(28)

本文在式(24)基础上进一步拟合优化，得到：

(29)

式(29)是具有更高精度的修正公式。

对上述8个周期计算公式计算其周期与理想单摆周期的比值，其随最大摆角的变化情况如表1、表2所示。

为更清晰地显示各计算式的误差情况，以精确的T1作为比较基准，计算在(0，π/2)弧度即(0°，90°)内的误差(Ti-T1)/T0，并绘制出各公式的误差曲线，如T2(5)的误差(T2(5)-T1)/T0，以此类推。其中T2(5)、T3、T5、T6、T7的误差曲线如图5所示；T2(5),T3,T4、T8精度较高，其误差曲线如图6所示。

显然这里T8在(-π/2,π/2)或(-90°，90°)范围内，误差小于1.7×10-6，在所有参与比较的近似公式中精度最高，T2(5)次之，T3第三，T4第四，T5第五，T6第六，而T7的精度最低。其中T8不仅精度最高，且函数形式也相当简洁，因此以T8作为单摆大摆幅周期的近似计算公式具有明显优势。

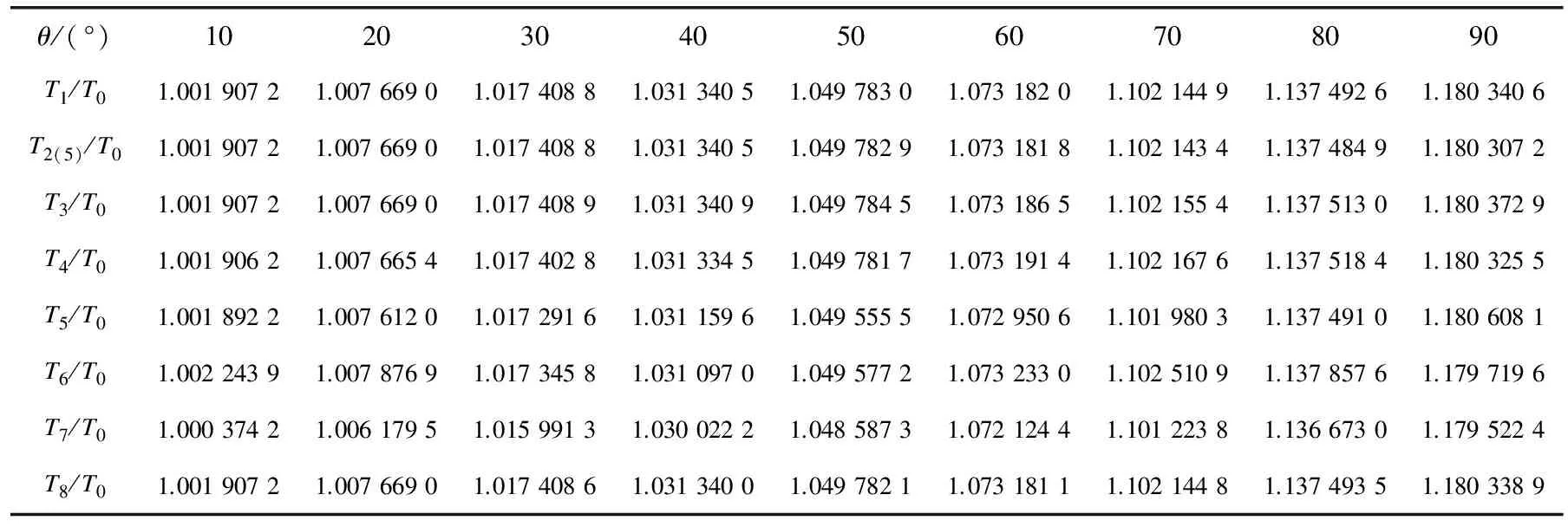
表1 对应摆角θ下精确周期T1以及周期的各近似表达式Ti与理想单摆周期的比值Ti/T0

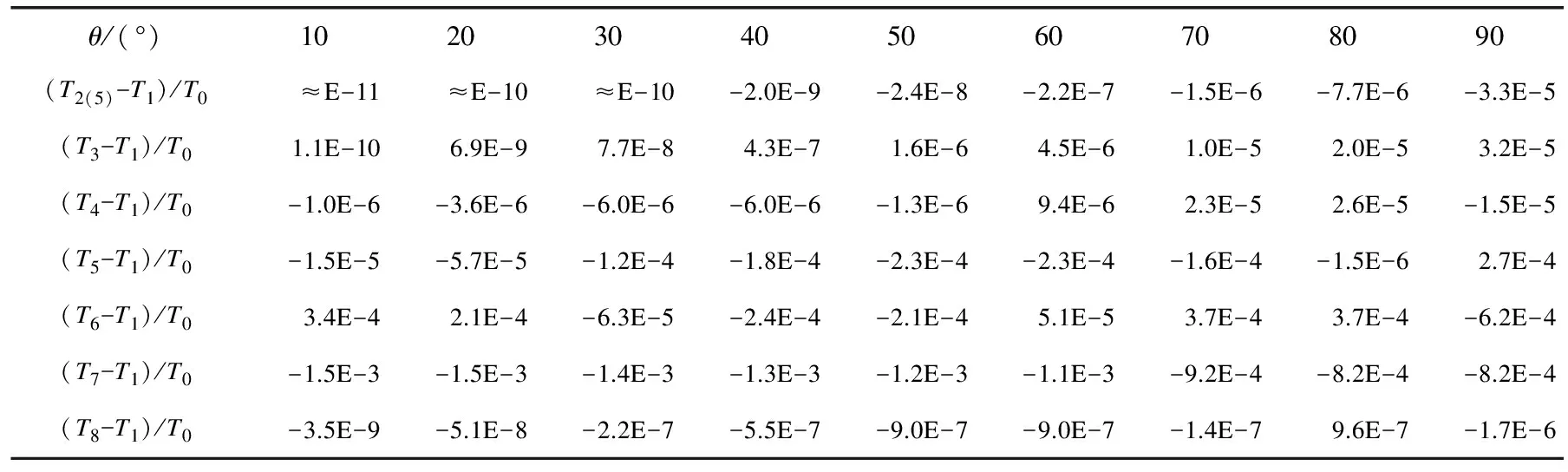
表2 对应摆角θ下各近似表达式的误差与理想单摆周期的比值(Ti-T1)/T0

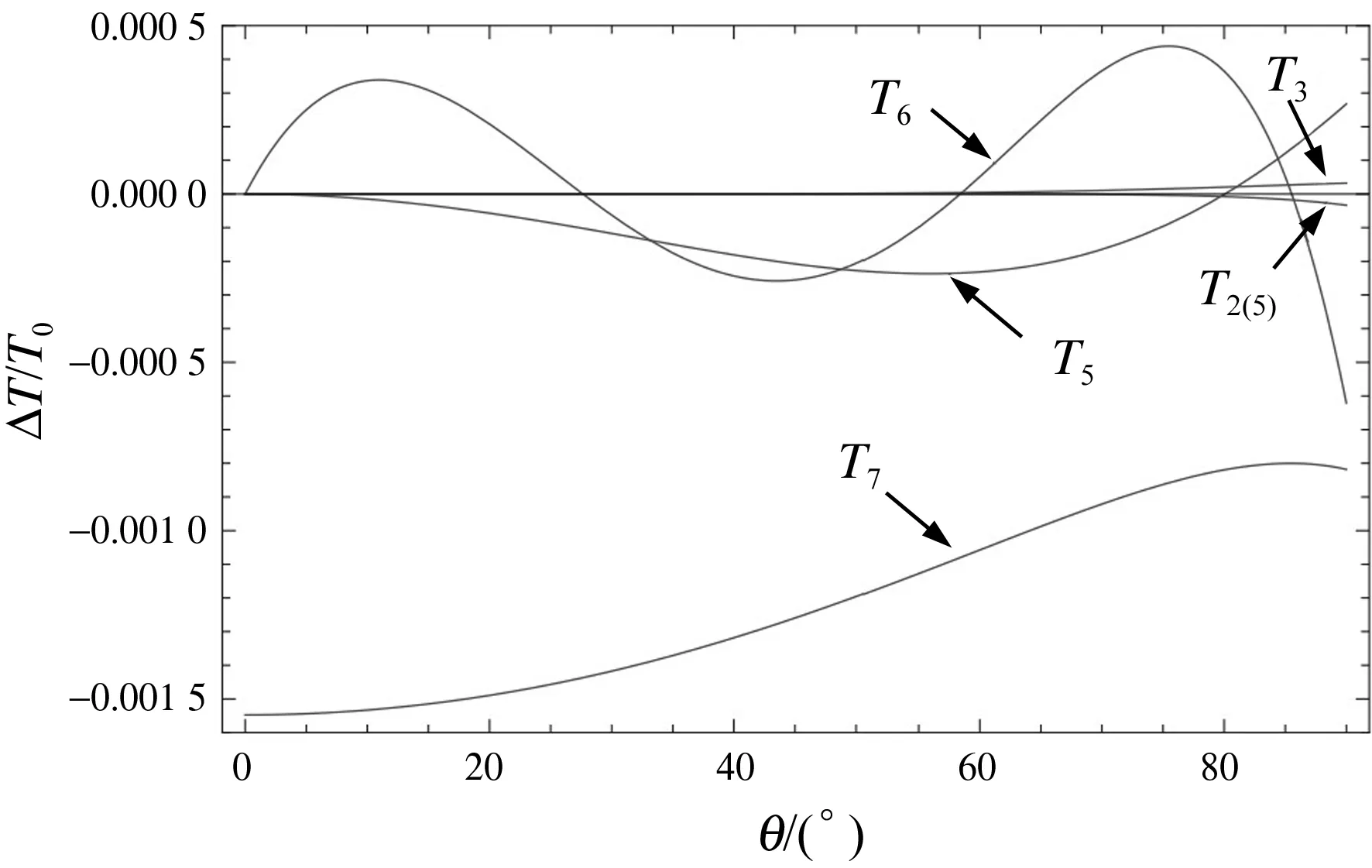
图5 T2(5)、T3、T5、T6、T7的误差曲线比较

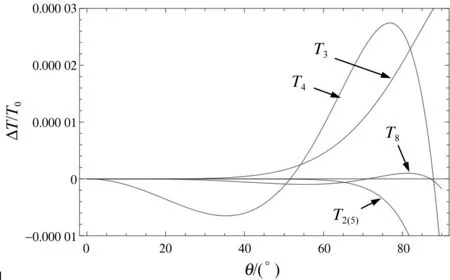
图6 T2(5)、T3、T4、T8的误差曲线比较

考虑到单摆的阻尼和大摆幅修正，式(12)可进一步修改为

(30)

式(30)具有较高的精度，它也可部分转化为有理式，但精度将略有下降，其保留到二级小量的表达式为

(31)

4 结论

根据上述讨论，式(30)具有较高的准确度。鉴于大摆幅单摆的阻尼振动的情况较为复杂，这里不予讨论。依据微小误差独立作用原理，可以确信式(30)用于这种情况的计算也应该具有足够高的准确度。式(30)既有高精度又形式简单，正是我们所需要的近似计算公式。式(31)是保留到二级小量的单摆的各项修正的公式，其精度稍低于式(30)，但也能满足实际应用中的精度需要。

[1]孙丙西.单摆测重力加速度的修正公式[J].内蒙古民族大学学报:自然科学版,2006,20(6):658-659.

[2]郝建明,李咏波,和伟.单摆法测重力加速度的修正公式分析[J].云南师范大学学报：自然科学版,2004,24(3):63-66.

[3]龚善初.影响单摆振动周期的参数研究[J].大学物理,2006,25(6):12-15.

[4]于凤军.单摆系统的振动研究[J].大学物理,2009,28(9):9-12.

[5]于凤军,景义林.一个单摆周期近似公式[J].大学物理,2007,26(5):18-19.

[6]张风雷,鞠衍清.另一个单摆周期近似公式[J].齐齐哈尔大学学报：自然科学版,2008,24(5):76-78.

[7]刘凤祥.单摆运动周期的近似解[J].大学物理,1999,18(11):5-7.

[8]黄兆梁.非线性单摆的精确解与近似解[J].常州工学院学报,1998,11(5):60-62.

[9]鞠衍清,张风雷.单摆运动周期近似公式的数值推导及修正[J].大学物理,2007,26(5):15-17.

[10]袁庆新,曾凡光.对《一个单摆周期近似公式》一文的讨论[J].大学物理,2008,27(9):16-18.

责任编辑：张秀兰

ComprehensiveCorrectionofSimplePendulumPeriodFormula

HUANGZhaoliang

(School of Photoelectric Engineering,Changzhou Institute of Technology,Changzhou 213002)

The equations of motion are derived from the Lagrange function of simple pendulum vibration,resulting in major modifications for the period of simple pendulum,including compound pendulum correction,air buoyancy correction,damping force correction and large amplitude correction.All the corrections are reserved to level two or more.Some mistakes in the simple pendulum correction formula are corrected,and the approximate formula of high precision in large amplitude pendulum conditions is given,so that computing the period of simple pendulum can be more accurate and reliable.

single pendulum;period;nonlinear;large amplitude;correction

2014- 05-20

黄兆梁(1956— )，男，副教授。

1671- 0436(2014)03- 0043- 05