任意摆幅的摆类振动规律研究

朱 平

(普洱学院 理工学院，云南 普洱 665000)



任意摆幅的摆类振动规律研究

朱 平

(普洱学院 理工学院，云南 普洱 665000)

任意摆幅的摆类振动由于涉及椭圆积分，问题的讨论带来一定的困难，通常仅局限于讨论摆角较小时的情况，近似处理为简谐振动.如果不做这种近似处理，对任意的摆幅，摆类的振动规律又如何，振动又有什么特点，是否是简谐振动，这是大学力学教学中学生感到困惑的问题.运用椭圆积分的理论给出了问题的解，并进行了系统、深入的讨论.

任意摆幅;摆类;振动;规律

在力学问题的教学中，单摆、复摆、碗摆、环摆、扭摆等的振动是一类最为基本和重要的振动[1-4]，是研究其他复杂振动的基础.然而，对这类振动的研究，涉及椭圆积分，给问题的讨论带来一定的困难[5-9],一般情况仅局限于讨论摆幅较小时的情况，近似处理为简谐振动.如果不做这种近似处理，对任意的摆幅，这类问题的振动规律又如何，振动又有什么特点，是否是简谐振动，这是大学力学教学中学生感到困惑的问题.下面对这一问题展开分析和讨论.

任意摆幅的单摆、复摆、扭摆以及碗摆等这一类的振动可以简化为通过一刚体的复摆的振动来加以讨论，如图1所示.

一刚体复摆，质量为m,转动惯量为I，过O点的垂直轴为转轴，转轴到质心的距离为d、C为质心，刚体可以绕O的轴自由往复地振动.

当O点为固定点，刚体为集中在C的质点时，为单摆，摆长为d；当过O点的转轴为固定扭体，mg替换为扭摆的内回复力矩，为扭摆；当d为碗的半径，刚体为质量集中于C的半径为r的小球，沿d的方向有碗的支持力，此时为碗摆；当刚体为一环，环上支点为O，环的质量为m，半径为d，为环摆.

研究这一类摆的振动规律，可以先简化为讨论复摆的振动规律，从复摆的振动规律的结果中再使问题具体化得到单摆、扭摆、环摆、碗摆等的具体振动规律.

图1 复摆

1 任意摆幅的复摆

对于一任意摆角φ，复摆受到的回复力矩为-mgdsinφ，由定轴转动定理有

令

则有

对于复摆的振动，有

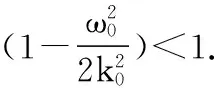
(1)

从微分方程(1)式有

(2)

(2)式为椭圆积分.为得到相应的解对其作变量变换，令

θ.有

于是

(3)

方程(3)为椭圆积分，其解为[10]

(4)

F[θ,k]为第一类椭圆积分函数.从解析式(4)，可以通过计算机数值计算得到角位移随时间的演化规律

φ=G(t)

(5)

(4)或(5)即为任意摆幅的复摆的振动规律的解.

图2 角幅与初角速度的关系

图3 任意摆幅复摆的振动图像

利用复摆微分方程的解析式(4)，通过计算机数值计算的方法，在图3里给出了任意摆幅的复摆振动角位移随时间的演化图φ=G(t).这里，k0=0.7，摆的初角速度ω0取不同的值.从图3看到，任意摆幅的振动是周期函数，但振动的周期和振动的幅度与初角速度有关，在ω0的取值范围里，初角速度越大，振动的幅度越大，周期也越大.显然，振动周期与振动幅度有关，这与简谐振动的周期与摆幅无关是不同的，任意摆幅的复摆的振动不是简谐振动.

于是，可以得到任意摆幅复摆的振动周期解析式[10]

这里，K[k]为第一类完全椭圆积分函数.

图4 单摆的振动周期分布图

图4给出了复摆的振动周期与初角速度ω0、系统固有属性k0间的关系.当初角速度增加，摆幅增大时，系统的周期增大.当初角速度接近系统的限制值(2mgd/I)时，系统的周期迅速增大.在初角速度一定时，系统固有常数k0越大，复摆的振动周期就越小.

如果复摆作sinφ～φ的近似处理，为简谐振动，且

其解为

图5 复摆振动图像与作近似处理

在图5里给出了任意摆幅的复摆振动图像与作近似处理为简谐振动图像的比较.这里，k0=0.5，ω0=0.7.虚线为解析解(4)式给出的任意摆幅的复摆振动图像.实线为复摆作近似处理为简谐振动的振动图像.从图5 看到，当摆角较小时，任意摆幅的振动与作近似处理的简谐振动差别不大，摆角越小，这种一致性就越高.但当时间增加、摆角增大时，复摆实际振动的规律与简谐振动的差别迅速增大.实际复摆的振动周期比近似处理的简谐振动的周期更大，振幅也更大.

图6 振动幅角为3°时复摆振动图像与相应简谐振动图像比较

图6给出了振动幅角为3°时简谐振动图像(实线)与解析式(4)给出的振动图像(实圆点)，这里，ω0=0.7.显然，两者的图像已几乎是重合一致.因此，当幅角较小时，复摆的振动可看作简谐振动.然而，实际的复摆，幅角小于3°的振动不太容易实现，因此，实际的复摆多为非简谐振动，它的振动规律可以由式(4)与式(5)给出.

2 单摆振动规律

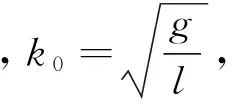
对任意摆幅单摆的振动规律

图7 任意摆幅单摆振动图像与作近似处理的简谐振动图像的比较

图7给出了任意摆幅单摆振动图像与作近似处理的简谐振动图像的比较，这里，k0=0.4，ω0=0.6.从图7看到，单摆任意摆幅的振动与作近似处理的简谐振动的差别比复摆的差别更突出.摆角较小时，一致性较高.但当摆角增大时，单摆实际振动的规律与简谐振动的差别更加突出.单摆实际振动的周期、振幅比简谐振动给出的周期、振幅更大.这是因为单摆作近似处理给出的回复力矩比实际回复力矩更大，所以简谐振动的振幅、周期就更小.周期为

实际单摆的振动周期与复摆的周期有类似的规律，周期与摆幅有关，摆幅越大，周期越大.

3 碗摆的振动规律

碗的半径为R，小球的质量为m, 半径为r，转动惯量为

任意摆幅的碗摆振动规律

周期

显然，系统的固有参数一定时，碗摆的周期与摆幅有关.

图8 碗摆的振动周期与摆球半径关系分布图

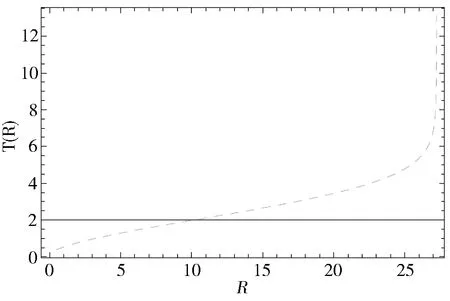
图9 碗摆的振动周期与摆碗半径关系分布图

图8和图9里，ω0=1.2,图8中R=10；图9中r=0.2.在摆幅一定的条件下，碗摆的周期与摆球的半径和摆碗的半径有关，摆球和摆碗的半径越大，碗摆的周期越大.

4 环摆的振动规律

圆环的半径为R，质量为m,转动惯量为

任意摆幅的振动规律

周期

5 扭摆的振动规律

对于扭转轴为理想弹性体的扭摆，当转角为φ时，内回复力矩与扭转角呈线性关系，转动惯量为I,则

c为常数.此时的振动为简谐振动.振动规律

如果扭摆的内回复力矩与扭转角成非线性关系，为非简谐振动.

[1] 漆安慎，杜婵英.力学[M].北京：高等教育出版社，2005.

[2] 梁昆淼.力学[M].北京：人民教育出版社，1978.

[3] 肖士珣.理论力学[M].北京：高等教育出版社，1983.

[4] 郭士堃.理论力学[M].北京：高等教育出版社，1982.

[5] 朱平，赵永达.两体振子问题的研究[J].云南师范大学学报：自然科学版，2003,23(1):25-30.

[6] 朱平.研究椭圆积分物理问题的一种方法[J].大学物理，2003,22(5):25-27.

[7] 朱平.圆电流空间磁场分布[J].大学物理，2005,24(9):13-17.

[8]ZHU P. Field distribution of a uniformly charged circular arc[J]. Journal of Electrostatics,2005, 63(5): 1035-1047.

[9]ZHU P,ZHU Y J.Distributions of potential and field on central axis line generated by elliptic ring uniformly charged[J]. Journal of Electrostatics,2012,70(1):25-30.

[10]BYRD P F,FREDMAN M D.Handbook of ellptic integrals for engineers and physicists[M].second ed.Berlin:Springer-Verlag,1971.

Research on Vibrations of Pendulums for Arbitrary Amplitudes of Angle

ZHU Ping

(School of Science and Technology，Puer Universiy,Puer 665000,China)

Because vibrations of pendulums for arbitrary amplitudes of the angle involve the elliptic integrals,it is difficult to investigate and solve this problem.Usually,the vibration of the amplitude of the angle being smaller is only discussed,which is approximated as a simple harmonic vibration.This paper investigates the problem which makes students feel confused in mechanics teaching and presents the angular displacement function and the period function of pendulums for arbitrary amplitudes of the angle by using the theory of elliptic integrals and the analytic method.

Rbitrary amplitudes of the angle; Pendulums; Vibrations; Law

2014-10-17

朱 平(1958-)，男，云南普洱人，博士，教授，硕士生导师,主要从事大学物理教学方面研究.

朱 平.

O32

A

1007-9793(2015)03-0051-05