具有第二固定负系数星像函数类的相关子集

陈建兰

(南通航运职业技术学院基础教学部，江苏南通226010)

具有第二固定负系数星像函数类的相关子集

陈建兰

(南通航运职业技术学院基础教学部，江苏南通226010)

通过Hadamard积定义了一个分式积分算子Iλ,μ，利用分式积分算子Iλ,μ及固定第二负系数得到了单位开圆内具有第二固定负系数的星像函数类的新子类TSb(λ,μ,α)。文章主要研究了这类新函数类TSb(λ,μ,α)的特征性质。

解析函数；一致凸；星像函数类；第二固定负系数；分式积分算子

O174.51

A

1 问题的提出

近几年来，分式积分算子在解析函数理论中取得了许多有趣的性质和应用。文献[1]～文献[4]中研究了各类分式积分算子定义的解析函数类新子集的包含关系、卷积性质和系数估计等。文章主要研究了一类由分式积分算子定义的具有第二固定负系数的星像函数类相关子集的性质。

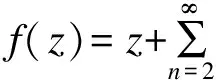
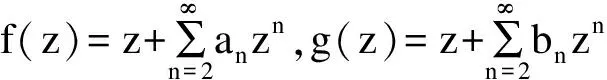
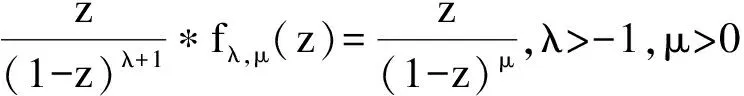
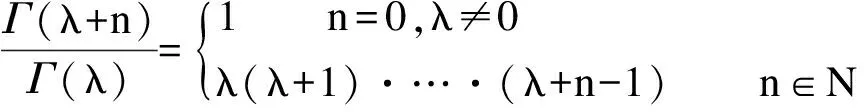
显然，当λ=0,μ=1时，Iλ,μf(z)=f(z)；当λ=0,μ=2时，Iλ,μf(z)=z f′(z)。

利用分式积分算子Iλ,μ定义A的一个新子类Sλ,μ(α)。

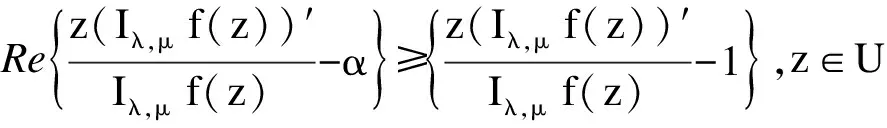
现在定义函数类TS(λ,μ,α)=Sλ,μ(α)∩T。通过固定第二负系数，引入一新子集TSb(λ,μ,α)，定义如下：

定义2 若函数f(z)∈TS(λ,μ,α)且满足

(1)

则称f(z)∈TSb(λ,μ,α)。

本文主要研究了这类具有固定第二负系数函数类的特征性质。

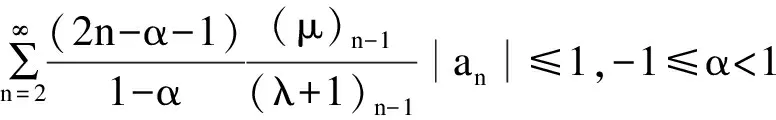
2 主要结论

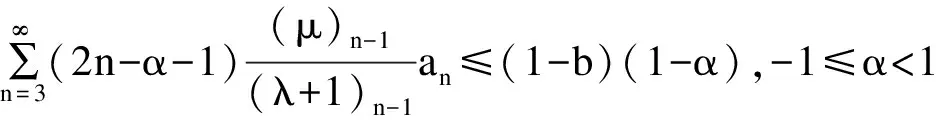
证明因为f(z)∈TS(λ,μ,α)，且an≥0，则由引理1有

(2)

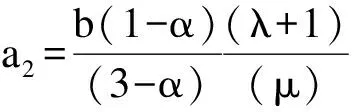
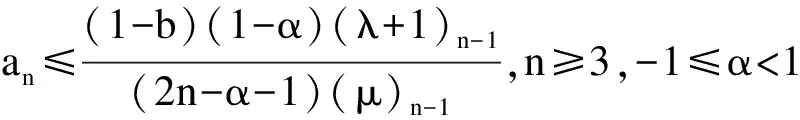
定理2 函数类TSb(λ,μ,α)对凸线性组合封闭。

证明设函数f(z)由式(1)定义，函数g(z)定义如下：

(3)

假设函数f(z)∈TSb(λ,μ,α)，且g(z)∈TSb(λ,μ,α)，定义函数H(z)=σf(z)+(1-σ)g(z)，0≤σ≤1，只需说明函数H(z)∈TSb(λ,μ,α)。

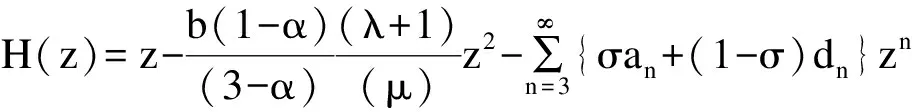
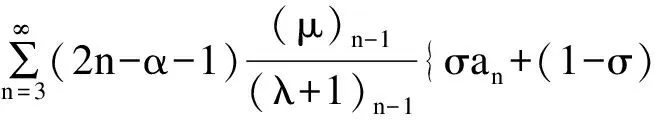
定理3 对每个j(j=1,2,…,m)，函数

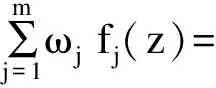
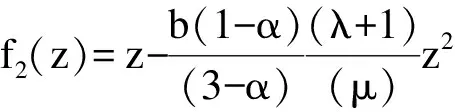
(5)

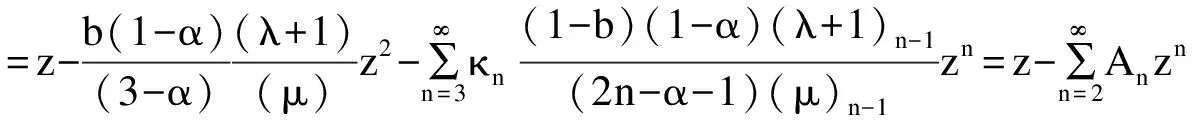
[1]Yang Ding-cong,Liu Jin-lin.On Sakaguchi Functions[J].International Journal of Mathematics and Mathematical Sciences,2003，26(1)：1923-1931.

[2]Liu Jin-lin.Some Applications of Certain Integral Operator[J].KYUNGPOOK Mathematics Journal,2003，43(1)：211-219.

[3]Liu Jin-lin.A linear Operator and Strongly Starlike Functions[J].Journal of Computational and Applied Matematics,2002,54(2)：975-981.

[4]陈建兰，韦叶，刘金林.由算子定义的解析函数的卷积性质[J].扬州大学学报：自然科学版，2006,9(4)：4-6.

[5]Silverman H.Univalent Functions with Negative Coefficients[J].Procject of Amercian Mathematics Socity,1975,51(3)：1091-116.

[6]Nning F R.Integral Representations for Bounded Starlike Functions[J].Computers and Mathematics with Applications,1995,60(2)：289-297.

[7]Liu Jin-lin.Certain Integral Operator and Strongly Starlike Functions[J].International Journal of Mathematics and Mathematical Sciences，2002,30(2) ：569-574.

[8]程艳莉，刘金林.一个线性算子及其相关的亚纯多叶函数类[J].扬州大学学报:自然科学版，2004，7(2)：10-12.

[9]陈建兰.由分式积分算子定义的一致凸函数类的子集[J].盐城工学院学报:自然科学版，2013，26(1)：18-20.

责任编辑：张秀兰

ACorrespondingSubclassofStarlikeFunctionswithFixedSecondNegativeCoefficient

CHENJianlan

(Basic Teaching Department,Nantong Shipping College,Nantong 226010)

Making use of a linear operatorIλ,μ,which is defined here by means of a Hadamard product,we introduce a new classTSb(λ,μ,α) of starlike functions with fixed second negative coefficient defined by using a certain fractional calculus operatorIλ,μ.In this paper,we discuss the characterization property: a necessary and sufficient condition forf(z) to be in the classTSb(λ,μ,α).

analytic functions；uniformly convex；starlike functions；fixed second negative coefficient；fractional calculus operator

2014- 04-30

陈建兰(1981— )，女，硕士，讲师。

1671- 0436(2014)03- 0048- 04